证明函数有界的步骤_「高等数学」证明数列收敛并求该数列的极限，利用单调有界准则...

数列：指的是以正整数集为定义域的函数，是一列有序的数。

极限：某一个函数中的某一个变量，这个变量在变大或者变小的过程中，逐渐向一个确定的数值不断靠近，但是又永远达不到这个数值，那这个数值就会被称作极限值。

而数列恰好是函数，数列极限就是要求出这个数列在变大或者变小的过程中，逐渐靠近的一个确定数值是什么，我们在求数列极限的时候，要转化成函数极限来做。

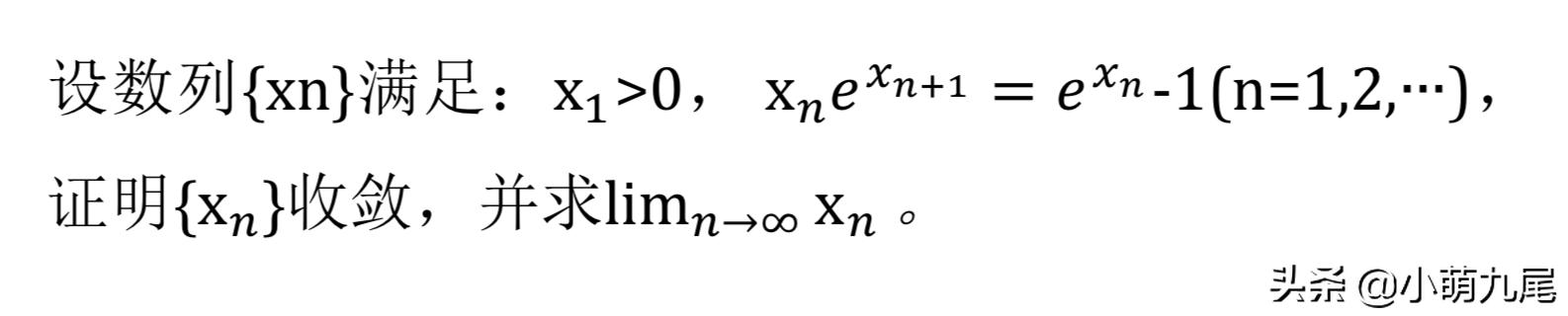
图一

如图所示，我给出这样一道例题，设定一个数列xn，然后相关的条件，证明它收敛，以及这个数列的极限。(证明数列收敛，有时候也只要证明它是一个单调有界的数列，即可直接证明它是一个收敛数列)

拿到题目的时候不要急着做，先对题目进行一个分析。

它说要收敛，也就是证明该数列为收敛数列，想一想对于收敛数列来说，收敛的定义是什么，对于数列而言，如果说存在一个数列{Xn}，而且有一个固定的实数C，如果给出任意的y>0，存在一个正整数N，使得n>N，有Xn-C的绝对值恒小于y，就称作该数列为收敛数列，注意，这里数列的极限就是C，各个点的概念不能够忘记，一定要特别清楚，不清楚的话，即便知道收敛数列的定义也很难做出这道题目了。

图二

我们先根据题目，可以得到哪些信息，千万不要着急。

正如我图中所写的这样，当x>0的时候，我们是不是能够知道e的x次方恒大于1，因为e的零次方刚刚等于零，但是e的x次方是单调递增的。

然后再慢慢一步步进行推导，得到数列{xn}下有界，这里只是证明了它的有界性，那么我们后面的操作就是要证明该数列的单调性，进而证明该数列是单调有界的。

图三

最后给出一个解答方案，由图可知，我们已经证明了该数列的有界性，现在我们要证明它的单调性即可，根据题目给出的条件我们很容易想到用对数的方法来解决，要证明单调性，就是要证明形如xn+1-xn这样的式子恒大于零或者恒小于零，当然，在这道题目中这个式子恒小于零，那么就能够证明该数列是单调递减的，再根据单调有界准则，我们就可以知道该数列收敛，之后再进行求极限就得到a=0。

注意，为什么这个方程两边可以求导，我们可以这样理解，你对方程两边求导，就是对两百年同时除以一个dx，只要dx不等于零，那么方程两边求导后也是相等的，这个一定要注意，因为有很多小伙伴没弄清楚定义域就对方程两边求导，就很容易导致题目做错。

最后做个总结，证明数列是否收敛，以及求该数列的极限的题目的时候，我们要认真分析，用好单调有界准则，用好基本极限的求法，求导也要用好，那么这类题目的难度就不会特别大。