空间三角形_网格参数化原理 - 2：三角形线性映射

现在我们把目光转向三角网格，三角网格不同于我们所说的可微曲面：可微曲面都是

连续，而三角网格只是

连续。

然而，正如同可微曲面在曲面一点P的邻域内有局部线性映射关系（比如参数域上一点(u,v)处的向量映射到3D曲面上则是点(x, y, z)上的曲面切向量，大家可以搜索一下切映射或雅可比矩阵），三角网格上每一个三角单元上也有线性映射关系。我们可以想象：一个3D的三角网格单元，它映射到参数域平面上也应该是一个三角形；每个3D三角形内的一个向量和对应参数域上三角形内的向量之间存在线性关系。

我们可以用下面的图来形象的表示这种线性关系：在UV参数域上的uv等参线映射到3D的三角形平面上依然是平行的等参线。

左图为参数域，右图为3D空间的三角形

下面我们用数学公式推导一下单个3D三角形和参数域上三角形之间的映射关系：

每个三角形从3D到参数域上的映射为

每个3D三角形内的一个向量和对应参数域上三角形内的向量之间存在线性关系，因此在每个三角形内部，

的梯度是常量。

为了简化计算，我们在每个3D的三角形上创建一个局部坐标系，那么三角形的3D坐标

可以转化为局部坐标系上的2D坐标

，我们只需要研究

和

之间的映射关系即可。局部坐标系如下：

设：

设上图中

的参数域坐标为

，三角形内任何一点的参数域坐标为：

其中

是

的重心坐标，根据重心坐标公式（重心坐标理论可以参考

https:// mathworld.wolfram.com/B arycentricCoordinates.html ），重心坐标和XY坐标之间为线性关系：

其中A是三角形的面积：

综合可得：

所以：

同理：

于是

的雅可比矩阵（切映射）为：

多么简洁优美的矩阵公式！

注：这里需要提及的是为啥此处的雅可比矩阵是

和

处在一列而不是一行呢，即：

，为啥不写成更传统的形式

呢？先按书上的内容把它抄下来，不过大家需要注意到这一点。

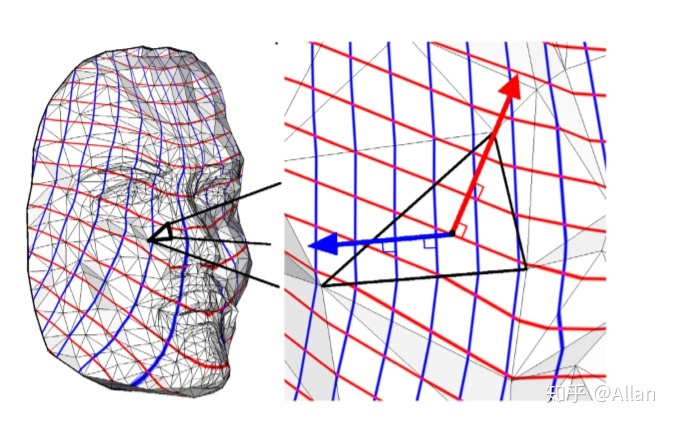
下图是从整体上看3D网格的u-等参线和v-等参线分布，红色箭头是u等参线的梯度矢量，蓝色箭头是v等参线的梯度矢量，它们分别垂直于各自的等参线。

需要提及的是：每条u-等参线和v-等参线是都是一条条的折线，折线的每一段就是一个三角形内部的等参线。三角形和三角形之间的等参线疏密程度不一样，因为每个三角形和参数域之间的切映射并不一样。

3D网格上的等参线是一条一条的折线，折线的每一段都是一个三角形内部的等参线

有了雅可比矩阵，就可以度量3D空间的三角形和参数域空间的三角形之间的变形了！

参考文章：

《Mesh Parameterization: Theory and Practice》