本质矩阵svd分解_矩阵的SVD分解（应用之一：手写数字识别）

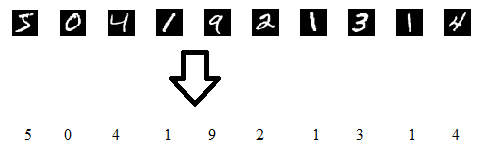
手写字符识别现在是非常常见的，大部分智能手机都支持手写输入。手写字符识别可看作“模式识别”的一个例子，模式识别问题大致可描述为：对于给定的已知数据

与未知数据

构造函数

使输出

有最佳的识别结果。

例如

是含有某个手写数字字符（比如”7“）的灰度图，则模式识别的问题等价于：构造

使

是

所含的那个数字（”7“）。

对于这个问题

的构造是各种各样的，有的有显式表达式（比如基于主成份分析的聚类），而有的并没有（比如深度学习） 。

这里给出一个简单的示例，而且也不打算给出更深入的算法分析，仅为给《线性代数》的学习者一个直观的应用例子。

---

手写字符识别的一些基本假设：

（1）每个手写字符都以一张固定大小（比如

像素）的灰度图像形式存在；

（2）同一个字符的所有手写版本构成一个线性空间（将每个手写字符图像展成一个列向量，这些向量属于某个线性空间，即它是一个线性空间的子集，将子集扩展成一个线性子空间）；

（3）常用字符集中字符个数有限.

---

记

则我们可以把

看作是一个线性空间，为了更便于利用矩阵的性质，可将

改写为

于是我们可以用矩阵

表示

，即

利用矩阵的SVD可知

其中

.

对于给定的

是一个手写数字字符，如果

，则

一定可表示为

的一组基的线性组合，即

（DR-1)

同时

,即

(DR-2)

由于模型本身是近似的，所以有可能式 (DR-1) 的

式也不会为零。但我们有理由相信

如果讨论的字符集是给定的，即

则可令

这等价于求解

个最小二乘问题，但由于我们关心的并不是最小二乘问题的准确解，而只关心最小残差所以不必求出它的全部解。

利用 https://zhuanlan.zhihu.com/p/64273563 所提供的方法，知

---

利用SVD完成手写字符识别的步骤：

1. 利用给定的数据集（训练集）确定
   ;
2. 对每个
   作SVD分解，得到
   ;
3. 确定一个恰当的
   作为空间
   的共同维数；
4. 确定空间
   的一组基
   ；
5. 计算
6. 输出识别结果