向量范数证明例题_第八课：向量的范数

写在前面的话：

很高兴能够认识饭卡里还有好多钱这位土豪大佬。向大佬学习，为成为一名真正的段子手+逗比而奋斗。

范数的概念

向量的范数是一种用来刻画向量大小的一种度量。实数的绝对值，复数的模，三维空间向量的长度，都是抽象范数概念的原型。上述三个对象统一记为

，衡量它们大小的量记为

（我们用单竖线表示绝对值，双竖线表示范数），显然它们满足以下三条性质：

这也是范数的定义，满足上述三条性质的映射我们称之为范数。显然，范数是函数的一种特例。关于三角不等式我们可以通过三角形两边之和大于第三边来理解。

随着以后的学习我们可以知道，长度是范数的一个特例。事实上，二范数对应的就是长度。我们在线性空间中定义内积时，就是把这三条性质作为公理来定义内积的。

我们下面给出向量范数的一些性质：

我们对于第四条性质给出证明。该性质我们可以理解为两边之差小于第三边。

我们下面具体考虑一个范数证明的题：

我们下面就二范数进行证明。

虽然前两个性质貌似是显然的，但是我们并不能这么说，我们现在用数学语言来描述一下。

关于三角不等式的证明需要用到柯西不等式，我们先来讲解一下柯西不等式。柯西不等式说的就是

，这样就把向量的内积和范数联系起来了。

我们在课本24页定义向量的长度的时候是这样定义的：

。现在我们知道，这实际上是二范数的一种表示方式。我们下面给出柯西不等式的证明：

下面结合柯西不等式我们给出三角不等式的证明：

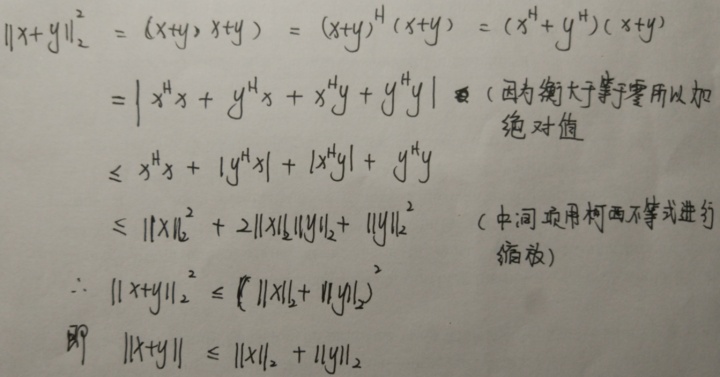
P范数的定义及证明

我们下面来引入更一般的范数定义：

我们要证明他的确是范数需要做诸多的准备工作。在证明过程中就用到了Young不等式和Holder不等式。虽然我们还没有证明，不过我们先引入这个概念和这种记法，因为在接下来的证明过程中会反复的用到。希望大家在看后面的证明过程中不要忘了开头提到的这一点。（就是P范数的定义形式）

我们下面来介绍一下Young不等式，这个不等式的介绍为Holder不等式的证明提供了一个快捷的途径。

该引理（Young不等式）证明如下，其思路就是矩形面积uv不会超过两个曲边梯形面积之和。注意这里会用到了变积分限。对u是在x轴上积分。对v就变成了y轴。

这里我们的曲线公式完全可以写成

，我们应当注意到，积分与符号无关这一点，因此可以写成下图这种形式。

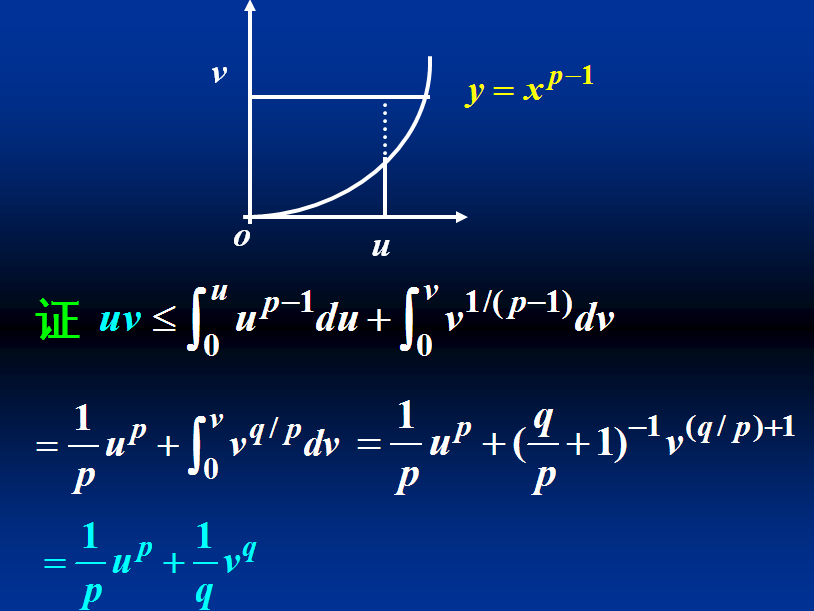
我们有了Young不等式之后，下面来证明Holder不等式。我们首先给出Holder不等式的定义：

下面正面该结论成立：

在这里提醒大家一下，不要忘了开头P范数的定义，因此这里会有:

还记得我们前面说的柯西不等式吗？通过观察Holder不等式其实可以发现，柯西不等式是Holder不等式的一个特例。

（当p和q取2时，结合和的模小于等于模的和所得的结论）

我们给出课本上一道例题：

我们之前只对1范数，2范数和无穷范数进行过证明。我们现在要证明的是如果一个运算，只要满足这个性质。那么它就是一个范数。

下面我们给出证明过程，注意这个证明过程少了正定性和齐次性的证明，只证明了三角不等式。关于正定性和齐次性的证明可以参考之前的证明。

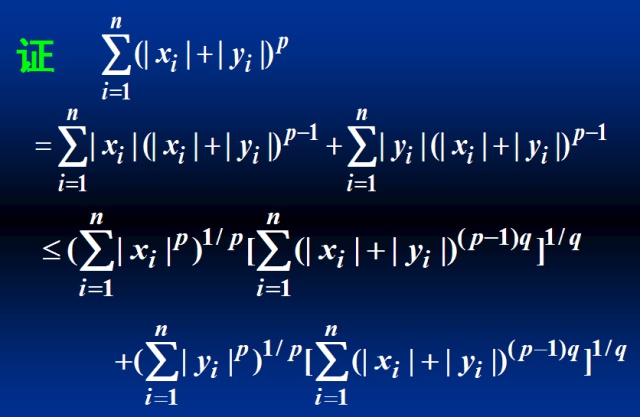
是不是大家已经看晕了，一坨又一坨。接下来的证明写的不是很详细，我写一个更详细的版本。

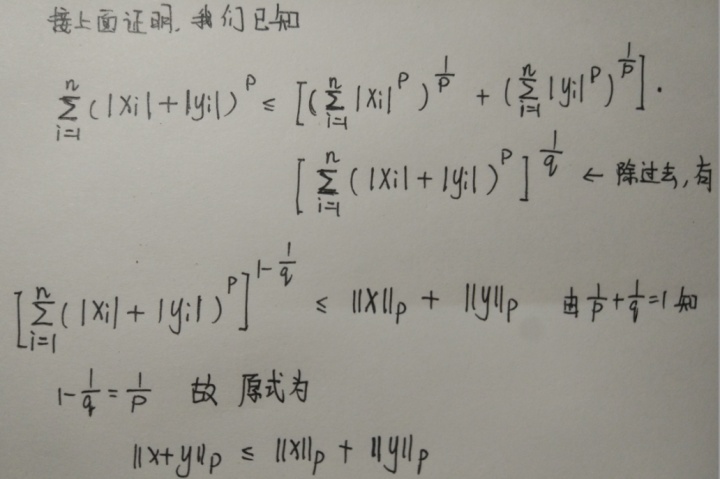
如果忘了，请再次回顾一下P范数的定义。这里特别要注意开P次幂的位置，一定要在中括号的外面。

好了，至此，P范数的证明就全部结束了。好像整个证明过程略微有点长。通过这个证明，P可以取得任意正整数，大大丰富了我们对于如何度量长度的手段，可能有人会问，那P能不能取分数呢？我们现在来说一下：

答案是不行的，只需要举一个反例：

P取1/2，我们知道x+y的P范数是4。而x和y 的P范数都是1。不满足三角不等式，所以不成立。

我们之所以引入范数，为的就是能够在线性空间中进行度量。为了实现这一点，我们有必要引入一个新的概念，这也是这一节啰啰嗦嗦说了半天，想要表达的核心内容。

向量的范数

为了实现在n维空间中的度量，我们必须 将向量的概念和范数进行结合。直接上定理：

这里的

是m维向量范数。A是n维空间中的m×n矩阵。

是n维向量。

证明如下（范数的三条定义）：

实际上这个定理想表达这样一种思想：m维空间中的范数通过矩阵A映射到了n维空间上。有的时候一个空间中的范数我们不好度量，这时候我们可以在另外一个n维空间中进行度量，只需要找到这样的映射矩阵就可以了。

我们下面给出向量序列收敛的定义：

同数列一样，向量也是有好多元素组合而成的，我们将之称为向量序列

。还记得在《高等数学》中我们在定义极限的概念的时候就是从数列极限开始的。类似的，我们这里是从向量序列处定义极限。通过向量序列的收敛性分析我们就从范数的角度给出了极限的定义。

向量存在的充要条件就是n个数列极限存在。

我们下面介绍一下向量范数等价：

向量范数等价是为了解决这样一个问题：我们知道范数有无穷多种（1范数，2范数。。。），同一向量按不同的规定算出的范数一般是不相等的。那么到底按照哪种规则呢？这不就乱了。

范数等价保证了向量序列的收敛性与范数选取无关。无穷范数收敛，其他范数一定收敛。其他范数收敛，无穷范数一定收敛。

我们给出一个定理来具体说明一下：

再给出一个例题：

通过这个例题我们可以看到通过范数来证明收敛的优越性所在，这也是为什么我们有了长度之和还要定义长度的一个原因。

审稿大人辛苦了，这篇文章有点长。