博客聚焦生物医学纵向数据，指出rm - ANOVA和LMEMs在处理非线性数据时的局限性。介绍了GAMs和GAMMs两种处理非线性关系的方法，重点通过数据实战展示了GAM模型的模拟、拟合、评估等过程，包括多个模型的构建与比较，还提及模型选择工作流程及响应条件分布。
目录
前言
之前两篇推文，主要介绍了混合线性效应模型，因为博主是一名临床医生，所以只关注生物医学方面的纵向数据或重复测量数据的分析，在生物医学中，非线性关系广泛存在。
生物医学中的纵向数据
纵向研究旨在重复地测量一组（或多组）受试者中感兴趣的变量，其目的是观察效应随时间的演变，而不是分析单个时间点（例如横断面研究）。生物医学研究经常使用纵向研究来分析“治疗”效应在多个时间点上的演变；在这类研究中，分析对象包括动物（小鼠、大鼠、兔子）、人类患者、细胞或血样等。肿瘤反应、抗体表达和细胞代谢是研究人员使用纵向设计研究一些生理反应的不同情况的示例。由于纵向研究中测量的频率取决于感兴趣的生物现象和研究的实验设计，这类测量的频率可以从分钟间隔来研究动物的麻醉效果，到每周测量来分析中期反应，比如乳腺癌患者皮炎症状的演变，到月度测量以研究长期反应，比如颈部癌症患者放射治疗后的开口情况。
rm-ANOVA和LMEMs的局限性
重复测量方差分析（repeated measures ANOVA 或 rm-ANOVA）可以说是纵向数据的经典分析方法了。rm-ANOVA 模型对纵向数据做出了三个关键假设：1）反应在时间上的线性性，2）同一受试者测量之间的恒定相关性，3）每个受试者的观察结果都在研究期间的所有时间点上获得（这个条件也被称为完全观测）。rm-ANOVA 对时间内预期的线性反应的要求是其中的关键要求。在 rm-ANOVA 中的“线性假设”暗示着当数据不遵循线性趋势时，模型是错误的，导致推论不可靠。在生物医学研究中，纵向研究中的非线性趋势是常态而非例外。一个特定的例子是在临床和临床前设置中研究肿瘤对化疗和/或放疗的反应的数据中出现的这种非线性行为。这些研究表明，所收集的信号并不随时间呈线性趋势，并且在不同时间点表现出极端的变异性，导致 rm-ANOVA 模型的拟合与观察到的变异不一致。因此，当使用 rm-ANOVA 对这类数据进行推断时，估计必然存在偏差，因为该模型只能容纳未能充分代表感兴趣生物现象的线性趋势。与传统的 rm-ANOVA 相比，线性混合效应模型（LMEMs）更加灵活，因为它们可以容纳多个受试者的缺失观测，并允许在每个受试者的每个测量内使用不同的建模策略。然而，LMEMs 对随机效应的误差分布施加了限制，需要它们呈正态分布且独立。更重要的是，LMEMs 也假设反应与时间之间存在线性关系，使其不适合分析非线性数据。
非线性的处理办法
在这里，我介绍两种处理纵向数据非线性关系的方法，包括：Generalized Additive Models（GAMs）和Generalized additive mixed effect models (GAMMs)，两者名字很像，但稍微有点区别和联系。处理纵向数据两种方法都有参考文献支持，并且GAM还可以处理非纵向数据。
GAMs 用于模拟响应变量和预测变量之间的非线性关系。它们通过使用预测变量的平滑函数来灵活表示关系，从而捕捉数据中的非线性模式。当数据呈现复杂的非线性关系，传统线性模型无法充分捕捉时，GAMs特别有用。
另一方面，GAMMs通过纳入随机效应来扩展GAMs，以解释数据中的相关性和异质性。当数据具有分层或聚类结构，例如受试者内的重复测量或组内的测量时，这通常很有用。通过包含随机效应，GAMMs能够同时捕捉固定效应（通过平滑函数进行非线性建模）和随机效应，从而实现对复杂数据结构的更全面建模。
总之，GAMs和GAMMs之间的关键区别在于随机效应的纳入。GAMs使用平滑函数对非线性关系进行建模，而GAMMs通过纳入随机效应来处理相关和分层的数据结构。
数据实战
GAM模型
模拟数据
library(patchwork)
library(tidyverse)
library(mvnfast)
library(nlme)
library(mgcv)
library(gratia)
library(scico)
dat<-tibble(StO2=c(4,27,3,2,0.5,7,4,50,45,56),
Day=rep(c(0,2,5,7,10),times=2),
Group=as.factor(rep(c("Control","Treatment"),each=5))
)
thm1<-scale_fill_scico_d(palette="tokyo",begin=0.3, end=0.8, direction = -1, aesthetics = c("colour","fill"))
#alpha for ribbon
al<-0.8
#subject = factor(paste(subject, treatment, sep = "-")))
n <- 10 #number of observations
sd <- 10 #approximate sd from paper
df <- 6
#calls simulate_data.R to generate simulated responses below
source('D:\\BaiduNetdiskDownload\\nhanes_Rwork\\longtitude\\non_linear_GAM\\GAMs-biomedical-research-main\\scripts\\simulate_data.R')
dat_sim <- simulate_data(dat, n, sd)模拟数据格式如下图。
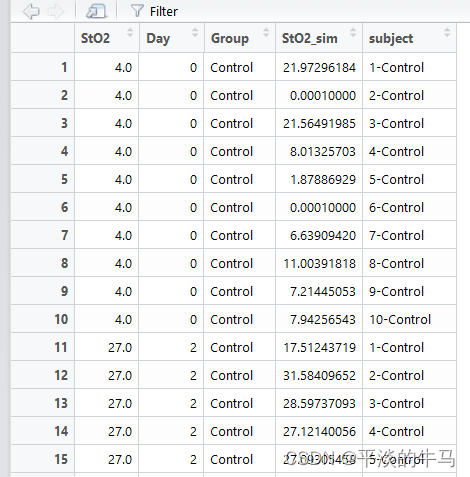
模拟数据作图
#plotting simulated data
f2<-ggplot(dat_sim, aes(x = Day,
y = StO2_sim,
color = Group,
group=subject)) +
geom_point(show.legend=FALSE,
size=1.5,
alpha=0.6)+
geom_line(size=0.6, alpha=0.4,show.legend=FALSE)+
geom_line(aes(x = Day,
y = StO2,
color=Group),
size=1.5,
data=dat,
inherit.aes=FALSE,
show.legend = FALSE)+
labs(y=expression(atop(StO[2],'(simulated)')))+
theme_classic()+
theme(
axis.text=element_text(size=22)
)+
scale_x_continuous(breaks=c(0,2,5,7,10))+
thm1
我们可以看到两组数据都有明显的曲线关系。
拟合GAM模型
下面我们开始一步一步拟合GAM模型，并做出模型评价。
第一个模型
gam_00<-gam(StO2_sim ~ s(Day, k = 5),
method ='REML',
data = dat_sim)对数据拟合的第一个模型是假设治疗组和对照组共享一种随时间变化的单一平滑的模型。模型语法指定gam_00是将包含所有模型信息的对象，并且该模型试图解释StO2_sim（模拟的StO2）随Day的变化。该模型将使用四个基函数（k = 5）进行平滑。默认情况下，该平滑使用薄板回归样条。平滑参数估计方法使用了受限极大似然（REML）。
模型评估
模型诊断使用两种方法：1）图形诊断，2）模型评估。在第一种情况下，可以使用gratia包中的函数appraise和draw来获得所有图形诊断的单一输出。对于模型检查，mgcv包中的函数gam.check和summary提供了关于模型拟合及其参数的详细信息。
图形评估
#see https://patchwork.data-imaginist.com/reference/area.html
layout1 <- c(
area(1, 1),
area( 1, 2),
area(2, 1),
area(2, 2),
area(1, 3, 2)
)
layout2 <- c(
area(1, 1),
area( 1, 2),
area(2, 1),
area(2, 2),
area(1,3,2,5)
)
appr1 <- appraise(gam_00)
sm1 <- draw(gam_00)
visual_check <- appr1 + sm1
visual_check + plot_layout(design = layout1)
第一个GAM模型的图形诊断。左图：来自包_gratia_中的函数appraise提供的图形诊断。右图：模型的拟合平滑，由函数draw提供。
从图一中函数appraise的输出来看，对模型关注的主要指标是残差的QQ图和残差的直方图。QQ图显示误差没有合理地分布在45度线上（表示正态性），因为有多个点偏离了趋势，特别是在尾部。直方图还显示变异性（残差）不符合正态分布的假设。
函数draw允许将平滑绘制为ggplot2对象，如果需要的话，这将方便进行后续操作。由于模型gam_00只指定了一个时间协变量（Day）的平滑，因此绘图只包含一个平滑。需要注意的是，平滑显示出几乎是线性的轮廓。
模型评价
需要特别关注gam.check中的参数'k-index'（它调用k.check进行计算）。该参数指示平滑的基础维度是否足够，即，它检查创建平滑所使用的基础是否足以捕捉数据中的趋势。如果模型未能充分捕捉数据中的趋势，这将通过较低的k-index值（<1）来指示。因为我们稍后使用appraise绘制模型诊断图形，所以通过创建一个自定义函数来抑制gam.check的图形输出，只获取模型估计，从而避免重复进行诊断图形的绘制。这可以通过调用gam.check的源代码，并在新函数中使用适当的代码（将称为gam_diagnostics，可以在脚本gam_diagnostics.R中找到）来实现。
在下一个代码块中，我们调用gam_diagnostics来提供所需的诊断输出：
结果如下：
Method: REML Optimizer: outer newton
full convergence after 5 iterations.
Gradient range [-3.169523e-07,-5.856196e-09]
(score 439.3312 & scale 415.5653).
Hessian positive definite, eigenvalue range [0.05988488,49.00071].
Model rank = 5 / 5
Basis dimension (k) checking results. Low p-value (k-index<1) may
indicate that k is too low, especially if edf is close to k'.
k' edf k-index p-value
s(Day) 4.00 1.37 0.27 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
从gam_diagnostics的输出可以看出，k-index为0.35，表明模型未能捕捉数据中的变异性。edf（有效自由度）是平滑的复杂性指标。在这里，平滑的复杂性与4次多项式相当。接下来，获取拟合模型的摘要，可以通过调用summary来实现。
第二个模型
模型gam_00的一个主要缺陷是它未考虑到数据是分组嵌套的事实。下一个迭代是一个模型，其中在模型语法中使用by = Group，为每个组分配不同的时间（Day）平滑。下面我们拟合这样的模型，保存为gam_01，并使用gam_diagnostiscs来获得模型拟合的信息。
gam_01<-gam(StO2_sim ~ s(Day, by=Group, k = 5),
method ='REML',
data = dat_sim)
gam_diagnostics(gam_01)
summary(gam_01)
#need to add figure number and caption
appr2 <- appraise(gam_01)
sm2 <- draw(gam_01)
visual_check2 <- appr2 + sm2
visual_check2 + plot_layout(design = layout1)Method: REML Optimizer: outer newton
full convergence after 9 iterations.
Gradient range [-9.384614e-09,-1.662737e-11]
(score 407.5399 & scale 193.8685).
Hessian positive definite, eigenvalue range [0.7984408,48.57113].
Model rank = 9 / 9
Basis dimension (k) checking results. Low p-value (k-index<1) may
indicate that k is too low, especially if edf is close to k'.
k' edf k-index p-value
s(Day):GroupControl 4.00 3.44 0.41 <2e-16 ***
s(Day):GroupTreatment 4.00 3.75 0.41 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
R-sq.(adj) = 0.591 Deviance explained = 62.1% -REML = 407.54 Scale est. = 193.87 n = 100
对这个模型的诊断表明，k-指数仍然低于1（从gam_diagnostics的输出为0.58），残差仍未遵循正态分布（图中-GAM-诊断）。此外，平滑曲线（通过draw()函数绘制）的轮廓相当线性，这表明它们仍未捕捉到数据中观察到的趋势。从summary()中得知，模型解释的偏差约为65%。
第三个模型
模型gam_00是出于演示目的建立的，用于涵盖最简单的情况，但它未考虑数据按Group的嵌套结构，这从拟合的平滑类型（单一平滑）、模型诊断以及模型解释的方差较低都可以得知。另一方面，gam_01考虑了每个组内的嵌套情况，并提供了更好的方差解释，为了区分每个组，需要向模型添加一个参数项来描述_Day_和_Group_的交互作用。
这是因为在gam_01中，为每个组分别拟合了平滑曲线，并且这些平滑曲线也试图解释两组响应的不同均值。为Group添加一个参数项使平滑曲线能够捕捉到每个组的时间差异。最终得到的模型是gam_02，这也是主文中拟合的模型。
#GAM for StO2
gam_02 <- gam(StO2_sim ~ Group+s(Day, by = Group, k = 5),
method ='REML',
data = dat_sim)
gam_diagnostics(gam_02)
summary(gam_02)
gam.check(gam_02)
appr3 <- appraise(gam_02)
sm3 <- draw(gam_02)
visual_check3 <- appr3 + sm3
visual_check3 + plot_layout(design = layout2)模型比较
### Comparing models via AIC
AIC(gam_00, gam_01, gam_02) df AIC
gam_00 3.643829 891.6388
gam_01 9.788676 821.5309
gam_02 10.986433 682.4843
拟合曲线
diff_complete <- difference_smooths(gam_02, smooth = "s(Day)",
newdata = newdat,
unconditional = TRUE,
frequentist = FALSE,
n = 100, partial_match = TRUE,
nrep=10000)
my_list <- pairwise_limits(diff_complete)
rib_col <- '#8D7D82' #color for ribbon for confidence interval
control_rib <- '#875F79' #color for ribbon for control region
treat_rib <- '#A7D89E' #color for ribbon treatment region
c1 <- ggplot() +
geom_line(data = diff_complete, aes(x = Day, y = diff),
size = 1, alpha = 0.5) +
annotate("rect", xmin = my_list$init1, xmax = my_list$final1,
ymin = -Inf, ymax = Inf, fill = control_rib,
alpha = 0.5) +
annotate("text", x = 1.5, y = -18, label = "Control>Treatment",
size = 6, angle = 90) +
annotate("rect", xmin = my_list$init2, xmax = my_list$final2,
ymin = -Inf, ymax = Inf, fill = treat_rib,
alpha = 0.5) +
annotate("text", x = 6, y = -18, label = "Treatment>Control",
size = 6, angle = 90) +
geom_ribbon(data = diff_complete,
aes(x = Day, ymin = lower_s, ymax = upper_s),
alpha = 0.5, fill = rib_col, inherit.aes = FALSE) +
geom_hline(yintercept = 0, lty = 2, color = "red") +
scale_x_continuous(breaks = c(0, 2, 5, 7, 10)) +
labs(y = "Difference\n(Complete observations)") +
theme_classic()+
theme(axis.text = element_text(size = 22))
通过平滑置信区间的两两比较可以估计每个治疗组之间的显著差异。
从所选模型（gam_02）中得出的"设计矩阵"（也称为 "Xp 矩阵"）用于计算每个组的平滑项之间的差异的95%置信区间。这种方法可以估计存在显著差异的时间间隔（置信区间在0以上或以下）。默认情况下，在其他软件包（比如G. Simpson的_gratia_）提供的两两比较中并不包括组均值。
因为我们保留了组均值，所以结果图（图中两两比较流程图）显示了平滑项之间的估计差异，以及95%的同时置信区间。值得提醒的是，我们可以直观地看到治疗在第三天开始产生显著影响。随着治疗的进行，影响持续存在，而在第五天的差异幅度（约40%）直接对应了数据中该时间点组的StO2增加的幅度。
使用95%的同时置信区间进行模型gam_02的平滑两两比较，比较包括组均值，因此可以直接相关到响应的大小。阴影区域表示了每个治疗组存在非零效应的时间间隔。
有意思的是，还有其他简单的函数可以对该数据曲线拟合。
library(mgcViz)
gam_fi <- getViz(gam_02)
o <- plot(sm(gam_fi, 1) )
o + l_fitLine(colour = "red") + l_rug(mapping = aes(x=x, y=y), alpha = 0.8) +
l_ciLine(mul = 5, colour = "blue", linetype = 2) +
l_points(shape = 19, size = 1, alpha = 0.1) + theme_classic()
对比一下，可见可信区间扩大了。
在上面过程中展示了GAM的基本模型选择工作流程。目标是让读者熟悉构建每个模型的逻辑和需要检查的诊断信息类型，以确保模型的适用性。最后还需要考虑响应的条件分布。在主要文稿和本工作流程中，我们假设响应呈正态分布，我们认为在许多生物医学场景中这是合适的。然而，我们必须提醒读者，正态分布并不是一种“一刀切”的分布。根据数据类型（计数、二元结果），用户可以在_mgcv_中选择不同的条件分布。
我们还想指出，在R中使用_mgcv_拟合GAM的一个重要优势是，一旦选择了适当的条件分布并对模型诊断进行评估，用户只需要选择一个基础维度（要使用的基础函数的数量），并使用k.check检查基础维度是否充分捕捉了数据的趋势。如果不是这种情况，那么用户需要略微增加k并再次检查k.check。
扫一扫
311
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
