Computational Optimal Transport 笔记——第二章(2)
符号说明
耦合矩阵 coupling matrix: P ∈ R + n × m P \in R^{n \times m}_{+} P∈R+n×m,其中 P i , j P_{i,j} Pi,j代表从 bin i i i 移动到 bin j j j(或者在离散情况下从 x i x_i xi移动到 y j y_j yj)的质量。
Admissible coupling:
(行和为 a a a向量,列和为 b b b向量的矩阵)
L c ( α , β ) \mathcal{L_c}(\alpha, \beta) Lc(α,β) :在离散测度下的 Kantorovich problem。
在任意测度下的 Kantorovich problem
p-Wasserstein distance:
在任意测度中的 p-Wasserstein distance:
2. 理论基础
2.3 Kantorovich Relaxation
Kantorovich
Kantorovich 的核心思想是放松交通的确定性,即一个源点
x
i
x_i
xi只能被分配到另一个点或位置
y
σ
i
y_{\sigma_i}
yσi或者
T
(
x
i
)
T(x_i)
T(xi)。Kantorovich 建议 在任何地点的质量有可能被分配到几个地点。即Kantorovich 不再认为质量运输应该是确定性的,而是考虑一种概率运输,这种概率运输允许质量从一个源头分裂到几个目标。
不是使用排列
σ
\sigma
σ或者 map
T
T
T,而是使用 coupling matix
P
∈
R
+
n
×
m
P \in R^{n \times m}_{+}
P∈R+n×m,其中
P
i
,
j
P_{i,j}
Pi,j代表从 bin
i
i
i 移动到 bin
j
j
j(或者在离散情况下从
x
i
x_i
xi移动到
y
j
y_j
yj)的质量。
Admissible coupling的特征有:
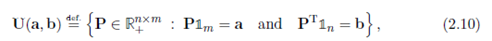
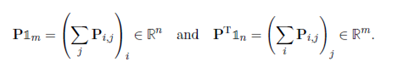
【行和为
a
a
a向量,列和为
b
b
b向量】
可以看出,矩阵集合
U
(
a
,
b
)
U(a,b)
U(a,b)被
n
+
m
n+m
n+m个等式约束,是一个凸多面体。
Kantorovich 的对称性
Kantorovich’s relaxed formulation是对称的,即耦合矩阵
P
P
P在
U
(
a
,
b
)
U(a,b)
U(a,b)中当且仅当
P
T
P^{T}
PT在
U
(
b
,
a
)
U(b,a)
U(b,a)中。
Kantorovich’s optimal transport problem
Kantorovich’s optimal transport problem是
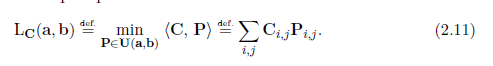
这是一个线性规划问题,与此类程序的通常情况一样,它的最佳解决方案不一定是惟一的。
Remark 2.10 (矿山和工厂)略
Permutation matrices as couplings 对于排列
σ
∈
P
e
r
m
(
n
)
\sigma \in Perm(n)
σ∈Perm(n),我们将对应的排列矩阵
P
σ
P_{\sigma}
Pσ写为
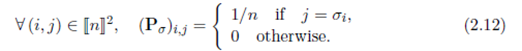
此时有
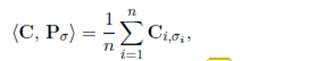
这表明assigment problem可以写为Kantorovich problem,当
P
P
P的约束为排列矩阵:
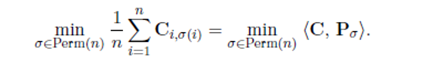
可以计算得,
P
σ
∈
U
(
1
n
n
,
1
n
n
)
P_{\sigma} \in U(\frac{1_n}{n}, \frac{1_n}{n})
Pσ∈U(n1n,n1n),但是不是在
U
(
1
n
n
,
1
n
n
)
U(\frac{1_n}{n}, \frac{1_n}{n})
U(n1n,n1n)中所有的矩阵都是排列矩阵,例如
1
n
1
n
T
/
n
2
1_n 1_n^{T}/n^2
1n1nT/n2。因此
<
C
,
P
>
<C,P>
<C,P>更小
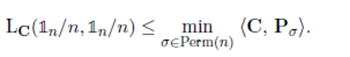
接下来的定理说明两个问题有相同的最小值,也就是说可以找到一个permutation matrix最小化当
a
=
b
=
1
n
/
n
a=b=1_n/n
a=b=1n/n 下 Kantorovich problem。

证明: Brikhoff 理论说明集合
U
(
1
n
/
n
,
1
n
/
n
)
U(1_n/n, 1_n/n)
U(1n/n,1n/n)的极点与 Permutation matrices 是相等的。
Remark 2.11(在离散测度下的 Kantorovich problem)对于离散测度 α , β \alpha,\beta α,β,将于 α , β \alpha, \beta α,β的支撑集中的点两两之间的cost记入矩阵 C C C, C i , j = d e f . c ( x i , y j ) C_{i,j}\xlongequal{def.} c(x_i,y_j) Ci,jdef.c(xi,yj),定义
a , b a,b a,b是支撑集中的概率权重向量。
Remark 2.12(使用 optimal assigments and couplings)OT问题的应用。
可作为阅读文献
Remark 2.13(任意测度下的 Kantorovich problem)在乘积空间上的联合分布中考虑 couplings
在离散测度下
在一般情况下,mass conservation constraint可以被写为联合概率分布下的 marginal constraint
定义投影
P X # P_{\mathcal{X\#}} PX#和 P Y # P_{\mathcal{Y\#}} PY# 是投影的 push-forward。
这些 marginal constraints等价于
Kantorovich问题(2.11)可以一般化为
这是一个在测度空间上的无限维的线性规划问题。如果 ( X , Y ) (\mathcal{X,Y}) (X,Y)是紧空间, c c c是连续函数,这个问题总是有解。

Remark 2.14(概率解释)Kantorovich’s problem可以通过随机变量解释,问题(2.15)可以等价为
其中 ( X , Y ) (X,Y) (X,Y)是在 X × Y \mathcal{X \times Y} X×Y上的随机变量,并且 X ∼ α \mathcal{X}\sim \alpha X∼α, Y ∼ β \mathcal{Y}\sim \beta Y∼β
SUM
2.4 Optimal Transport 的度量性质
OT问题的一个特点就是定义了 histograms (和 probability measures) 之间的距离,要求 cost matrix 满足某些条件。OT问题可以理解为将两点之间的 ground distance 提升到计算 histogram 或 measure 之间的距离。
设 “ground metric” matrix
C
C
C 代表 bin 之间的 cost。我们考虑这种情况 matrix
C
C
C 是固定的,并且在
n
n
n 个 histogram 之间共享。接下来的 Proposition 说明 p-Wasserstein 距离是 histogram 间有效的距离。
Proposition 2.2 我们假设
n
=
m
n=m
n=m,对于一些
p
≥
1
p \geq 1
p≥1,
C
=
D
p
=
(
D
i
,
j
p
)
i
,
j
∈
R
n
×
n
C=D^p=(D_{i,j}^p)_{i,j} \in R^{n \times n}
C=Dp=(Di,jp)i,j∈Rn×n,其中
D
∈
R
+
n
×
n
D \in R^{n \times n}_{+}
D∈R+n×n 是
[
n
]
[n]
[n] 上的距离,即
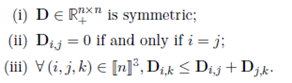
令

定义了在
Σ
n
\Sigma_n
Σn上的 p-Wasserstein distance。可证明
W
p
W_p
Wp是对称、正定、满足三角不等式
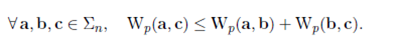
Remark 2.15(在 0 < p ≤ 1 0<p \leq 1 0<p≤1的情况)注意到如果 0 < p ≤ 1 0<p \leq 1 0<p≤1, D p D^{p} Dp是 itself distance。这说明当 p ≥ 1 p \geq 1 p≥1 时, W p ( a , b ) W_{p}(a,b) Wp(a,b)是单纯形 a , b a,b a,b之间的距离。当 p ≤ 1 p \leq 1 p≤1时, W p ( a , b ) p W_p(a,b)^p Wp(a,b)p是纯形 a , b a,b a,b之间的距离。
Remark 2.16(Wasserstein distance 的应用)
Remark 2.17(在测度间的 Wasserstein distance)Proposition 2.2 可以被一般化为处理任意测度。
Proposition 2.3 假设 X = Y , p ≥ 1 , c ( x , y ) = d ( x , y ) p \mathcal{X=Y}, p\geq 1, c(x,y)=d(x,y)^{p} X=Y,p≥1,c(x,y)=d(x,y)p,其中 d d d 是 X \mathcal{X} X上的距离,即
则在 X \mathcal{X} X 上的 p- Wasserstein distance 可以表示为
可证明 W p W_p Wp具有对称、非负和三角不等式
Remark 2.18(几何直觉和弱收敛)Wasserstein距离最重要的一个性质就是它是一个弱距离,即它允许比较支撑集不重叠的奇异分布(例如,离散分布)并量化两个分布之间的空间位移。
在经典的距离(或收敛)不会在离散分布中定义。
鲜明对比的是,对于任何 p > 0 p>0 p>0, W p p ( δ x , δ y ) = d ( x , y ) \mathcal{W_{p}^{p}}(\delta_{x},\delta_{y})=d(x,y) Wpp(δx,δy)=d(x,y)。
注意到 U ( δ x , δ y ) = { δ x , y } \mathcal{U}(\delta_x,\delta_y)=\{\delta_{x,y}\} U(δx,δy)={δx,y},因此Kantorovich问题有唯一可行解, W p p ( δ x , δ y ) \mathcal{W_{p}^{p}}(\delta_{x},\delta_{y}) Wpp(δx,δy),
( d ( x , y ) p ) 1 p = d ( x , y ) (d(x,y)^{p})^{\frac{1}{p}}=d(x,y) (d(x,y)p)p1=d(x,y)。这说明如果 x → y x\to y x→y , W p ( δ x , δ y ) → 0 \mathcal{W_{p}}(\delta_{x},\delta_{y}) \to 0 Wp(δx,δy)→0。这说明 W p \mathcal{W_p} Wp是一种弱收敛的方式。
定义 2.2(弱收敛) X \mathcal{X} X为紧区域,在 M + 1 ( X ) \mathcal{M_{+}^{1}(X)} M+1(X)中 ( α k ) k (\alpha_k)_{k} (αk)k弱收敛于 α \alpha α当且仅当对于任何连续函数 g ∈ C ( X ) g \in \mathcal{C(X)} g∈C(X), ∫ X g d α k → ∫ X g d α \int_{\mathcal{X}} g d\alpha_k \to \int _{\mathcal{X}} g d\alpha ∫Xgdαk→∫Xgdα
记为 α k ⇀ α \alpha_k \rightharpoonup \alpha αk⇀α。
如果对于非紧区域,需要对 g g g加上另外的衰减条件。这个弱收敛的概念对应于随机向量法则中的收敛。
可以证明弱收敛和 W p ( α k , α ) → 0 \mathcal{W_p}(\alpha_k, \alpha) \to 0 Wp(αk,α)→0是等价的。(对于无界度量空间,将矩收敛到p阶。)
Remark 2.19(平移)在欧几里得空间 X = R d \mathcal{X}=R^d X=Rd,ground cost c ( x , y ) = ∥ x − y ∥ 2 c(x,y)=\Vert x-y \Vert^2 c(x,y)=∥x−y∥2 的 Wasserstein distance的特征是可以提出平移因子,令 T τ : x ↦ x − τ T_{\tau}: x \mapsto x-\tau Tτ:x↦x−τ为平移算子,有
W 2 ( T τ # α , T τ ′ # β ) 2 = W 2 ( α , β ) 2 − 2 < τ − τ ′ , m α − m β > + ∥ τ − τ ′ ∥ 2 \mathcal{W}_2(T_{\tau \#}\alpha,T_{\tau' \#}\beta)^2=\mathcal{W_2}(\alpha, \beta)^2-2<\tau-\tau', m_{\alpha}- m_{\beta}>+\Vert \tau-\tau' \Vert^2 W2(Tτ#α,Tτ′#β)2=W2(α,β)2−2<τ−τ′,mα−mβ>+∥τ−τ′∥2
其中 m α = d e f . ∫ X x d α ( x ) ∈ R d m_{\alpha} \xlongequal{def.} \int_{\mathcal{X}} x d\alpha(x) \in R^d mαdef.∫Xxdα(x)∈Rd是 α \alpha α的均值。特别,好的距离的分解为
W 2 ( α , β ) 2 = W 2 ( α ˉ , β ˉ ) 2 + ∥ m α − m β ∥ 2 \mathcal{W_2}(\alpha, \beta)^2= \mathcal{W_2}(\bar{\alpha}, \bar{\beta})^2+\Vert m_{\alpha}-m_{\beta} \Vert^2 W2(α,β)2=W2(αˉ,βˉ)2+∥mα−mβ∥2
其中 ( α ˉ , β ˉ ) (\bar{\alpha},\bar{\beta}) (αˉ,βˉ)是“居中的”零平均度量 α ˉ = T m α # α \bar{\alpha}=T_{m_{\alpha}\#}\alpha αˉ=Tmα#α
Remark 2.20(当 p = + ∞ p=+\infty p=+∞的情况)当 p → + ∞ p \to +\infty p→+∞时 W p p \mathcal{W}_p^p Wpp为
其中 sup 应该理解为在 X 2 \mathcal{X^2} X2 上测度的上确界。
相比于 p < + ∞ p<+\infty p<+∞的情况,这是一个非凸优化问题,难于数值求解和理论研究。 W ∞ \mathcal{W}_{\infty} W∞距离与在 ( α , β ) (\alpha, \beta) (α,β)支撑下的Hausdorff距离有关。
SUM
- p-Wasserstein distance 定义
- 任意测度上p-Wasserstein distance
- p-Wasserstein distance的性质:弱收敛、平移
- W ∞ ( α , β ) W_{\infty}(\alpha, \beta) W∞(α,β)的计算








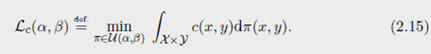

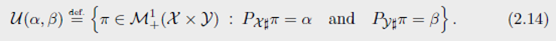

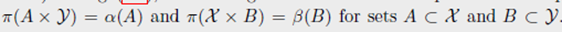

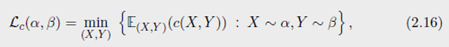


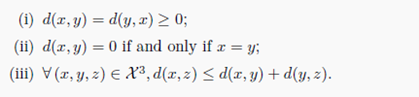
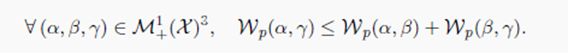
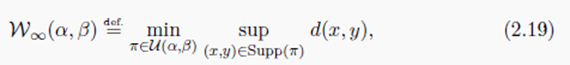














 1191
1191











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








