卷积神经网络CNN(卷积池化、感受野、共享权重和偏置、特征图)

一、前言

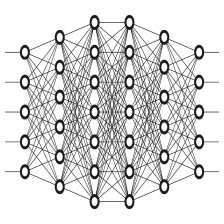
在卷积神经网络(Convolutional Neural Network,CNN)出现之前,神经网络中相邻的所有神经元之间都有连接,这称为全连接(fully-connected),如图1所示

图1 全连接(fully-connected)

 

然而有科学研究,人眼去观察外界时,是通过先观察物体的局部信息,然后通过这些局部信息从而获得全局信息,即识别这个物体是什么.所以根据这个原理去设计神经网络的话,每一个神经元都不需要对全局图像做感受，每个神经元只感受局部的图像区域，然后在更高层，将这些感受不同局部的神经元综合起来就可以得到全局的信息了。显然,这种连接方式大大减少了连接数目,也就是减少了权重参数

这里也就出现了我们经常说的感受野(Receptive Field),即某个神经元能看到的输入图像的区域,关于更多Receptive Field的知识我前面有专栏详细讲解它的理解和计算

玖零猴：感受野(Receptive Field)的理解与计算

 

图2 全连接和局部连接(来自[1])

 

为了加深大家对以上所有过程的认识,我们用图3形象地表达下从全连接到局部连接再到共享权值的过程

 

图3 全连接-局部连接-权值共享

 

二、卷积层

而卷积层就是干了这些事情,每个神经元局部连接上一层的神经元,并且共享权值。

其实, 就是我们经常看到的图4,利用卷积实现了局部连接,然后输出数据里的每个神经元通过同一个卷积核(共享权重)去卷积图像后再加上同一个偏置(共享偏置)得到的,如果没有用共享权值,那么一个神经元需要对应一个卷积核一个偏置,而现在是每个神经元对应的是同一个卷积核同一个偏置,显然参数量大幅下降

 

图4 卷积(来自[2])

 

图5 卷积动图 (图来自[3])

 

有时候还会在​​卷积操作之前向输入数据的周围填充固定的数据(比如0等),这个称为填充(padding),填充为1时,向周围填充一圈,填充为2时,向周围填充两圈.

 

图6 单个卷积核作卷积(来自[2])

 

 

图7 多个卷积核作卷积(来自[2])

 

综上所述, 卷积层不仅大大地减少了参数量,并且还不影响特征的提取

三、池化层

CNN除了新增卷积层外,还新增了池化层,池化(pooling)是用来缩小数据尺寸的运算

在正式讲之前,解释一下特征图(feature map),有时将卷积层或者池化层的输入输出数据称为特征图(feature map),输入数据称为输入特征图(input feature map),输出数据称为输出特征图(output feature map),因此在卷积层中卷积核的数量是等于输出特征图的数量,因为我们知道一个卷积核提取一个特征.

卷积层之后一般是pooling层，池化操作也有一个类似卷积核一样东西在特征图上移动,书[2]中叫它池化窗口,所以这个池化窗口也有大小,移动的时候有步长,池化前也有填充操作,每次移动池化窗口一般要计算的是窗口里的最大值(Max)或者平均值(Average)。

 

图8 Max池化 (来自[2])

 

池化层有三个特征:

1. 没有要学习的参数,这和池化层不同.池化只是从目标区域中取最大值或者平均值,所以没有必要有学习的参数
2. 通道数不发生改变,即不改变feature map的数量
3. 它是利用图像局部相关性的原理，对图像进行子抽样，这样在保留有用信息的,对微小的位置变化具有鲁棒性(健壮), 输入数据发生微小偏差时, 池化仍会返回相同的结果

 

reference

1、理解卷积神经网络CNN中的特征图 feature map

2、《深度学习入门基于Python的理论与实现》

3、卷积动图来源