算例一【拦截导弹(九度教程第95 题)】
-
题目描述

-
解题思路
①最长递增子序列:设f(i)表示L中以a_i为末元素的最长递增子序列的长度,a_j是所有序号在L前面且小于a_i的元素,则有如下的递推方程:
F[1]=1;
F[i]=max{1,F[j]+1 | j<i&&a_j<a_i}
即在求以a_i为末元素的最长递增子序列时,找到元素a_j,即j<i且a_j<a_i
若存在这样的元素,则对所有a_j,都有一个以a_j为末元素的最长递增子序列的长度f(j),把其中最大的f(j)选出来,那么f(i)就等于最大的f(j)加上1,即以a_i为末元素的最长递增子序列,等于以使f(j)最大的那个a_j为末元素的递增子序列最末再加上a_i;
若这样的元素不存在,则递增子序列为1。
②因为后一发导弹不能高于前一发导弹(但是可以相等啊),所以我们要求的是一个不严格下降的递减序列
从左往右按时间顺序求F[i]:
i=1时:F[1]=1;
i>=1且 j<i&&A[j]>=A[i]时:F[i]=max{1,F[j]+1}
-
解题代码
#include<stdio.h>
int main(){
int k;
int h[30];
int num[30];
while(scanf("%d",&k)!=EOF){
for(int i=1;i<=k;i++){
scanf("%d",&h[i]);
}
num[1]=1;
int cnt=num[1];
for(int i=2;i<=k;i++){
int max=1;
for(int j=1;j<i;j++){
if(h[j]>=h[i]){
if(num[j]+1>max)
max=num[j]+1;
}
}
num[i]=max;
if(num[i]>cnt)
cnt=num[i];
}
printf("%d\n",cnt);
}
}-
注意点
①总结其特点:
a)我们将这个问题分割成许多子问题,每个子问题为确定以第i 个数字结束的递增子序列最长长度。
b)这些子问题之间存在某种联系,以任意一个数字结束的递增子序列长度,与以排在该数字之前所有比它小的元素结尾的最长递增子序列长度有关,且仅与其数字量有关,而与其具体排列无关。
c)规模较小的子问题是容易被我们确定的。
于是,我们像递推求解一样,一步步求得每个子问题的答案,进而由这些答案推得后续子问题的答案。
算例二【Coincidence (九度教程第98 题)】
-
题目描述

-
解题思路
①最长公共子序列问题:有两个字符串S1 和S2,求一个最长公共子串,即求字符串S3,它同时为S1 和S2 的子串(不要求连续),且要求它的长度最长,并确定这个长度
②最长公子序列递推公式:
思路参考:here!
-
解题代码
#include <stdio.h>
#include <string.h>
int dp[101][101];
int max(int a,int b) {
return a > b ? a : b; //取最大值函数
}
int main () {
char S1[101],S2[101];
while (scanf ("%s%s" ,S1,S2) != EOF ) { //输入
int L1 = strlen(S1);
int L2 = strlen(S2); //依次求得两个字符串的长度
for (int i = 0; i <= L1; i ++) dp[i][0] = 0;
for (int j = 0; j <= L2 ; j ++) dp[0][ j] = 0; //初始值
for (int i = 1; i <= L1; i ++) {
for (int j = 1; j <= L2 ; j ++) { //二重循环依次求得每个dp[i][j] 值
if (S1[i - 1] != S2[ j - 1]) //因为字符串数组下标从0开始,所以第i个字符位置为S1[i-1],若当前两个字符不相等
dp[i][j] = max(dp[i][j - 1],dp[i - 1][ j]); //dp[i][j] 为dp[i][j - 1] 和dp[i - 1][j] 中较大的一个
else dp[i][j] = dp[ i - 1][ j - 1] + 1; //若它们相等,则dp[i][j]比dp[i - 1][j - 1] 再加一
}
}
printf ("%d\n" ,dp[L1][L2]); //输出答案
}
return 0;
}-
注意点
①总结一下,动态规划问题的时间复杂度由两部分组成:状态数量和状态转移复杂度,往往程序总的复杂度为它们的乘积。









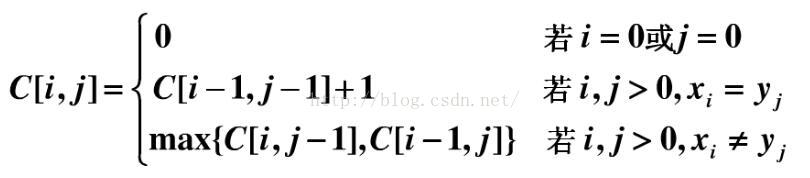














 296
296











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








