论文学习笔记：通用对抗扰动UAP

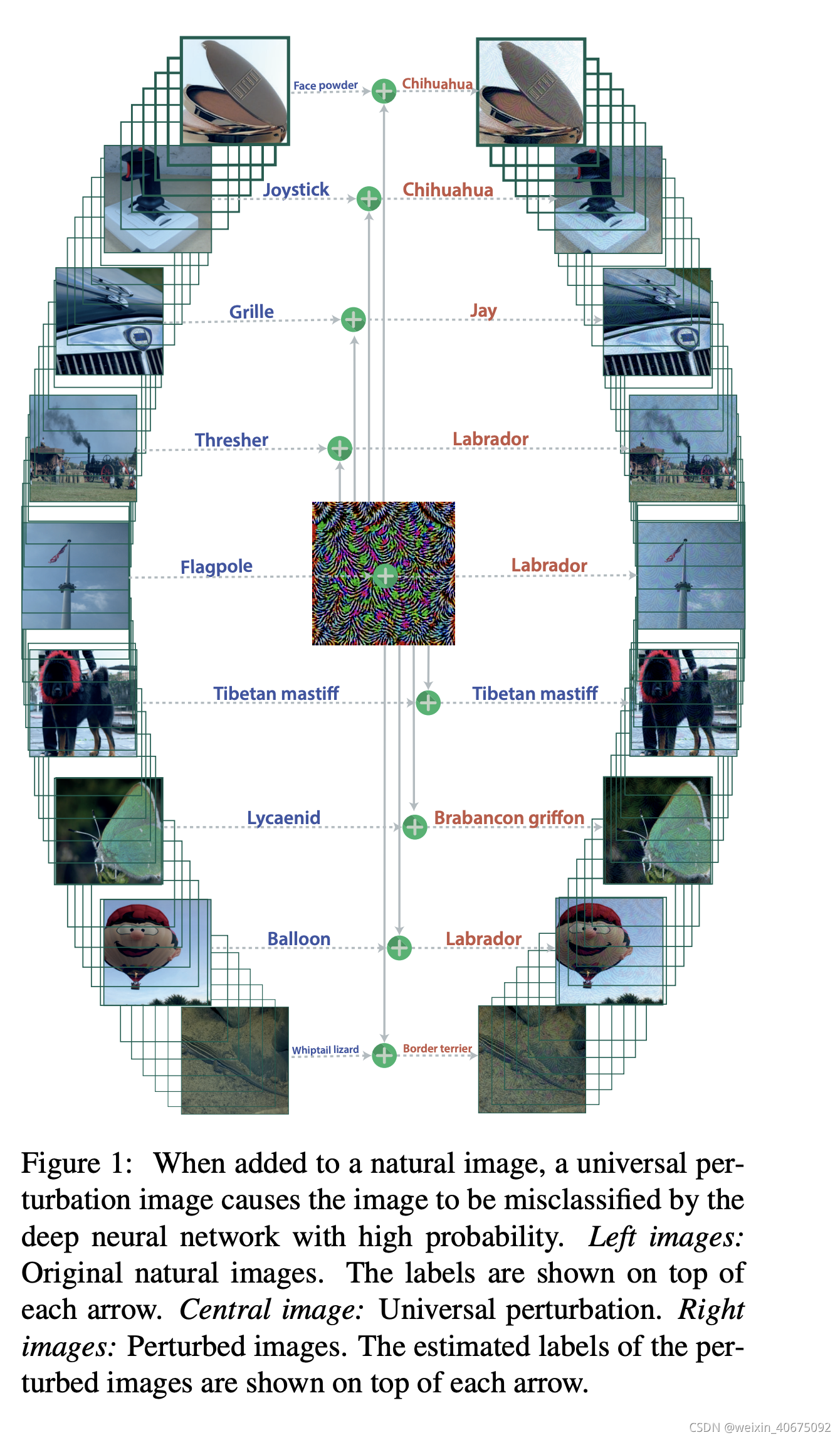
给定一个state-of-the-art的深度神经网络分类器，作者的工作展示了通用对抗扰动(UAP)的存在性，并且提出了计算UAP的方法。经验型的解释了这种扰动，展示了UAP在不同神经网络之间的泛华性。UAP的存在揭示了高维决策边界之间存在重要的几何相关性。进一步概述了现有自然图像分类器存在安全漏洞。

UAP

假设图片$x\in {\mathbb{R}}^d$来自分布$\mu$，注意，这里的$\mu$分布，代表了大部分的自然图片，包含较强的多样性。在这样的情况下，我们要找到通用对抗扰动 $v$，需要$v$满足一下两个条件。

其中，$\xi$表示扰动的幅度，$\delta$表示对分类模型$\hat{k}$的愚弄率。

对于来自$\mu$分布的图像数据点$X$，作者提出了在数据集上迭代，逐步创建通用对抗扰动$v$的方法，在每次迭代计算中，计算将$x+v$推动到分类边界上的最小的$\Delta v_i$。如上图2，数据点$x_1$，$x_2$，$x_3$叠加，3个不同的颜色分别表示不同的分类区域${\mathcal{R}}_1,{\mathcal{R}}_2,{\mathcal{R}}_3$。算法不断计算把当前扰动点$x_i+v$推送到分类边界${\mathcal{R}}_i$的最小扰动，其实也就是到决策边界最小距离(DeepFool)，并把这个最小扰动聚合到当前扰动点上。

详细的讲，假如uap $v$没有在数据点$x_i$愚弄到分类器，计算讲扰动点$x_i+v$推送到分类决策边界的最小扰动$\Delta v_i$（这里是不是很像deepfool），并将KaTeX parse error: Undefined control sequence: \Delata at position 1: \̲D̲e̲l̲a̲t̲a̲ ̲v_i更新到uap $v$上，注意这里的更新并不是简单的加和，为了保持$||v|{|}_p<=\xi$始终成立，将更新后的普遍扰动进一步投影到半径为$\xi$并以 0 为中心的 p 球上。以此来提升uap $v$的愚弄效果。

在添加uap得到数据集 { x 1 + v , x 2 + v , . . . , x n + v } \{x_1 + v, x_2 + v, ..., x_n + v\} {x1​+v,x2​+v,...,xn​+v}，当新生成的数据在分类模型上的”愚弄率“大于阈值$1-\delta$时，算法终止。事实上，并不需要很大的数据$X$来计算在整个$\mu$分布上的图像的uap

值得注意的是，数据集$X$的不同随机组合，会得到不同满足所需约束的uap $v$。所以这个方法可以用来生成多组不同的uap。

实验

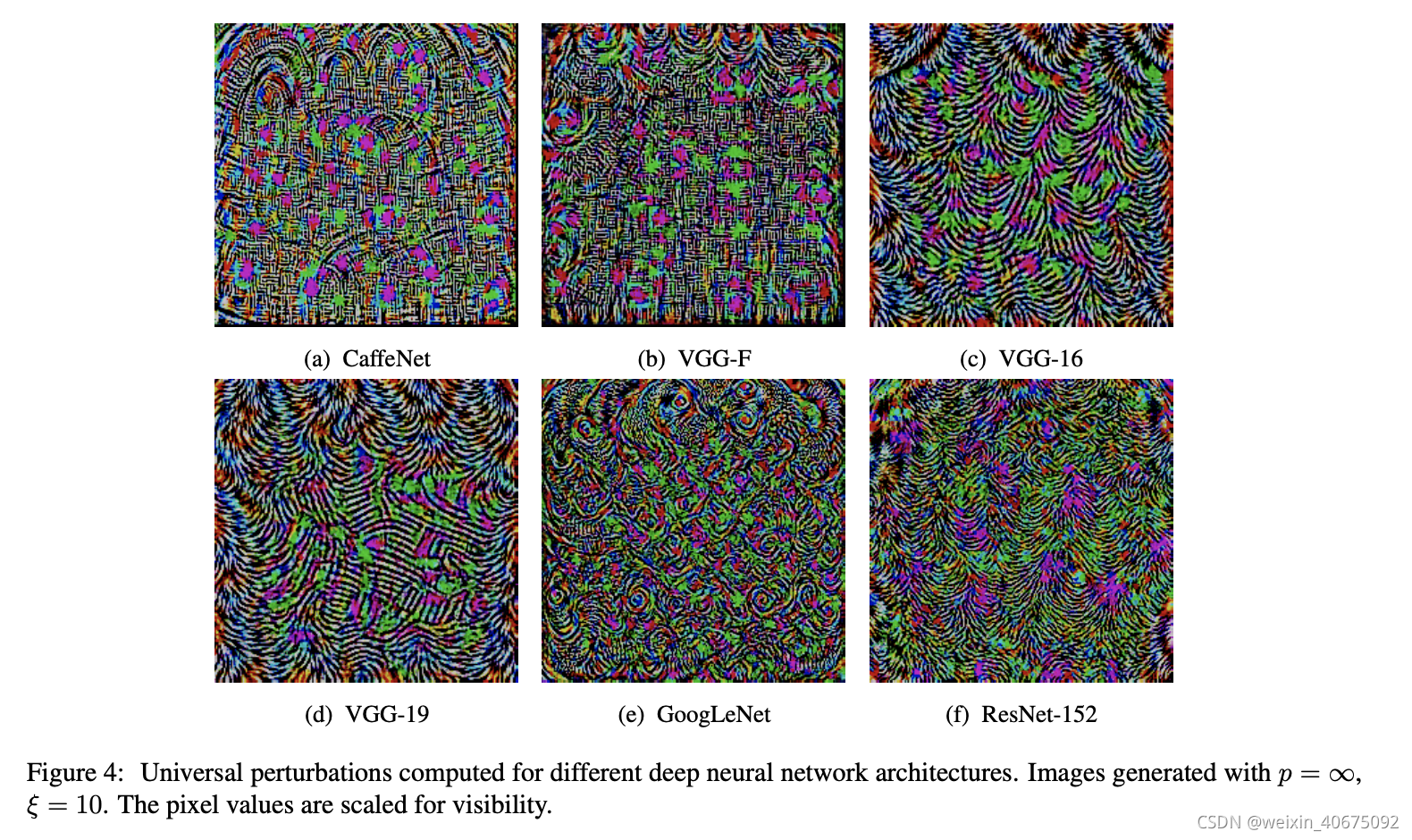
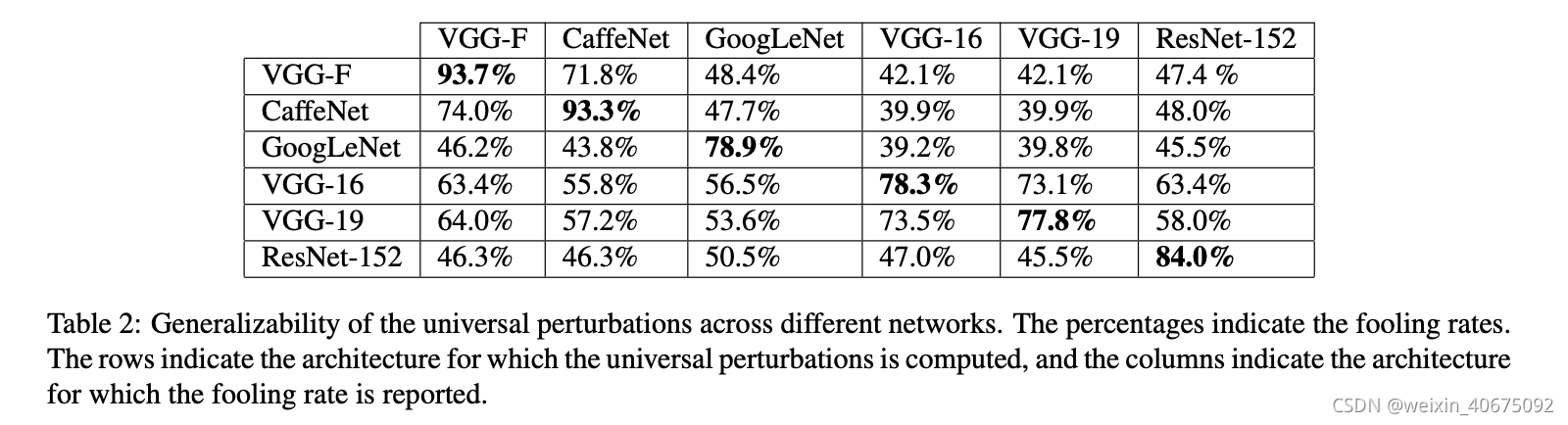
作者设计了不同的实验，Table 1反映了uap在验证集上的fool rate；Figure 4展示了在不同模型结构上计算的uap；Figure 5训练数据集X的shuffle生成的不同uap；Table 2 给出了uap的跨模型泛华性。