分治
MINMAX:
- 普通循环:2n – 2
- 分治 C (n) = 2C (n/2) + 2, n>2 (3n/2 – 2)
- 合并排序:C(n) = 2C(n/2) + n – 1 若n ≥ 2
- 寻找第 k 小元素: 预排序?
- 大整数乘法:
- 矩阵STRASSEN乘法:
减 治
• 插入排序: n2 , n, n2 /4
• 快速排序+插入排序
• 拓扑排序: 减一
• 生成排列+ Johnson-Trotter
- n为偶数: J(2k)=2J(k)-1
- n为奇数: J(2k+1)=2J(k)+1
变治
实例化简:变为同一个问题的更简单的实例
改变表现:
问题规约:变成另一个简单的问题
1 查找出现次数:
蛮力:另外两个表分别存出现的值和频率。(n-1)n/2+(n-1)
模式识别:预排序
动态规划
最短路径:
从后往前:
1 机器负荷分配问题
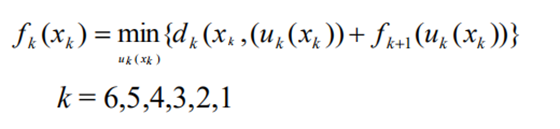
2 排序问题
3 设备更新问题
4 计算二项式系数
C[i,j] ←C[i-1,j-1]+C[i-1,j]
5 最长公共子序列
if ai = bj then L[i, j] ←L[i-1, j-1] + 1
else L[i, j] ←max{ L[i, j-1], L[i-1, j]}
6 0/1 背包问题
- V[i,j] 表示从前i项{u1,u2,…,u*i}中取出来的装入体积为j的背包的价值
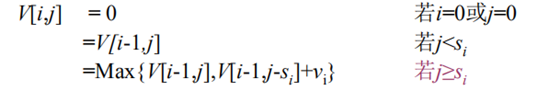
7 最优二叉查找树
8 矩阵链
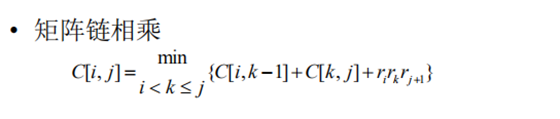
9 最短路径

回溯
着色问题
Tworst =O(n3^n)
n 皇后问题:

贪心
拟阵:




定理 1 拟阵 M 中所有最大独立子集具有相同大小

在一个整数组 A[1…n]中,同时寻找最大值和最小值
输入:n 个整数元素的数组A[1… n], n 为2的幂。
输出:(x, y), A 中的最小元素和最大元素。 • minmax (1, n)
(x1, y1) ← minmax (low, mid)
(x2, y2) ← minmax (mid + 1, high)
x ← min {x1, x2}
y ← max {y1, y2}
= 3n/2 - 2
= logn
寻找第 k 小元素
先排序再直接选择

如果能定义下界,即可使用分支定界算法
下界:城市距离矩阵D 的最小元素乘以城市数量n
稍紧一些的下届:最小的n个元素的和
任何旅行长度l的下届:对于每一个城市i, 1≤i≤n, 求出从城市i到最近的两个城市的距离之和s**i;计算
出这n个数字的和s,并把结果除以2
如果还要包含特定的边:
w9下界

1 最大值最小值确定问题
- 至少 n-1次
- 最坏(3n/2)-2次
2 计算第二大值问题
- Naive algorithm:2n-3
- 淘汰赛:n-1+logn-1
w10优化问题
每个优化问题均伴随着几个判定问题,我们希望找到其中与 优化问题多项式等价的。
1最小顶点覆盖问题
点(或边)的集合,使每一个边(或点)都至少触及一个点(或边)。优化最小的点的集合。
SOL(G) = {};
- 转化成判定问题 :
- P的实例x和K(输入时设置的一个阈值)判定是否m*(x) <=K. 是否存在一个解y, 使m(x,y) <= K(寻找最小时,为了让解小于这个值)
NPO问题:1 实例集I在多项式时间内识别。2 可在多项式q时间内判断实例属于可行解。3 多项式时间内评估。NPO对应的判断问题是NP问题。p.s.最小顶点覆盖问题
PO问题:1问题P是NPO问题。 2 存在多项式时间算法A,对于任意实例x, 算法A返回最优解和最优值。 p.s. 最短路径
- 贪心

方法1与方法2:(以上算法不准。使用一条边中两个端点都加入U,则精确度过大,可能是2近似算法。)
方法3: VCOVERAPPROX 2近似算法
任取一条边,删除和顶点相连的边,没被删除的证明还没被覆盖,和边相连的点就是选择的点。
近似算法
实例 x 的**可行解y, 其值为m(x,y)
实例 x 的最优解 m*(x)
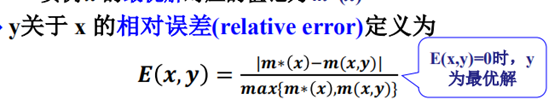
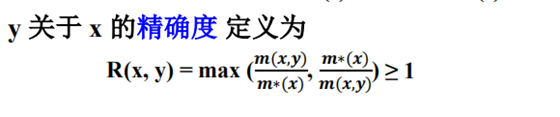






















 7541
7541











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








