几种常用的位置编码介绍及pytorch实现

去追风，去看海

已于 2024-07-29 10:30:45 修改

阅读量2.7k

点赞数 8

分类专栏： NLP 文章标签： python NLP

于 2024-07-29 10:23:04 首次发布

本文链接：https://blog.csdn.net/weixin_40959890/article/details/140764045

版权

NLP 专栏收录该内容

104 篇文章

订阅专栏

引言

我借给你300块与你借给我300块具有完全不同的含义。对于Transformer模型来说，由于Attention模块的无序性(无法区分不同位置的Token)，必须加入额外的信息来记录顺序，这里引入了位置编码。
位置编码从实现方式上大致可以分为2类:

绝对位置编码: 将位置信息融入到输入中
相对位置编码: 微调Attention结构，使其可以分辨不同位置的Token

1，绝对位置编码

1.1 正弦和余弦位置编码（Sinusoidal Positional Encoding）

这种方法通过正弦和余弦函数为每个位置生成一个唯一的向量。这种编码方法的一个优点是它不依赖于具体的序列长度。
在这里插入图片描述

PyTorch实现 1：

class SinPositionEncoding(nn.Module):
    def __init__(self, max_sequence_length, d_model, base=10000):
        super().__init__()
        self.max_sequence_length = max_sequence_length
        self.d_model = d_model
        self.base = base

    def forward(self):
        pe = torch.zeros(self.max_sequence_length, self.d_model, dtype=torch.float)  # size(max_sequence_length, d_model)
        exp_1 = torch.arange(self.d_model // 2, dtype=torch.float)  # 初始化一半维度，sin位置编码的维度被分为了两部分
        exp_value = exp_1 / (self.d_model / 2)

        alpha = 1 / (self.base ** exp_value)  # size(dmodel/2)
        out = torch.arange(self.max_sequence_length, dtype=torch.float)[:, None] @ alpha[None, :]  # size(max_sequence_length, d_model/2)
        embedding_sin = torch.sin(out)
        embedding_cos = torch.cos(out)

        pe[:, 0::2] = embedding_sin  # 奇数位置设置为sin
        pe[:, 1::2] = embedding_cos  # 偶数位置设置为cos
        return pe

SinPositionEncoding(d_model=4, max_sequence_length=10, base=10000).forward()

正弦位置编码不需要进行学习，是初始化时直接根据如上公式赋值的常量, 因此有一定的外推性。又由于位置 $\alpha+\beta$ 的向量可以表示成位置α和位置β的向量组合，表明正弦编码可以表达相对位置信息。

PyTorch实现 2：

import torch
import math

class SinusoidalPositionalEncoding(torch.nn.Module):
    def __init__(self, d_model, max_len=5000):
        """
        正弦和余弦位置编码初始化
        :param d_model: 模型的维度
        :param max_len: 序列的最大长度
        """
        super(SinusoidalPositionalEncoding, self).__init__()
        
        # 初始化一个形状为 (max_len, d_model) 的位置编码矩阵
        pe = torch.zeros(max_len, d_model)
        # 生成一个形状为 (max_len, 1) 的位置索引矩阵
        position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
        # 根据公式计算div_term
        div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
        
        # 对位置矩阵的偶数位置填充sin值
        pe[:, 0::2] = torch.sin(position * div_term)
        # 对位置矩阵的奇数位置填充cos值
        pe[:, 1::2] = torch.cos(position * div_term)
        
        # 在第0维增加一维，然后转置，使其形状为 (1, max_len, d_model)
        pe = pe.unsqueeze(0).transpose(0, 1)
        # 将pe注册为buffer，表示它不是模型的参数，而是模型的一部分，不会在训练中更新
        self.register_buffer('pe', pe)

    def forward(self, x):
        # 将位置编码加到输入张量上
        return x + self.pe[:x.size(0), :]

# 示例使用
d_model = 512
max_len = 100
pos_encoding = SinusoidalPositionalEncoding(d_model, max_len)
sample_input = torch.zeros(max_len, 1, d_model)
output = pos_encoding(sample_input)
print(output.shape)  # torch.Size([100, 1, 512])

1.2 可学习的位置编码（Learnable Positional Encoding）

可学习的位置编码通过直接为每个位置学习一个向量。这种方法需要额外的参数，但能更灵活地适应具体任务。
这种位置编码是Bert、GPT、ViT等架构的实现方式，直接将位置编码当作可训练参数，让它随着训练过程更新。实现方式简单，交给模型进行自学习，大力出奇迹。

PyTorch实现 1：

class TrainablePositionEncoding(nn.Module):
    def __init__(self, max_sequence_length, d_model):
        super().__init__()
        self.max_sequence_length = max_sequence_length
        self.d_model = d_model

    def forward(self):
        pe = nn.Embedding(self.max_sequence_length, self.d_model)
        nn.init.constant(pe.weight, 0.)
        return pe

PyTorch实现 2：

import torch
import torch.nn as nn

class LearnablePositionalEncoding(nn.Module):
    def __init__(self, d_model, max_len=5000):
        """
        可学习的位置编码初始化
        :param d_model: 模型的维度
        :param max_len: 序列的最大长度
        """
        super(LearnablePositionalEncoding, self).__init__()
        # 创建一个Embedding层，形状为 (max_len, d_model)
        self.position_embeddings = nn.Embedding(max_len, d_model)

    def forward(self, x):
        # 获取输入序列的长度
        seq_len = x.size(0)
        # 生成位置索引，形状为 (seq_len, 1)
        position_ids = torch.arange(seq_len, dtype=torch.long, device=x.device).unsqueeze(1)
        # 将位置索引通过Embedding层转换为位置编码，然后加到输入张量上
        return x + self.position_embeddings(position_ids)

# 示例使用
d_model = 512
max_len = 100
pos_encoding = LearnablePositionalEncoding(d_model, max_len)
sample_input = torch.zeros(max_len, 1, d_model)
output = pos_encoding(sample_input)
print(output.shape)  # torch.Size([100, 1, 512])

2，相对位置编码（Relative Positional Encoding）

相对位置编码旨在解决绝对位置编码在捕捉相对位置关系上的局限性。相对位置编码在Transformer模型中应用广泛，特别是在语言模型中。
相对位置并没有完整建模每个输入的位置信息，而是根据Attention中K,V矩阵的偏移量产生不同的Embedding，计算Attention时考虑当前位置与被Attention位置的相对距离。相对位置编码几乎都是在Softmax之前的Attention矩阵上进行操作的

2.1 经典相对位置编码

相对位置编码起源于Google的论文《Self-Attention with Relative Position Representations》，华为开源的NEZHA模型也用到了这种位置编码。

PyTorch实现 1：

class RelativePosition(nn.Module):
    def __init__(self, num_units, max_relative_position):
        super().__init__()
        self.num_units = num_units
        self.max_relative_position = max_relative_position
        self.embeddings_table = nn.Parameter(torch.Tensor(max_relative_position * 2 + 1, num_units))
        nn.init.xavier_uniform_(self.embeddings_table)

    def forward(self, length_q, length_k):
        range_vec_q = torch.arange(length_q)
        range_vec_k = torch.arange(length_k)
        distance_mat = range_vec_k[None, :] - range_vec_q[:, None]
        distance_mat_clipped = torch.clamp(distance_mat, -self.max_relative_position, self.max_relative_position)
        final_mat = distance_mat_clipped + self.max_relative_position
        final_mat = torch.LongTensor(final_mat).cuda()
        embeddings = self.embeddings_table[final_mat].cuda()

        return embeddings

class RelativeMultiHeadAttention(nn.Module):
    def __init__(self, d_model, n_heads, dropout=0.1, batch_size=6):
        "Take in model size and number of heads."
        super(RelativeMultiHeadAttention, self).__init__()
        self.d_model = d_model
        self.n_heads = n_heads
        self.batch_size = batch_size

        assert d_model % n_heads == 0
        self.head_dim = d_model // n_heads

        self.linears = _get_clones(nn.Linear(d_model, d_model), 4)
        self.dropout = nn.Dropout(p=dropout)
        self.relative_position_k = RelativePosition(self.head_dim, max_relative_position=16)
        self.relative_position_v = RelativePosition(self.head_dim, max_relative_position=16)

        self.scale = torch.sqrt(torch.FloatTensor([self.head_dim])).cuda()

    def forward(self, query, key, value):
        # embedding
        # query, key, value = [batch_size, len, hid_dim]
        query, key, value = [l(x).view(self.batch_size, -1, self.d_model) for l, x in
                             zip(self.linears, (query, key, value))]

        len_k = query.shape[1]
        len_q = query.shape[1]
        len_v = value.shape[1]

        # Self-Attention
        # r_q1, r_k1 = [batch_size, len, n_heads, head_dim]
        r_q1 = query.view(self.batch_size, -1, self.n_heads, self.head_dim).permute(0, 2, 1, 3)
        r_k1 = key.view(self.batch_size, -1, self.n_heads, self.head_dim).permute(0, 2, 1, 3)
        attn1 = torch.matmul(r_q1, r_k1.permute(0, 1, 3, 2))

        r_q2 = query.permute(1, 0, 2).contiguous().view(len_q, self.batch_size * self.n_heads, self.head_dim)
        r_k2 = self.relative_position_k(len_q, len_k)
        attn2 = torch.matmul(r_q2, r_k2.transpose(1, 2)).transpose(0, 1)
        attn2 = attn2.contiguous().view(self.batch_size, self.n_heads, len_q, len_k)
        attn = (attn1 + attn2) / self.scale

        attn = self.dropout(torch.softmax(attn, dim=-1))
        # attn = [batch_size, n_heads, len, len]
        r_v1 = value.view(self.batch_size, -1, self.n_heads, self.head_dim).permute(0, 2, 1, 3)
        weight1 = torch.matmul(attn, r_v1)
        r_v2 = self.relative_position_v(len_q, len_v)
        weight2 = attn.permute(2, 0, 1, 3).contiguous().view(len_q, self.batch_size * self.n_heads, len_k)
        weight2 = torch.matmul(weight2, r_v2)
        weight2 = weight2.transpose(0, 1).contiguous().view(self.batch_size, self.n_heads, len_q, self.head_dim)

        x = weight1 + weight2
        # x = [batch size, n heads, query len, head dim]

        x = x.permute(0, 2, 1, 3).contiguous()
        # x = [batch size, query len, n heads, head dim]

        x = x.view(self.batch_size * len_q, self.d_model)
        # x = [batch size * query len, hid dim]

        return self.linears[-1](x)

PyTorch实现 2：

import torch
import torch.nn as nn

class RelativePositionalEncoding(nn.Module):
    def __init__(self, d_model, max_len=5000):
        """
        相对位置编码初始化
        :param d_model: 模型的维度
        :param max_len: 序列的最大长度
        """
        super(RelativePositionalEncoding, self).__init__()
        # 创建一个Embedding层，形状为 (2 * max_len - 1, d_model)
        self.relative_position_embeddings = nn.Embedding(2 * max_len - 1, d_model)
        self.max_len = max_len

    def forward(self, x):
        # 获取输入序列的长度
        seq_len = x.size(0)
        # 生成位置索引，形状为 (seq_len,)
        positions = torch.arange(seq_len, dtype=torch.long, device=x.device)
        # 计算相对位置索引，形状为 (seq_len, seq_len)
        relative_positions = positions[:, None] - positions[None, :] + self.max_len - 1
        # 将相对位置索引通过Embedding层转换为相对位置编码
        relative_position_embeddings = self.relative_position_embeddings(relative_positions)
        return relative_position_embeddings

# 示例使用
d_model = 512
max_len = 100
pos_encoding = RelativePositionalEncoding(d_model, max_len)
sample_input = torch.zeros(max_len, 1, d_model)
output = pos_encoding(sample_input)
print(output.shape)  # torch.Size([100, 100, 512])

2.2 旋转位置编码

在Llama及Llama2，QWen等模型中，使用了这种位置编码的方式。在论文RoFormer: Enhanced Transformer with Rotary Position Embedding中有详细的解释。 Rope是将绝对位置编码与相对位置编码进行结合，通过绝对位置编码的方式实现相对位置编码。
在这里插入图片描述
旋转位置编码通过将位置编码引入到注意力机制的每一个键和值的向量中，从而实现位置编码。这种方法在自回归模型中应用广泛，特别是在提高模型的长序列建模能力上。

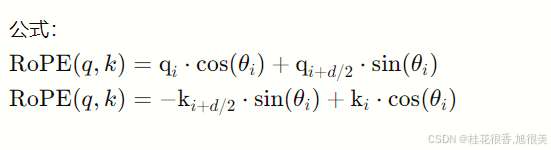
Rope有不同的实现方式，这里是Llama源码中的实现:

PyTorch实现 1：

# 生成旋转矩阵
def precompute_freqs_cis(dim: int, seq_len: int, theta: float = 10000.0):
    # 计算词向量元素两两分组之后，每组元素对应的旋转角度\theta_i
    freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
    # 生成 token 序列索引 t = [0, 1,..., seq_len-1]
    t = torch.arange(seq_len, device=freqs.device)
    # freqs.shape = [seq_len, dim // 2] 
    freqs = torch.outer(t, freqs).float()  # 计算m * \theta

    # 计算结果是个复数向量
    # 假设 freqs = [x, y]
    # 则 freqs_cis = [cos(x) + sin(x)i, cos(y) + sin(y)i]
    freqs_cis = torch.polar(torch.ones_like(freqs), freqs) 
    return freqs_cis

# 旋转位置编码计算
def apply_rotary_emb(
    xq: torch.Tensor,
    xk: torch.Tensor,
    freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
    # xq.shape = [batch_size, seq_len, dim]
    # xq_.shape = [batch_size, seq_len, dim // 2, 2]
    xq_ = xq.float().reshape(*xq.shape[:-1], -1, 2)
    xk_ = xk.float().reshape(*xk.shape[:-1], -1, 2)

    # 转为复数域
    xq_ = torch.view_as_complex(xq_)
    xk_ = torch.view_as_complex(xk_)

    # 应用旋转操作，然后将结果转回实数域
    # xq_out.shape = [batch_size, seq_len, dim]
    xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(2)
    xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(2)
    return xq_out.type_as(xq), xk_out.type_as(xk)

class Attention(nn.Module):
    def __init__(self, args: ModelArgs):
        super().__init__()

        self.wq = Linear(...)
        self.wk = Linear(...)
        self.wv = Linear(...)

        self.freqs_cis = precompute_freqs_cis(dim, max_seq_len * 2)

    def forward(self, x: torch.Tensor):
        bsz, seqlen, _ = x.shape
        xq, xk, xv = self.wq(x), self.wk(x), self.wv(x)

        xq = xq.view(batch_size, seq_len, dim)
        xk = xk.view(batch_size, seq_len, dim)
        xv = xv.view(batch_size, seq_len, dim)

        # attention 操作之前，应用旋转位置编码
        xq, xk = apply_rotary_emb(xq, xk, freqs_cis=freqs_cis)

        # scores.shape = (bs, seqlen, seqlen)
        scores = torch.matmul(xq, xk.transpose(1, 2)) / math.sqrt(dim)
        scores = F.softmax(scores.float(), dim=-1)
        output = torch.matmul(scores, xv)  # (batch_size, seq_len, dim)

PyTorch实现 2：

import torch
import math

class RotaryPositionalEncoding(torch.nn.Module):
    def __init__(self, d_model, max_len=5000):
        """
        旋转位置编码初始化
        :param d_model: 模型的维度，必须为偶数
        :param max_len: 序列的最大长度
        """
        super(RotaryPositionalEncoding, self).__init__()
        self.d_model = d_model
        self.max_len = max_len

        # 计算旋转角度theta
        theta = torch.arange(0, d_model, 2, dtype=torch.float32)
        theta = theta / d_model * math.pi  # 缩放因子
        self.theta = torch.exp(-theta)  # 计算最终的theta值

    def forward(self, q, k):
        """
        前向传播
        :param q: 查询向量，形状为 (batch_size, seq_len, d_model)
        :param k: 键向量，形状为 (batch_size, seq_len, d_model)
        :return: 旋转位置编码后的查询和键向量
        """
        # 获取输入张量的大小
        seq_len = q.size(1)

        # 生成位置索引
        position_ids = torch.arange(seq_len, dtype=torch.float32, device=q.device)
        position_ids = position_ids.unsqueeze(1)  # 增加一个维度

        # 计算旋转位置编码
        angle = position_ids * self.theta
        sin_angle = torch.sin(angle)
        cos_angle = torch.cos(angle)

        # 将查询和键向量分成两部分
        q1, q2 = q[..., :self.d_model//2], q[..., self.d_model//2:]
        k1, k2 = k[..., :self.d_model//2], k[..., self.d_model//2:]

        # 计算旋转位置编码后的查询和键向量
        q_rot = torch.cat([q1 * cos_angle - q2 * sin_angle, q1 * sin_angle + q2 * cos_angle], dim=-1)
        k_rot = torch.cat([k1 * cos_angle - k2 * sin_angle, k1 * sin_angle + k2 * cos_angle], dim=-1)

        return q_rot, k_rot

# 示例使用
d_model = 512
max_len = 100
pos_encoding = RotaryPositionalEncoding(d_model, max_len)
sample_q = torch.randn(1, max_len, d_model)
sample_k = torch.randn(1, max_len, d_model)
output_q, output_k = pos_encoding(sample_q, sample_k)
print(output_q.shape, output_k.shape)  # torch.Size([1, 100, 512]) torch.Size([1, 100, 512])