个人博客地址 Glooow,欢迎光临~~~
文章目录
1. 传统集合的定义
论域 U,集合 A,这可以用一个映射来表示
χ
A
:
U
→
{
0
,
1
}
u
↦
χ
A
(
u
)
\begin{aligned} \chi_{A}: \boldsymbol{U} \rightarrow &\{\mathbf{0}, \mathbf{1}\} \\ \boldsymbol{u} \mapsto & \chi_{A}(\boldsymbol{u}) \end{aligned}
χA:U→u↦{0,1}χA(u)
也可以用一个分段函数来表示
χ
A
(
u
)
=
{
1
,
u
∈
A
0
,
u
∉
A
\chi_{A}(u)=\left\{\begin{array}{ll} {1,} & {u \in A} \\ {0,} & {u \notin A} \end{array}\right.
χA(u)={1,0,u∈Au∈/A

2. 模糊集合的定义
模糊集的含义表示其中的元素
x
x
x “有一定的可能性”属于集合
A
A
A,或者说“一定程度上”属于集合
A
A
A,那么这个属于的程度就被称为隶属度
μ
A
(
x
)
∈
[
0
,
1
]
\mu_A(x)\in [0,1]
μA(x)∈[0,1]。与传统集合相比,传统集合中元素的隶属程度非 0 即 1,也即要么属于,要么不属于,是确定的,模糊集里则引入了一定的不确定性。也用一个映射表示为
μ
A
:
U
→
[
0
,
1
]
x
↦
μ
A
(
x
)
∈
[
0
,
1
]
\begin{aligned} \mu_{A}: &\boldsymbol{U} \rightarrow[0,1] \\ &\boldsymbol{x} \mapsto \mu_{A}(x) \in[0,1] \end{aligned}
μA:U→[0,1]x↦μA(x)∈[0,1]
其中映射
μ
A
\mu_A
μA 称为
A
A
A 的隶属函数,
μ
A
(
x
)
\mu_A(x)
μA(x) 为
x
x
x 对
A
A
A 的隶属度。注意
μ
A
(
x
)
=
0.5
\mu_A(x)=0.5
μA(x)=0.5 时表示最具有模糊性。
3. 模糊集的表示方法
3.1 Zadeh 表示法
A = A ( x 1 ) x 1 + A ( x 2 ) x 2 + ⋯ + A ( x n ) x n A=\frac{A\left(x_{1}\right)}{x_{1}}+\frac{A\left(x_{2}\right)}{x_{2}}+\cdots+\frac{A\left(x_{n}\right)}{x_{n}} A=x1A(x1)+x2A(x2)+⋯+xnA(xn)
这里
A
(
x
i
)
x
i
\frac{A\left(x_{i}\right)}{x_{i}}
xiA(xi) 表示
x
i
x_i
xi 对模糊集
A
A
A 的隶属度为
A
(
x
i
)
A(x_i)
A(xi)。若论域
U
U
U 为无限集,则模糊集表示为
A
=
∫
x
∈
U
A
(
x
)
x
A=\int_{x\in U} \frac{A(x)}{x}
A=∫x∈UxA(x)
3.2 序偶表示法
A = { ( x 1 , A ( x 1 ) ) , ( x 2 , A ( x 2 ) ) , ⋯ , ( x n , A ( x n ) ) } A=\left\{\left(x_{1}, A\left(x_{1}\right)\right),\left(x_{2}, A\left(x_{2}\right)\right), \cdots,\left(x_{n}, A\left(x_{n}\right)\right)\right\} A={(x1,A(x1)),(x2,A(x2)),⋯,(xn,A(xn))}
3.3 向量表示法
A = ( A ( x 1 ) , . . . , A ( x n ) ) A=(A(x_1),...,A(x_n)) A=(A(x1),...,A(xn))
4. 模糊集的运算
4.1 集合基本运算
- 相等: A = B ⟺ A ( x ) = B ( x ) , ∀ x ∈ U A=B \iff A(x)=B(x), \forall x\in U A=B⟺A(x)=B(x),∀x∈U
- 包含: A ⊂ B ⟺ A ( x ) ≤ B ( x ) , ∀ x ∈ U A\subset B \iff A(x)\le B(x), \forall x\in U A⊂B⟺A(x)≤B(x),∀x∈U
- 交集: ( A ∩ B ) ( x ) = A ( x ) ∧ B ( x ) , ∀ x ∈ U (A\cap B)(x) = A(x)\wedge B(x),\forall x\in U (A∩B)(x)=A(x)∧B(x),∀x∈U
- 并集: ( A ∪ B ) ( x ) = A ( x ) ∨ B ( x ) , ∀ x ∈ U (A\cup B)(x) = A(x)\vee B(x),\forall x\in U (A∪B)(x)=A(x)∨B(x),∀x∈U
- 补集: A c ( x ) = 1 − A ( x ) , ∀ x ∈ U A^c(x)=1-A(x),\forall x\in U Ac(x)=1−A(x),∀x∈U
其中记号 a ∧ b = min { a , b } , a ∨ b = max { a , b } a\wedge b=\min\{a,b\},a\vee b=\max\{a,b\} a∧b=min{a,b},a∨b=max{a,b}
4.2 计算性质
很多计算性质都和普通集合差不多


需要注意的是无穷个集合的交集与并集的定义
⋃
t
∈
T
A
t
(
a
)
=
sup
t
∈
T
A
t
(
a
)
⋂
t
∈
T
A
t
(
a
)
=
inf
t
∈
T
A
t
(
a
)
\bigcup_{t \in T} A_{t}(a)=\sup_{t \in T} A_{t}(a) \\ \bigcap_{t \in T} A_{t}(a)=\inf_{t \in T} A_{t}(a)
t∈T⋃At(a)=t∈TsupAt(a)t∈T⋂At(a)=t∈TinfAt(a)
5. 隶属度的确定
5.1 实验统计法
5.2 (半)解析法
根据问题性质套用现有模糊分布,然后根据测量数据确定分布中的参数。
模糊分布大致分为:偏大型、偏小型、中间型
5.3 专家打分法
根据专家的反馈意见进行统计
6. 截集与分解定理
6.1 截集的定义
定义:若
A
A
A 为
U
U
U 上的任一模糊集,对
∀
λ
∈
[
0
,
1
]
\forall \lambda\in [0,1]
∀λ∈[0,1],记
A
λ
=
{
x
∣
A
(
x
)
≥
λ
,
x
∈
U
}
A_\lambda = \{x|A(x)\ge\lambda,x\in U\}
Aλ={x∣A(x)≥λ,x∈U}
称为
A
A
A 的**
λ
\lambda
λ-截集**,其中
λ
\lambda
λ 称为阈值或置信水平。类似的,**强截集(开截集)**定义为
A
λ
=
{
x
∣
A
(
x
)
>
λ
,
x
∈
U
}
A_\lambda = \{x|A(x)>\lambda,x\in U\}
Aλ={x∣A(x)>λ,x∈U}
注意:截集为普通集合,不是模糊集!
6.2 截集运算性质
大部分性质都很简单

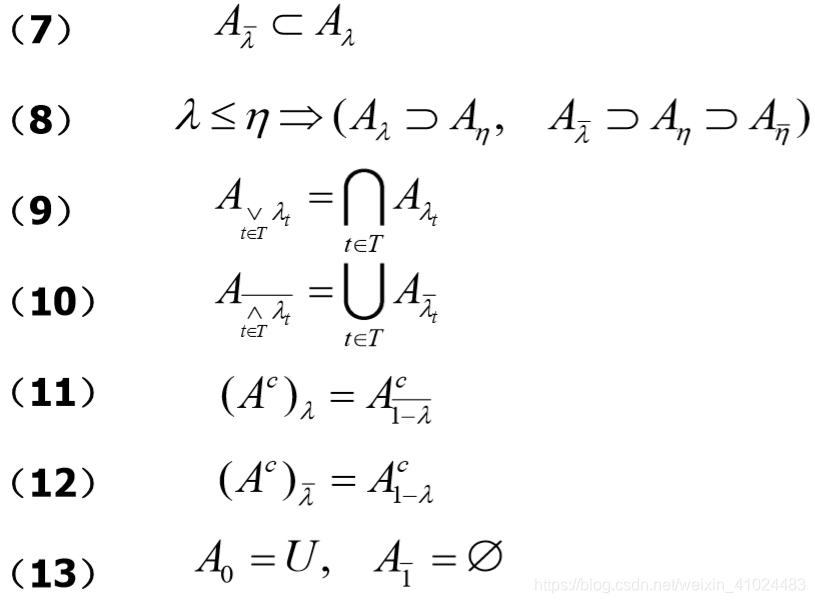
但注意其中第 3 和第 6 条注意并不是相等!!
6.3 一些定义
- 核: k e r ( A ) = A 1 ker(A)=A_1 ker(A)=A1
- 支集: s u p p ( A ) = A 0 ˉ supp(A)=A_{\bar{0}} supp(A)=A0ˉ
- 边界: A 0 ˉ \ A 1 A_{\bar{0}}\backslash A_1 A0ˉ\A1
- 数乘:
λ
A
(
u
)
=
λ
∧
A
(
u
)
,
u
∈
U
\lambda A(u) = \lambda \wedge A(u),u\in U
λA(u)=λ∧A(u),u∈U
- A ⊂ B ⇒ λ A ⊂ λ B A\subset B \Rightarrow \lambda A \subset \lambda B A⊂B⇒λA⊂λB
- λ 1 ≤ λ 2 ⇒ λ 1 A ⊂ λ 2 A \lambda_1\le\lambda_2\Rightarrow \lambda_1 A \subset \lambda_2 A λ1≤λ2⇒λ1A⊂λ2A
6.4 分解定理
分解定理 1: A ∈ F ( U ) A\in \mathcal{F}(U) A∈F(U),则 A = ⋃ λ ∈ [ 0 , 1 ] λ A λ A=\bigcup_{\lambda\in[0,1]}\lambda A_\lambda A=⋃λ∈[0,1]λAλ
分解定理 2: A ∈ F ( U ) A\in \mathcal{F}(U) A∈F(U),则
























 1181
1181

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








