半导体制冷片（TEC）参数与性能曲线应用指南

谢谢～谢先生

于 2025-04-27 08:45:00 发布

阅读量793

点赞数 27

分类专栏：电路应用文章标签：硬件工程嵌入式硬件

本文链接：https://blog.csdn.net/weixin_41226265/article/details/132562057

版权

电路应用专栏收录该内容

84 篇文章

订阅专栏

半导体制冷片参数

1. 引言

半导体制冷片（Thermoelectric Cooler, TEC）的性能评估和选型依赖于其性能曲线。本文通过具体案例，详细说明如何利用制冷量（Qc）、输入电压（Vin）、制冷效率（COP）等参数的函数关系图，设计满足特定需求的制冷系统。

Qc vs I曲线：用于确定工作电流和制冷能力。
Vin vs I曲线：用于计算输入功率和电源需求。
COP vs I曲线：用于优化能效，降低能耗。

2. 性能曲线的使用方法示例

2.1 制冷量Qc与输入电流I的关系

例如我们有一个小型电子“黑匣子”正在释放25W的热量。为了保证电子元件正常工作，其温度不应该超过20 ℃。室温一般是20 ℃左右，因此需要使用热电制冷器来降低元件的温度。

127对TEC的Qc vs I曲线

图.1：127对TEC的Qc vs I曲线（DT=30℃）。

上图所示，这幅图描述了制冷器的制冷量Qc、温差ΔT与输入电流I的函数关系。在这个例子中，建立起热电制冷器的工作参数Th=50 ℃, Tc=20 ℃, Qc=25 w。所需的温差是ΔT=30 ℃。

案例背景：

需要冷却的电子“黑匣子”发热量：25 W
允许的元件最高温度：20℃
环境温度：20℃
假设散热器温度（Th）为50℃（最坏情况）
选择制冷器型号：127对温差电偶，最大额定电流6 A

步骤解析：

确定温差DT：
- 温差DT = Th - Tc = 50℃ - 20℃ = 30℃。
查找Qc最大值点（A点）：
- 在图9.1（Qc vs I曲线）中，找到DT=30℃的曲线。
- 当输入电流I=6 A时，该曲线的Qc最大值为36 W（略高于需求的25 W）。
调整至目标制冷量（B点）：
- 沿DT=30℃曲线向下移动，找到Qc=25 W对应的点B。
- 从B点向x轴投影，得到此时的输入电流为3.0 A。
关键点说明：
- A点（6 A, 36 W）表示制冷器在最大电流下的制冷能力。
- B点（3.0 A, 25 W）是满足需求的最优工作点，此时输入电流较低，能效更高。

2.2 输入电压Vin与输入电流I的关系

下图所示描述了制冷器的输入电压Vin、温差DT与输入电流I的函数关系。在这个例子中，热电制冷器的工作参数包括Th=50 ℃, Tc=20 ℃, I=3.0 A。

案例参数：

Th=50℃，Tc=20℃，目标电流I=3.0 A

127对温差电偶，6安培制冷器输入电压Vin、温差DT与输入电流I的函数关系

图.2：127对TEC的Vin vs I曲线（DT=30℃）。

步骤解析：

定位DT=30℃曲线：
- 在图（Vin vs I曲线）中找到DT=30℃的线。
确定交点（C点）：
- DT=30℃曲线与I=3.0 A的垂直线相交于点C。
读取Vin值：
- 从点C向y轴投影，得到输入电压Vin≈9.3 V。
关键点说明：
- 输入电压与电流呈非线性关系，温差越大，Vin越高。
- 该值用于计算制冷器的输入功率（Pin = Vin × I = 9.3 V × 3.0 A ≈ 27.9 W）。

2.3 制冷效率COP与输入电流I的关系

案例参数：

Th=50℃，Tc=20℃，目标电流I=3.0 A

127对温差电偶，6安培制冷器制冷效率COP、温差DT与输入电流I的函数关系

图3：127对TEC的COP vs I曲线（DT=30℃）。

步骤解析：

定位DT=30℃曲线：
- 在图（COP vs I曲线）中找到DT=30℃的线。
确定交点（D点）：
- DT=30℃曲线与I=3.0 A的垂直线相交于点D。
读取COP值：
- 此时制冷效率COP≈0.85，表示制冷量是输入功率的85%。
关键公式：
$\text{COP} = \frac{\text{制冷量 } Q_c}{\text{输入功率 } P_m} = \frac{Q_c}{V_{in} \times I}$
- 示例计算：COP = 25 W / (9.3 V × 3.0 A) ≈ 0.89（与图表读数误差可能因曲线精度而略有差异）。

4. 设计实例：激光二极管恒温器

一个激光二极管的恒温器中使用的热电制冷器为例，说明一个典型的设计过程。二极管和相关的电子器件被安装在一个双列直插式科瓦合金外壳内，并且，必须保持在25 ℃。将外壳安装在电路板上之后，通过测试得到其热阻值为6 ℃/W。激光电路损失热量为0.5W，并且整个体系的最高环境温度为35 ℃。
首先需要选择一个热电制冷器，其不但需要具有足够的制冷量来保持适当的温度，而且，还需要满足由于外壳所引起的尺寸上的要求。首先选择了一个18对热电偶臂1.2安培的热电制冷器，因为它具有适合的尺寸和所需的热电性能。

背景参数

需要维持的温度：25℃
外壳热阻：6℃/W
电子器件发热量：0.5 W
最高环境温度：35℃
选择制冷器型号：18对温差电偶，最大额定电流1.2 A

在这里插入图片描述

图5：18对TEC的Vin vs I曲线。

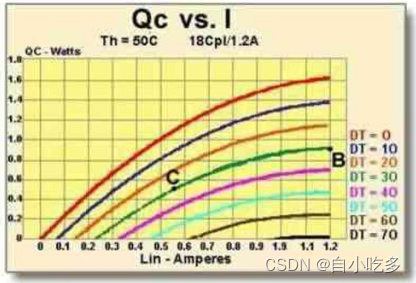
在这里插入图片描述

图6：18对TEC的Qc vs I曲线。

设计步骤

初始假设：
- 假设制冷器工作在最大电流（1.2 A）：
  - 输入电压Vin（图5）：1.2 A对应的Vin≈2.4 V（点A）。
  - 输入功率Pin = 1.2 A × 2.4 V = 2.9 W。
- 外壳最大热输入：
  - Pin（制冷器） + 电子器件发热量 = 2.9 W + 0.5 W = 3.4 W。
- 外壳温度升高：
  - 3.4 W × 6℃/W = 20.4℃。
- 热端温度Th：
  - 环境温度（35℃） + 温升（20.4℃） = 55.4℃。
首次计算制冷量（Qc）：
- 温差DT = Th - Tc = 55.4℃ - 25℃ = 30.4℃（近似30℃）。
- 在图1（Qc vs I曲线）中，DT=30℃的曲线：
  - 最大Qc≈0.9 W（点B）。
  - 目标Qc=0.5 W，沿DT=30℃曲线向下找到交点C，对应电流I≈0.55 A。
重新计算Th：
- 新输入电流I=0.55 A：
  - 输入电压Vin（图5）：0.55 A对应的Vin≈1.2 V（点D）。
  - 输入功率Pin = 0.55 A × 1.2 V = 0.66 W。
- 外壳热输入：
  - 0.66 W + 0.5 W = 1.16 W。
- 外壳温度升高：
  - 1.16 W × 6℃/W = 7℃。
- 新Th：35℃（环境） + 7℃ = 42℃。
- 新DT：42℃ - 25℃ = 17℃（需重新迭代）。
迭代计算：
- 第二次迭代：
  - DT=17℃，在图6中，DT=17℃的Qc曲线：
    - 目标Qc=0.5 W对应电流I≈0.45 A。
  - 计算Vin（图5）：0.45 A对应的Vin≈1.0 V。
  - Pin=0.45 A × 1.0 V = 0.45 W。
  - 外壳热输入：0.45 W + 0.5 W = 0.95 W。
  - Th=35℃ + (0.95 W × 6℃/W) = 35℃ + 5.7℃ = 40.7℃。
  - DT=40.7℃ - 25℃ = 15.7℃。
- 第三次迭代：
  - DT=15.7℃，对应Qc=0.5 W的电流I≈0.4 A。
  - 最终Th收敛至约39.8℃，DT≈14.8℃，误差<0.1℃。
结论：
- 18对温差电偶制冷器在电流≈0.4 A时可稳定维持25℃，满足需求。
- 实际应用中需考虑散热器设计，以降低Th并提高能效。

5. 注意事项与总结

散热器的重要性：
- 示例中假设散热器不存在，实际设计需通过散热器将Th降至更低，以提高制冷效率并减少输入功率。
- 例如，若使用散热器使Th=35℃（环境温度），则DT=10℃，Qc需求可进一步降低。
迭代计算的必要性：
- Th的计算需反复迭代，因Th与制冷器的输入功率直接相关，形成动态平衡。
- 忽略迭代可能导致Th估算偏差，影响制冷器选型。
参数选择关键点：
- 制冷量Qc：需覆盖设备发热量，同时留有冗余。
- 输入电压Vin：需匹配电源设计，避免过压损坏或欠压失效。
- COP最大化：优先选择COP峰值附近的工况（如案例中I=3.0 A时的COP≈0.85）。
图表使用技巧：
- Qc vs I曲线：用于确定工作电流和制冷能力。
- Vin vs I曲线：用于计算输入功率和电源需求。
- COP vs I曲线：用于优化能效，降低能耗。