【机器学习】梯度下降和牛顿法

最新推荐文章于 2023-06-29 11:27:48 发布

养老村村长

最新推荐文章于 2023-06-29 11:27:48 发布

阅读量333

点赞数 1

分类专栏：机器学习文章标签：机器学习

本文链接：https://blog.csdn.net/weixin_41456089/article/details/120743311

版权

机器学习专栏收录该内容

9 篇文章 1 订阅

订阅专栏

1. 先验知识

1.1 麦克劳林公式

1.1.1 公式

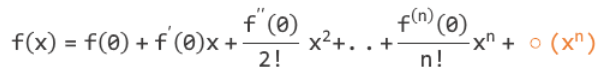
preview

1.1.2 作用

我们可以使用麦克劳林公式所构成的函数去近似拟合出在X=0附近任意一个函数。由于拟合出的是近似函数，所以麦克劳林公式的最后还要加上 $o(X^{n})$

1.1.3 案例

假设我们现在有一个关于函数 $e^{x}$ 的图像如下：

现在我们试图一阶麦克劳林公式去近似模拟这个函数在X=0附近的图像。

近似模拟 $e^{x}$ 的一阶麦克劳林公式：f(x) = 1 + x，图像如下：

如果放大观察x=0附近的两个函数的图像，会发现在x=0的极小范围内，麦克老林公式几乎完全近似 $e^{x}$ 的图像。这里，由于笔者画工稍差，放大后没有体现出来。

如果想要拟合的更好，我们可以考虑二阶麦克劳林公式去拟合

近似模拟 $e^{x}$ 的一阶麦克劳林公式： $f(x) = 1 + x + \frac{x^2}{2}$ ，图像如下：

1.1.4 小结

在分别查看一阶、二阶麦克劳林公式在X=0处对函数 $e^{x}$ 的拟合效果后，可以发现，越高阶的麦克劳林公式，拟合效果越好。可以想象，如果此时用n(n -> ∞)阶麦克劳林公式去拟合函数 $e^{x}$ ，会基本拟合出函数 $e^{x}$ 的图像。

1.2 泰勒公式

1.2.1 公式

1.2.2 作用

我们可以使用泰勒公式所构成的函数去近似拟合出在X=X0附近任意一个函数。由于拟合出的是近似函数，所以泰勒公式的最后还要加上 $o((X-X_0)^{n})$

1.2.3 与麦克劳林公式的区别

麦克劳林公式其实是泰勒公式的简化版，当泰勒公式中X0 = 0时，便是我们所说的麦克劳林公式。显然泰勒公式比麦克劳林公式更加强大，因为它可以让我们去近似拟合某一函数任意一点X0处的图像。

1.3 谈谈 $\Delta$ y与dy

如果函数f(x)在点( $x_0$ ， $f(x_0)$ )处是可微的，那么：

$\lim_{\Delta x \to 0} \frac{f(x_0+\Delta x) - f(x_0)}{\Delta x} ={f }'(x_0)$

当 $\Delta x \to 0$ 时，对式子进行简单变换，有：

$f(x_0+\Delta x) - f(x_0) =\Delta x{f }'(x_0)$

左侧 $f(x_0+\Delta x) - f(x_0)$ 即y的变化量 $\Delta y$ ，右侧 $\Delta x f'(x_0) = \Delta x \frac{dy}{dx} = dy$ 。

所以说，当 $\Delta x \to 0$ 时，我们可以用 $\Delta y$ 来近似 $dy$ ，即 $\Delta y = dy$ ，具体区别如下图所示：

1.4 线性近似的概念

由上述结论：当 $\Delta x \to 0$ 时，我们可以用 $\Delta y$ 来近似 $dy$ ，即 $\Delta y = dy$

假设切线方程为g(x), 此时切线方程g(x) = f(x) = e^x

所以，当 $x \to x_0$ 时，由公式 $f(x) - f(x_0) =(x-x_0){f }'(x_0)$ 可得：

$g(x) - f(x_0) =(x-x_0){f }'(x_0)$

因此，此时切线方程 $g(x)=f(x_0) + (x-x_0){f }'(x_0)$

这个g(x)也是我们所说的在x≈x0处对f(x)的线性近似结果

2. 梯度下降

2.1 公式

$x_{t} = x_{t-1} - \lambda f'(x_{t-1})$

2.2 思想

沿着下降最快的方向（负梯度）改变初始x，也就是初始x加上负梯度。

2.3 解释

2.3.1 从泰勒出发

通过1.4所述，f(x)在x=x0处的切线方程 $g(x)=f(x_0) + (x-x_0){f }'(x_0)$ ，这也是我们在1.2中所提到的泰勒公式。可知泰勒公式描述的就是函数f(x)在x0处的某一近似方程。如，一阶泰勒公式表示为f(x)在x=x0处的切线方程，二阶泰勒公式表示为f(x)在x=x0处的曲线方程（由于二阶导为方程增加了凹凸性的概念，所以此时可称呼为曲线方程）。

2.3.2 公式推导1

既然我们知道了g(x)为f(x)在x=x0处的切线方程，且 $g(x)=f(x_0) + (x-x_0){f }'(x_0)$

结合1.3中的图像，当x沿着左边切线的方向移动时，f(x) 是下降最快的，其中左边切线的方向也就是指负梯度。

令g(x)=0，即 $0 = f(x_0) + (x-x_0){f }'(x_0)$ ，得：

$x = x_0 - \frac{f(x_0)}{f '(x_0)}$

这就是我们所说的梯度下降，只不过此时的x从x0处移动到了令g(x)=0的x处，跨度较大，若该函数非凸函数，即有多个波峰波谷，很可能跨过当前最优解。

2.3.3 公式推导2

令f(x)为损失函数J(θ) ,对其进行一阶泰勒展开，

我们把 $\theta - \theta_0$ 转化为 $\lambda * d$ ,则 $J(\theta)\approx J(\theta_{0})+\lambda*d*J'(\theta_{0})$ （ $\lambda$ >0是单位向量d的长度，这里符号问题不大，就是倒来倒去的问题，d是单位向量）

这里 $\lambda$ 是常数，而后面两项都是向量，那么根据向量的规则，向量乘积转换为标量乘积和夹角余弦。

则可得：

这里theta是这两个向量的夹角。因为我们希望J(θ)越小越好，而 J(θ_0) 是随机初始化之后模型的输出，意味着这是一个常量，所以我们希望后面这一大陀的式子的取值越小越好，很明显cos(theta)=-1的时候最小了，而cos（theta）=-1表示这两个向量是方向相反的，所以可以得到 $d=\frac{-J'(\theta_{0})}{||J'(\theta_{0})||}$

结合上述 $\theta - \theta_0 = \lambda * d$ ，最终，

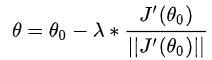
这样最得到了梯度下降法的参数的迭代公式了。

2.4 不同梯度下降说明和对比

2.4.1 随机梯度下降

随机梯度下降指每次随机取一个样本，根据该样本的位置找到负梯度，沿着负梯度下降。若该样本只有一维，则与我们上述推导出的公式一样。

2.4.2 小批量梯度下降

小批量梯度下降指每次随机采取部分样本，结合这些样本找到一个比较均衡的负梯度，再沿着负梯度下降。

2.4.3 批量梯度下降

批量梯度下降指每次采取全部样本，在全局上找到一个最优的负梯度，再沿着负梯度下降。

2.4.4 不同方法对比

随机梯度下降由于每次只随机采取一个样本，因此执行速度快，但由于样本采取较少，只能取到一个不太理想的局部最优解。

批量梯度下降由于每次都使用的全部样本，因此总能往全局最优的方向下降，但由于样本过多，执行速度慢。

小批量梯度下降分别改善了两者的缺点，在保证执行速度的同时，可以找到一个比较理想的局部最优解。

3 牛顿法

3.1 公式

3.2 思想

结合梯度下降，不仅沿着梯度下降最快的方向改变x，还考虑到了二阶导，也就是使用的二阶泰勒公式进行推导。换句话说，牛顿法除了考虑f(x)的变化率，还考虑到了f(x)的变化率的变化率。

3.3 公式推导

由于排版实在很累，笔者决定手写，如下图：

养老村村长

关注

1
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
【机器学习】梯度下降和牛顿法

1. 先验知识1.1 麦克劳林公式1.1.1 公式1.1.2 作用我们可以使用麦克劳林公式所构成的函数去近似拟合出在X=0附近任意一个函数。由于拟合出的是近似函数，所以麦克劳林公式的最后还要加上1.1.3 案例假设我们现在有一个关于函数的图像如下：现在我们试图一阶麦克劳林公式去近似模拟这个函数在X=0附近的图像。近似模拟的一阶麦克劳林公式：f(x) = 1 + x，图像如下：如果放大观察x=0附近的两个函数的图像，会发现在x=0的极小范围内，...
复制链接

扫一扫