1.计算梯度
对于函数
f ( x , y ) = x 2 s i n ( y ) f(x,y)=x^2sin(y) f(x,y)=x2sin(y)
如何计算这个函数的梯度
我们先计算函数的偏导
得到 ∂ f / ∂ x \partial f/\partial x ∂f/∂x 和 ∂ f / ∂ y \partial f/\partial y ∂f/∂y
梯度就是将这两个偏导打包成一个向量
用 ∇ f \nabla f ∇f表示（nabla）
所以，梯度捕捉了函数的所有偏导，那是不是函数的全导？
有多少个维度的输出，向量里面就有多少个偏微分的算子
2.梯度的几何意义
对于函数 f ( x , y ) = x 2 + y 2 f(x,y)=x^2+y^2 f(x,y)=x2+y2
函数的输入是二维
输出的梯度是一个一维的向量
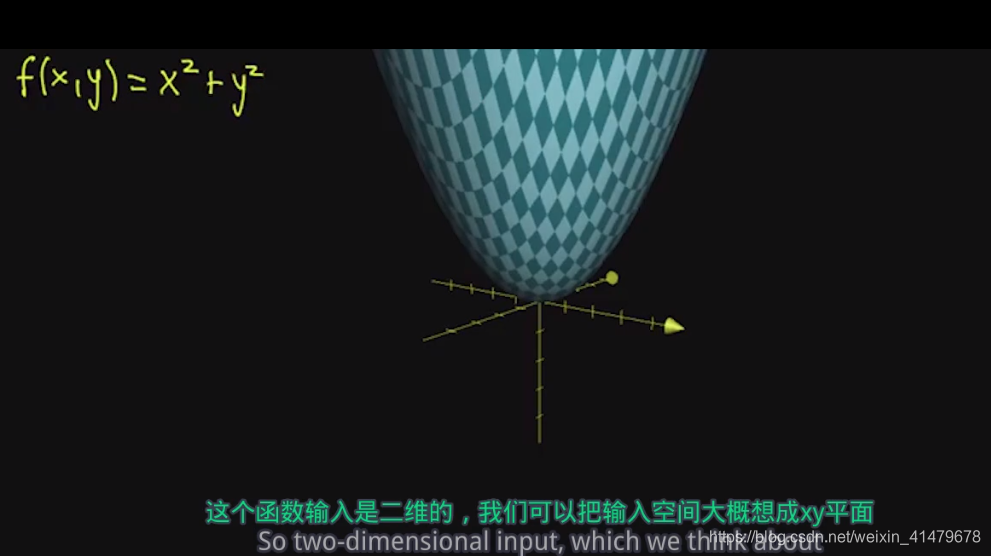
求出函数的梯度
求出的梯度向量（对于每一个点(x,y),输出的梯度向量是这个向量的两倍）
在函数的任何一点上，沿着梯度的方向，函数增长的最快
3.方向导数
理解了偏导就是函数输入空间上一个分量方向的变化，比如x轴上的变化，对函数输出的影响有多大
y方向的微调，对函数输出产生的影响
方向导数是说
有一个向量 ，假如我给定一个方向，比如 [ − 1 2 ] \begin{bmatrix} -1 \\ 2 \\ \end{bmatrix} [−12]
[ − 1 2 ] \begin{bmatrix} -1 \\ 2 \\ \end{bmatrix} [−12] 这个方向的微调，对函数的影响有多大
当然这个微调是极限值，这就是方向导数的定义
定义 [ − 1 2 ] \begin{bmatrix} -1 \\ 2 \\ \end{bmatrix} [−12]= v ⃗ \vec{v} v
往这个方向移动微小量，比如移动了h=0.001
方向导数函数
公理化的表示就是
有一个向量W，它的分量是[a,b],
向量w的任何一个方向f的方向导数表示为
∇ v ⃗ f = ∂ f ∂ x + ∂ f ∂ y \nabla_{\vec{v}}f=\frac{\partial f}{\partial x} \quad+\frac{\partial f}{\partial y} \quad ∇vf=∂x∂f+∂y∂f
这其实也是向量的点积
向量 [ a b ] \begin{bmatrix} a \\ b \\ \end{bmatrix} [ab]
与向量f的梯度 [ ∂ f ∂ x ∂ f ∂ y ] \begin{bmatrix} \frac{\partial f}{\partial x} \quad \\ \frac{\partial f}{\partial y} \quad \\ \end{bmatrix} [∂x∂f∂y∂f]
的点积
4.梯度，方向导数与斜率
函数 f ( x , y ) = x 2 y f(x,y)=x^2y f(x,y)=x2y
我们取输入空间内的向量 v ⃗ = \vec{v}= v= [ 1 1 ] \begin{bmatrix} 1 \\ 1 \\ \end{bmatrix} [11]
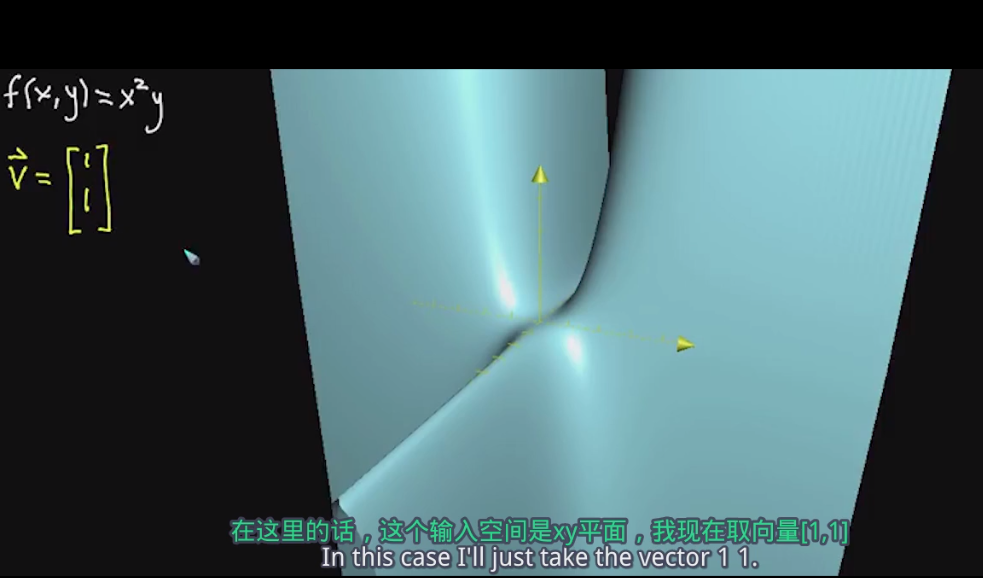
我们来讨论函数f在v方向的方向向量
沿着向量v的方向切割函数图像
这样向量v就落在了这个切割平面上
取[-1,-1]评估方向向量
类似的，我们取切割交线上的一点求与这一点的斜率是一样
为了方便后面考虑，把向量v定义成单位长度的向量，让向量v的长度等于1
2
\sqrt{2}
2/2
=1.414/2
=0.7
sin45=0.7= 2 \sqrt{2} 2/2/1
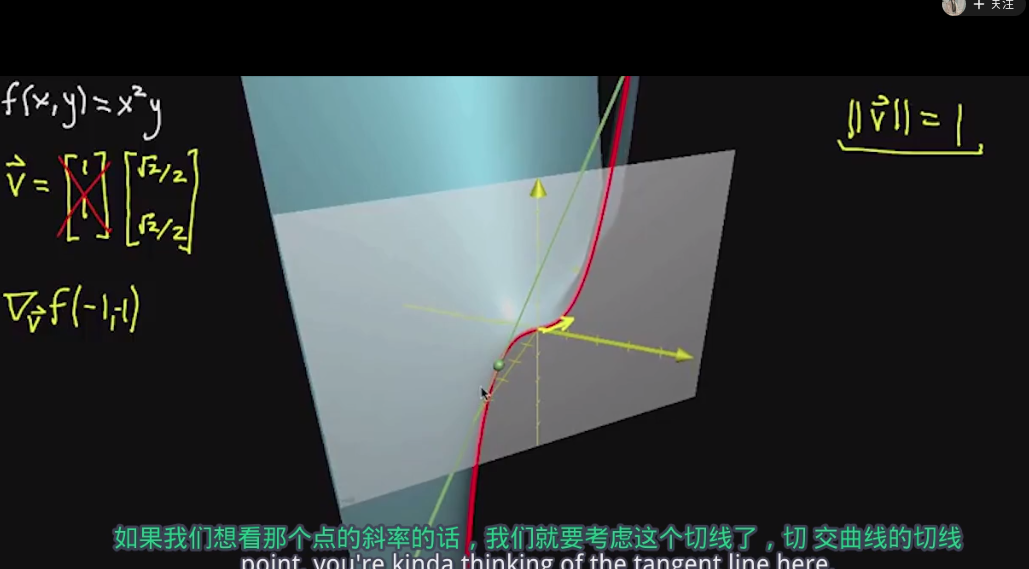
这个点的切线就等于函数的斜率，也是向量v方向导数
∂
f
/
∂
v
⃗
\partial f/\partial\vec{v}
∂f/∂v就表示在v方向的微调，引起函数的变化
当我们计算方向导数时候
计算的是f的 梯度向量 与 方向向量 的 点积
f的梯度向量等于：
我们求的是点[-1,-1]的梯度，带入得到：
计算得到
2
+
2
/
2
\sqrt{2}+\sqrt{2}/2
2+2/2
(点积计算：
2
∗
2
/
2
+
1
∗
2
/
2
2*\sqrt{2}/2+1*\sqrt{2}/2
2∗2/2+1∗2/2)
2万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
