隧道断面超欠挖概念
隧道断面超欠挖是指在隧道施工过程中,实际开挖断面与设计开挖断面之间的偏差。
- 定义
超挖:实际开挖断面大于设计开挖断面。
欠挖:实际开挖断面小于设计开挖断面


- 影响及控制意义
影响:
超挖会增加工程成本,可能导致围岩失稳,影响隧道结构的稳定性。
欠挖会降低隧道净空,影响后续衬砌施工和运营安全。
控制意义:
严格控制超欠挖可以保证隧道施工质量,减少安全隐患,提高工程经济效益。
施工规范和标准
隧道超欠挖的控制依据主要来源于相关施工规范和技术标准



条文摘要:
第11.2.6条规定:
隧道开挖断面允许超欠挖限值应符合设计要求,未作规定时应满足:
- 拱部超挖不得超过设计断面外轮廓100 mm;
- 侧壁不得超过150 mm;
- 欠挖不得影响结构施工和净空要求。

条文摘要(第9.3节):
超挖控制限值(单位:mm): - 拱部 ≤ 100 mm
- 侧墙 ≤ 150 mm
- 仰拱 ≤ 100 mm
- 欠挖应满足净空和衬砌施工要求。
- 且强调“不得影响支护结构的安全性与施工工艺”。
(上述标准,于2025年5月18日查询,属于现行规范。)
《公路隧道施工技术规范》(JTG F60-2009,已废止,新规范为JTG/T3660-2020)中对超欠挖规定:应严格控制欠挖。拱脚和墙脚以上1m内范围严禁欠挖。应尽量减少超挖,不同围岩地质条件下的允许超挖值规定如下表(F69-2009版,目前没找到最新标准的文件,找到后进行更新):


超欠挖计算方法
常用体积计算方法
- 断面法(最常用):
原理:在两个相邻断面间,用平均面积乘以断面间距
公式: V = Σ [ ( A 1 + A 2 ) / 2 × L ] V = Σ[(A₁ + A₂)/2 × L] V=Σ[(A1+A2)/2×L]
A 1 A_1 A1, A 2 A_2 A2: 相邻断面的超欠挖面积; L L L:断面间距
优点:计算简单,适用于规则间距断面
缺点:精度受断面密度影响
- 三角网法:
原理:构建设计面和实际开挖面的三角网,计算两曲面间体积
优点:精度高
缺点:计算复杂,需要处理大量三角面片
- 格网法:
原理:将区域划分为格网,计算每个格网柱体的体积差
优点:适合规则区域
缺点:精度受格网大小影响
- 点云直接计算法:
原理:计算每个点到设计面的距离,积分得到体积
优点:直接利用原始数据
缺点:计算量大
def calculate_overbreak_underbreak(scan_pcd, section_pcd, route_pcd, section_frames, output_dir="output/OUbreak_pic"):
"""
优化后的超欠挖计算函数,解决点云包围和空点云问题
"""
import os
import matplotlib.pyplot as plt
from shapely.geometry import Polygon, MultiPolygon
from shapely.ops import clip_by_rect, unary_union
from scipy.spatial import Delaunay
os.makedirs(output_dir, exist_ok=True)
route_points = np.asarray(route_pcd.points)
section_points = np.asarray(section_pcd.points)
scan_points = np.asarray(scan_pcd.points)
total_sections = len(route_points)
points_per_section = len(section_points) // total_sections
section_areas = []
for i in range(total_sections):
try:
frame = section_frames[i]
start_idx = i * points_per_section
end_idx = (i + 1) * points_per_section
design_points = section_points[start_idx:end_idx]
# 投影扫描点到断面,并增加水平过滤
distances = np.dot(scan_points - frame['point_base'], frame['dir_vec'])
mask = np.abs(distances) < 0.2 # 20cm阈值
nearby_points = scan_points[mask]
# 检查是否有扫描点
if len(nearby_points) == 0:
print(f"警告: 断面 {i} (里程 {route_points[i,0]:.3f}m) 无点云数据,跳过计算")
section_areas.append((0.0, 0.0))
continue
# 转换到2D局部坐标系
local_design = []
for point in design_points:
vec = point - frame['point_base']
x = np.dot(vec, frame['x_axis'])
y = np.dot(vec, frame['y_axis'])
local_design.append([x, y])
local_scan = []
for point in nearby_points:
vec = point - frame['point_base']
x = np.dot(vec, frame['x_axis'])
y = np.dot(vec, frame['y_axis'])
local_scan.append([x, y])
# 创建多边形
design_poly = Polygon(local_design).convex_hull
scan_poly = Polygon(local_scan).convex_hull if len(local_scan) >= 3 else Polygon()
# 计算有效扫描区域(避免完全包围误判)
if not scan_poly.is_empty:
# 计算扫描点与设计面的交集
if design_poly.within(scan_poly):
# 实测轮廓点完全包围设计断面,无欠挖
overbreak = scan_poly.difference(design_poly)
underbreak = Polygon()
valid_scan = design_poly
else:
valid_scan = scan_poly.intersection(design_poly)
overbreak = scan_poly.difference(design_poly)
underbreak = design_poly.difference(valid_scan) if not valid_scan.is_empty else design_poly
else:
overbreak = Polygon()
underbreak = design_poly
valid_scan = Polygon()
# 计算面积
def get_area(geom):
if geom.is_empty:
return 0.0
if isinstance(geom, (Polygon, MultiPolygon)):
return geom.area
return 0.0
overbreak_area = get_area(overbreak)
underbreak_area = get_area(underbreak)
section_areas.append((overbreak_area, underbreak_area))
# 可视化===不同绘图顺序会得到不同可视结果
plt.figure(figsize=(10, 8))
# 先绘制超挖区域
if not overbreak.is_empty:
if isinstance(overbreak, Polygon):
plt.fill(*overbreak.exterior.xy, 'r', alpha=0.3, label='Overbreak')
elif isinstance(overbreak, MultiPolygon):
for poly in overbreak.geoms:
plt.fill(*poly.exterior.xy, 'r', alpha=0.3)
# 绘制扫描点云的有效轮廓
if not scan_poly.is_empty and hasattr(scan_poly, 'exterior'):
plt.plot(*scan_poly.exterior.xy, 'b--', label='Scan Area')
if hasattr(valid_scan, 'exterior'):
plt.plot(*valid_scan.exterior.xy, 'b-', label='Valid Scan')
# # 绘制有效扫描区域
# if not valid_scan.is_empty and hasattr(valid_scan, 'exterior'):
# plt.plot(*valid_scan.exterior.xy, 'b-', label='Valid Scan')
# 绘制设计轮廓(最上层)
if hasattr(design_poly, 'exterior'):
plt.fill(*design_poly.exterior.xy, facecolor='white', edgecolor='none', zorder=1)
plt.plot(*design_poly.exterior.xy, 'g-', label='Design Profile')
# 绘制欠挖区域
if not underbreak.is_empty:
if isinstance(underbreak, Polygon):
plt.fill(*underbreak.exterior.xy, 'y', alpha=0.3, label='Underbreak')
elif isinstance(underbreak, MultiPolygon):
for poly in underbreak.geoms:
plt.fill(*poly.exterior.xy, 'y', alpha=0.3)
plt.title(f"Section at Mileage {route_points[i,0]:.2f}m\n"
f"Overbreak: {overbreak_area:.4f} m² | Underbreak: {underbreak_area:.4f} m²")
plt.legend()
plt.grid(True)
plt.axis('equal')
plt.savefig(os.path.join(output_dir, f"section_{i:04d}.png"))
plt.close()
except Exception as e:
print(f"处理断面 {i} 时出错: {str(e)}")
section_areas.append((0.0, 0.0))
return np.array(section_areas)
以断面法进行编程实现
计算超欠挖面积
- 输入数据
隧道点云
设计断面
线路中心线,用于区分每一个断面的位置
每个断面对应的局部坐标系 - 每一断面的处理流程
对于每个断面i:
a. 提取该断面的设计断面点
design_points = section_points[start_idx:end_idx]
b. 找到靠近断面平面(20cm以内)的扫描点
distances = np.dot(scan_points - frame['point_base'], frame['dir_vec'])
mask = np.abs(distances) < 0.2
nearby_points = scan_points[mask]
c. 将三维点转换为局部二维平面坐标系(断面坐标系)
对每个点进行投影:
x
=
(
P
−
P
0
)
⋅
X
a
x
i
s
y
=
(
P
−
P
0
)
⋅
Y
a
x
i
s
x = (P - P_0) \cdot X_{axis} \\ y = (P - P_0) \cdot Y_{axis}
x=(P−P0)⋅Xaxisy=(P−P0)⋅Yaxis
其中,
P
P
P是点,
P
0
P_0
P0是断面参考点,
X
a
x
i
s
X_{axis}
Xaxis、
Y
a
x
i
s
Y_{axis}
Yaxis是局部平面X、Y周单位向量。
d. 构建2D多边形
- design_poly: 由设计断面点形成的设计多边形
- scan_poly:由扫描点形成的扫描轮廓多边形
e. 计算超欠挖区域(用到了多边形差集、交集操作,来自Shapely库)
- 如果scan_poly完全包围design_poly:说明无欠挖,只有超挖
overbreak = scan_poly.difference(design_poly)
underbreak = Polygon()
- 否则:计算
-
- 有效扫描区域(交集):valid_scan = scan_poly ∩ design_poly
-
- 超挖:scan_poly - design_poly
-
- 欠挖:design_poly - valid_scan
f. 计算面积
对多边形或复合多边形:
A
=
A
r
e
a
(
P
o
l
y
g
o
n
)
A = Area(Polygon)
A=Area(Polygon)
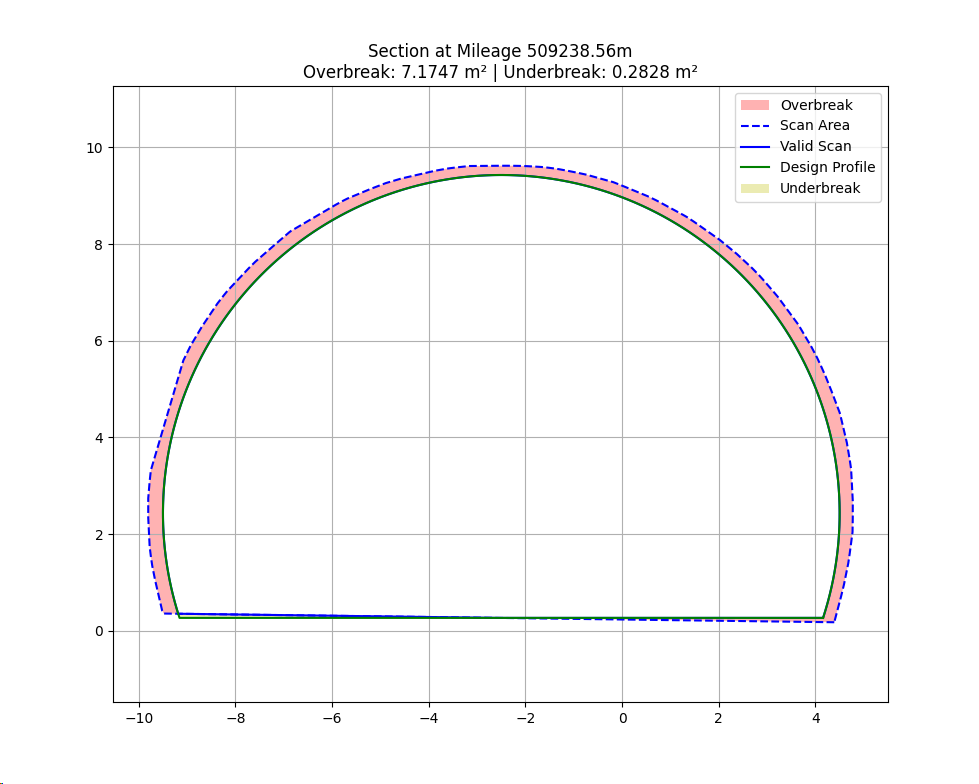
g. 绘图并保存结果
- 图像中标注:
-
- 超挖区域
-
- 欠挖区域
-
- 扫描轮廓
-
- 设计轮廓
- 在图中写明面积信息
计算超欠挖体积
- 输入数据
section_areas: n × 2的数组 # 每一行表示一个断面的(超挖面积,欠挖面积)
mileage: n 长度的数组 # 每个断面的中心里程
- 计算逻辑
在每两个相邻断面之间 i i i与 i + 1 i+1 i+1,用平均面积法估算体积:
原理:
对区段长度 L i = m i l e a g e i + 1 − m i l e a g e i L_i = mileage_{i+1}- mileage_{i} Li=mileagei+1−mileagei,其估算体积为:
V i = A i + A i + 1 2 ⋅ L i V_i = \frac{A_i + A_{i+1}}{2} \cdot L_i Vi=2Ai+Ai+1⋅Li
avg_overbreak = (A_i_over + A_next_over)/2
avg_underbreak = (A_i_under + A_next_under)/2
def calculate_volume(section_areas, mileage):
"""
基于断面面积计算超欠挖体积
:param section_areas: 每个断面的超欠挖面积数组 (n_sections x 2)
:param mileage: 路线里程数组
:return: (total_overbreak_vol, total_underbreak_vol)
"""
total_overbreak = 0.0
total_underbreak = 0.0
for i in range(len(section_areas) - 1):
L = mileage[i+1] - mileage[i] # 断面间距
# 平均面积法
avg_overbreak = (section_areas[i,0] + section_areas[i+1,0]) / 2
avg_underbreak = (section_areas[i,1] + section_areas[i+1,1]) / 2
total_overbreak += avg_overbreak * L
total_underbreak += avg_underbreak * L
return total_overbreak, total_underbreak
结果可视化




























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








