期望值为无穷大的博彩游戏，真的花多少钱玩都值得吗？

最新推荐文章于 2025-05-05 15:52:33 发布

多彩电脑

最新推荐文章于 2025-05-05 15:52:33 发布

阅读量1.1k

点赞数 18

分类专栏：有意思的数学知识文章标签：游戏概率论数学建模

本文链接：https://blog.csdn.net/weixin_41640959/article/details/142901406

版权

有意思的数学知识专栏收录该内容

6 篇文章

订阅专栏

我们知道，一般当人们在投资方面进行决策的时候，往往会根据所期望的收益，决定花多少钱投入。但是，当人们玩博彩游戏时，似乎不再遵循这个原则。文[1]指出，通常博彩游戏的期望值都是庄家赚钱，玩家亏钱，只有这样庄家才能盈利。换句话说，玩家如不玩博彩游戏，期望收益是0，而如果玩博彩游戏，期望收益是负数[1]。但是即便如此，仍然有很多人玩博彩游戏，因为期望收益并不是人们做决策的唯一考虑因素。

但如果博彩游戏的期望值真的有利于玩家了，也就是说玩的价格如果小于期望收益，玩家就会愿意玩吗？其实不一定。本文介绍两种博彩游戏，其玩家的期望收益达到无穷，也就是说无论庄家如何定价，只要是有限大，玩家的期望收益都是正数，但玩家未必愿意玩。本文分析不愿意玩的原因。

一、期望值为无穷大的博彩游戏简介

（一）圣彼得堡游戏

1738年，数学家丹尼尔伯努利（Daniel Bernouli）的堂兄弟尼古拉伯努利提出了一个圣彼得堡游戏[2]。游戏规则：抛掷硬币，并令正面或反面作为成功的定义。如果第一次抛掷成功，得奖金2元；第二次才成功，4元；第 $n$ 次成功， $2^n$ 元[2]。那么收益值 $R$ 的期望值

$E(R) = {1\over 2}2^{1}+{1\over 2^2}2^{2}+...+{1\over 2^n}2^{n}+...={1}+{1}+...=+\infty$

（二）翻镜子游戏

现在，将两面镜子放在地面上，然后随机转动一面镜子，停下后两面镜子之间会呈一个角度。这两面镜子之间的角度用如下方式定义：

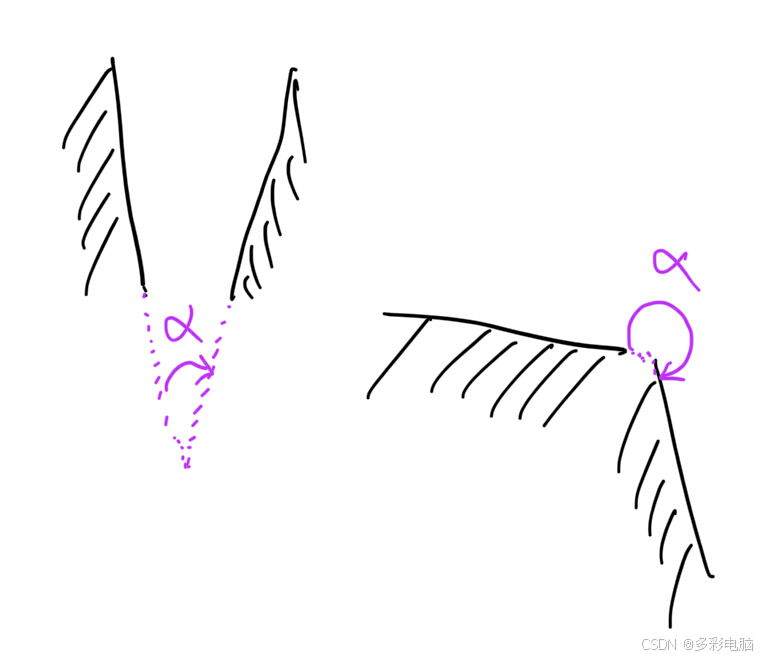
然后将物体放在镜子前，该物体在镜子中能成几个像，就得奖金几元。文章[3]中指出，一个物体在两个互成角度 $\alpha$ （角度值）的平面镜中成的像的个数 $N$ 是：

$N={360\over \alpha}-1$

这里 $\alpha$ 在 $[0,360]$ 之间均匀分布。显然，如果两面镜子恰好平行，镜子面前的物体在镜子中会成无穷多个像。成像个数 $N$ 的期望值这样求：

首先，要求出 $N$ 的概率分布。先从求 $\alpha$ 的累积分布函数（Cumulative Distribution Function）开始。

$CDF(\alpha)={\alpha\over 360}$

由于 $N$ 和 $\alpha$ 之间的函数在 $\alpha\in [0,360]$ 单调递减

$P(N\leq {360\over \alpha}-1)=1-{\alpha\over 360}=1-{1\over N+1}$ （1）

通过导数运算计算 $N$ 的概率密度函数（probability density function）

$pdf(N)={dP(N)\over dN}={1\over (N+1)^2}$

现在计算期望值

$E(N)=\int_0^{+\infty}N{1\over (N+1)^2}dN=\int^{+\infty}_0(N+1){1\over (N+1)^2}dN-\int^{+\infty}_0{1\over (N+1)^2}dN$

$=\int_1^{+\infty}{1\over N}dN-\int_1^{+\infty}{1\over N^2}dN=+\infty$

以上两个游戏的期望值均为无穷，也就是说如果从期望收益而言，玩家花多少钱都是愿意的。

二、游戏运行效果模拟

现在，用Matlab模拟这两个游戏。把这两个游戏玩10000次，计算每次得到奖金的平均值。同样的操作进行10次，观察结果。

圣彼得堡游戏：

function num_of_tosses = StPetersburgGame()
    tossed = 0;
    while true
        result = unidrnd(2,1); %randomly pick between 1 and 2 
        tossed = tossed + 1;
        if result == 2 %If 2 then quit
            break
        end
    end
    num_of_tosses = tossed;
end

function reward = playStPersburg()
    num_of_tosses = StPetersburgGame();
    reward = 2 ^ (num_of_tosses);
end

avgResults = zeros(10,1);
for jj = 1:10
    rewards = zeros(10000,1);
    for ii = 1:10000
        rewards(ii) = playStPersburg();
    end
    avgResults(jj) = mean(rewards);
end
avgResults

10次的平均值分别为

8.5502

12.0251

6.4399

10.8072

5.1178

7.5799

7.3281

7.1395

5.6659

7.3176

从中可以看出，奖金的平均值并不收敛，可以说明其期望值不能稳定存在。但是，也似乎并没有出现很大的数值。

同样，翻镜子游戏：

function num_of_objects = mirrorGame()
    a = rand() * 360;
    num_of_objects = 360 / a - 1;
end

avgResults = zeros(10,1);
for jj = 1:10
    rewards = zeros(1000000,1);
    for ii = 1:1000000
        rewards(ii) = mirrorGame();
    end
    avgResults(jj) = mean(rewards);
end
avgResults

10次的平均值分别为

23.2536

48.4419

23.6588

12.1210

12.3441

25.6226

13.1225

12.1266

12.9606

15.4802

三、分析

从上述实验结果可看出，通过模拟，并不会产生很大的平均值，似乎没有体现出“趋向无穷大”的现象。如果玩家看到了这样的结果，不会愿意花很多钱玩这个游戏。然而，为什么在现实中，会“辜负”期望呢？

关于这一点，需要从这些非常大的值出现的概率入手。

（一）大值概率

以圣彼得堡游戏为例，再次回忆出现各奖金值的概率

概率	奖金
$1\over 2$	$2$
$1\over 2^2$	$2^2$
$1\over 2^3$	$2^3$
...	...
$1\over 2^{n}$	$2^{n}$
...	...

也就是说，虽然得期望得到的奖金是无穷大，但得到奖金超过 $2^{n}$ 的概率，小于 ${1\over 2^{n+1}}+{1\over 2^{n+2}}+...={{1\over 2^{n+1}}\over 1-{1\over 2}}={1\over 2^n}$

例如，奖金超过 $16$ 的概率小于 $1\over 16$ 。对于发生的概率为 $p$ 的事件，两次发生之间未发生该事件的实验次数（即间隔次数）期望值为 $1-p\over p$ [4]。因此，对于此情况，期望现象是在一次出现奖金超过 $16$ 之后，玩 $15$ 次游戏都未出现奖金超过 $15$ 的情况，直到第 $16$ 次才再次出现。

对于翻镜子游戏也是如此。如式（1）所示， $P(N>x)=1-(1-{1\over x+1})={1\over x+1}$ 。

简单地说，就是得到大奖金的情况，期望是在玩了很多次后，才会出现。

还是以圣彼得堡游戏为例，由于得到奖金超过 $x$ 的概率小于 $1\over x$ ，我们期望前 $x-1$ 次都未能得到超过 $x$ 的奖金（指单次），到第 $x$ 才得到。而之前 $x-1$ 次玩这个游戏得到的总奖金的期望值为

$R(x)=(x-1)({{1}+2^2({1\over 2})^2+...+2^{c}({1\over 2})^c\over 1-{({1\over 2})^{c+1}\over 1-{1\over 2}}})$

其中 $c=\log_2x-1$

$R(x)=(x-1)({{1}+2^2{1\over 2^2}+...+2^{c}{1\over 2^{c}}\over 1-{{1\over x}\over 1-{1\over 2}}})={\log_2x-1\over 1-{2\over x}}$

所以，期望在玩了 $x$ 次后，得到的总奖金才会超过 $R_{expect}(x)=(x-1){\log_2x-1\over 1-{2\over x}}+x$

特别的，当 $x=2$ 时，期望情况是第一次得奖金为 $2$ ，第二次得到的奖金超过 $4$ ，所以第二次玩后总奖金才会超过 $6$ ，即 $R_{expect}(2)=6$

将 $R_{expect}(x)$ 函数用Matlab实现

function reward = tryXTimesEst(x)
    if x > 2
        reward = x + (x-1) * ((log(x) / log(2) - 1)) / (1 - 2/x);
    else
        reward = 6;
    end
end

以之前的 $x=2^4=16$ 为例， $R_{expect}(16)=67.4286$ ，也就是说在玩了 $16$ 次后，总奖金期望才会高于 $67.4286$ 。

（二）游戏模拟

现在用Matlab模拟该游戏，玩 $16$ 次，计算总奖金。该动作做 $10$ 次

function overallReward = tryXTimes(x) %该代码模拟玩游戏x次，计算总奖金
    overallReward = 0;
    for ii = 1:x
        overallReward = overallReward + playStPersburg();
    end
end

for ii = 1:10
    tryXTimes(16)
end
tryXTimesEst(16)

10次的运行结果，即总奖金，如下

128

136

376

186

180

从表中可看出，10次里有9次总奖金超过了 $R_{expect}(16)$ ，其中有一次非常高。

（三）进一步实验

现在尝试令 $x=2,4,8,16,32$ ，计算 $R_{expect}(x)$ ，同时对每一个玩 $x$ 次的情况，运行 $50$ 次，统计有多少次总奖金超过了 $R_{expect}(x)$ 。

注，运行的次数也可以自行调整，改numberOfTimes的变量值。

xs = [2, 4, 8, 16, 32];
numberOfTimes = 50;
rewEst = zeros(5,1);
rewReal = zeros(5, numberOfTimes);
for xIdx = 1:length(xs)
    rewEst(xIdx) = tryXTimesEst(xs(xIdx));
    for ii = 1:numberOfTimes
        rewReal(xIdx, ii) = tryXTimes(xs(xIdx));
    end
end
rewEst
compTable = (rewReal > rewEst);
compTimes = sum(compTable, 2);
compTimes/numberOfTimes