机器学习05-聚类算法（python）

橙子小哥的代码世界

已于 2024-09-14 21:20:41 修改

阅读量1.2k

点赞数 19

文章标签：机器学习算法聚类

于 2024-09-14 15:17:37 首次发布

本文链接：https://blog.csdn.net/weixin_41645791/article/details/142259407

版权

第一：聚类算法的概念

大家好，今天我们来学习聚类算法。什么是聚类算法呢？其实你可以把它想象成一种“分组”的过程。我们根据事物之间的相似性，把相似的东西放在一组里，而把不同的东西分到不同的组中。举个例子，你走进一个动物园，看到很多动物。如果我们根据它们的生活方式（例如，水里游泳的动物、陆地上行走的动物）把它们分成几组，这就是一种简单的聚类思想。

聚类的目的就是在没有预先“告诉”计算机类别的情况下，让计算机自己通过数据的特征来发现内在的结构和模式。这种方法叫做无监督学习，因为我们并没有提供“正确答案”，而是让计算机自己寻找答案。

实际例子：

假设你有一大堆水果，你想把它们分类。你可以根据水果的颜色（红色、绿色、黄色）或者形状（圆形、椭圆形、长条形）把它们分组。如果根据颜色来分，红苹果和草莓会在同一组，但如果根据形状来分，苹果和橘子可能会被分在一起。

这就类似于在不同的聚类算法下，可能得到不同的分组结果。

第二：聚类算法的应用

聚类算法在我们日常生活中有很多应用。大家知道，很多网站会根据你的浏览记录、购物习惯为你推荐商品，这背后就用到了聚类算法。比如，亚马逊会根据其他和你有相似购买行为的用户给你推荐你可能喜欢的商品。

不仅如此，新闻网站也会根据内容的相似度把新闻自动归类，方便你找到感兴趣的内容。再比如，在交通管理中，聚类算法可以用于识别恶意流量，帮助我们防范网络攻击。

实际例子：

想象一下，当你打开购物网站，想买一件衣服时，网站自动推荐了很多你可能感兴趣的其他衣服。这是因为网站通过聚类算法分析了成千上万的用户购买行为，找到了和你相似的用户，并推荐给你他们喜欢的商品。这个过程就是聚类算法在背后工作的结果。

第三：聚类算法分类

聚类算法有很多种类，今天我们来了解两种分类方式。

第一种是按照聚类的“颗粒度”来分类。可以把它理解为粗分类和细分类。比如，你可以先大致地把动物分成哺乳动物和非哺乳动物，这是粗分类；然后再把哺乳动物分成狗、猫、狮子，这就是细分类。

第二种是按聚类的具体实现方式来分类。常见的几种方式有：

• K-Means：它根据某些中心点，把数据点分到最接近的组中。

• 层次聚类：它像树一样，逐步把数据细分，直到每个类别都很具体。

• DBSCAN：它基于数据点的密度来聚类，非常适合处理形状复杂的数据。

实际例子：

大家可以把这想象成我们把朋友分类。粗分类的话，我们可以把朋友分成“玩得来的”和“不太玩得来的”；细分类的话，我们可以把“玩得来的朋友”再分成“喜欢运动的朋友”和“喜欢艺术的朋友”。不同的聚类算法就像我们用不同的方式去给朋友分类。

第四：聚类算法总结

聚类算法的核心是把相似的事物分在一起，常用的衡量标准是欧式距离，即两点之间的直线距离。它是一种无监督学习算法，因为我们事先并不知道数据的正确分组，计算机会根据数据之间的相似性自动形成分类。

我们今天还学习了聚类算法的几种分类方法，包括按“颗粒度”分类和按具体实现方法分类。常见的聚类算法有 K-Means、层次聚类和基于密度的 DBSCAN 等。

实际例子：

聚类算法就像我们分组活动时的做法，比如体育课上我们可以根据身高把同学分成几组，或者根据跑步速度来分组。不同的分组方法就对应着不同的聚类算法。

第五：聚类算法练习

最后，我们来做一个简单的小练习。问题是：在聚类算法中，样本之间的相似度是否只能通过欧式距离来衡量？答案是不一定，欧式距离只是其中一种方法，其他的衡量方式还有曼哈顿距离、余弦相似度等。

我们今天学习的是聚类算法。聚类算法是什么呢？简单来说，它是一种无监督学习方法，主要用于根据样本的相似性将数据分组。没有事先给出类别标签，算法会通过计算样本之间的相似度，把相似的样本自动归到一个组里，不同的算法和距离衡量方法会产生不同的分组结果。

相似度衡量：

在聚类过程中，如何判断两个样本是否相似呢？通常，我们使用欧式距离来衡量，也就是两点之间的直线距离。就像你站在两棵树之间，量它们之间的直线距离，这就是欧式距离。

但欧式距离并不是唯一的衡量方式，其他常见的方法还有：

• 曼哈顿距离：就像在城市街道上走路，你只能沿着街道拐弯，而不能穿越建筑物，这种方式就是曼哈顿距离。

• 余弦相似度：用来衡量两个向量的方向。即使两个人的生活方式不同，如果他们兴趣爱好相同，余弦相似度也会很高。这种方法通常用于文本分析。

K-Means算法简介：

聚类算法中，K-Means 是一种常用的聚类方法。它的过程大概是这样：

1. 选择K：你首先选择你想分成几组，比如 3 组。

2. 初始化质心：算法随机选择 3 个点作为每组的中心（质心）。

3. 分配数据点：接着，算法根据每个数据点到质心的距离，把它分配到离自己最近的组里。

4. 更新质心：每个组的中心会重新计算，质心会移动。

5. 重复分配：不断重复以上过程，直到质心不再变化或达到设定的迭代次数。

实际例子：

想象你有 50 名学生，他们的数学和英语成绩不同。你想把他们分成 3 组。首先随机选择 3 名学生的成绩作为质心，然后算法根据每个学生的成绩将他们分配到最近的质心组，最后通过迭代更新每组的中心点，直到不再变化。这就是 K-Means 的工作原理。

常见的聚类算法分类：

1. 颗粒度分类：粗聚类和细聚类。

2. 实现方法：K-Means、层次聚类、DBSCAN 等。

应用场景：

聚类算法在现实生活中有很多应用，比如：

• 商品推荐：根据用户的购物行为分组，推荐你可能喜欢的商品。

• 新闻分类：根据新闻内容相似度自动将新闻分组。

• 网络流量分析：用于识别异常网络流量和恶意行为。

总结：

今天我们学习了聚类算法的基本概念、常见算法以及如何通过不同的距离衡量方法来判断样本的相似性。我们还了解了 K-Means 算法的工作原理，以及它在现实生活中的应用场景。

希望大家能够对聚类算法有一个基本的了解。下次我将深入探讨具体算法的细节，看看它们是如何在实际问题中运作的。

我们会一步步走，通过实例和代码来理解这些内容，让大家能够自己动手实现聚类算法。让大家不仅能理解聚类的基本概念，还能够掌握如何使用Python库实现聚类分析。

第七：聚类算法API

在 Python 中，我们可以很方便地使用 sklearn.cluster.KMeans 来实现 K-Means 算法。这是一个常用的机器学习库，里面有许多封装好的算法，包括 K-Means。

在使用 K-Means 时，我们需要设置一个参数叫 n_clusters，这个参数告诉算法我们想把数据分成几组。比如，如果 n_clusters=4，表示我们想把数据分成4个簇。

• fit(x)：计算并拟合数据，找到质心。

• predict(x)：根据训练好的模型预测每个数据点属于哪个簇。

• fit_predict(x)：这一步骤同时完成拟合和预测，直接告诉我们每个样本属于哪个簇。

实际例子：

想象一下，你有一堆学生的成绩单，想按照他们的成绩把他们分成几组优良中差。你设置 n_clusters=3，那么算法会自动把这些学生分成3组，每组的学生成绩最接近组内其他人的成绩。

第八：使用 K-Means 模型探索聚类

这里我们通过代码实例展示如何使用 K-Means 进行数据的聚类分析。我们生成一些二维数据，然后使用 K-Means 算法将这些数据分成不同的簇，并将结果可视化。

你可以看到四个不同的散点图，这些图显示了随着簇的数量变化，数据被如何分成不同的组。每个颜色代表一个簇，不同簇的点聚集在一起。

实际例子：

比如你有1000个顾客的数据，每个顾客有两个特征：年龄和年收入。通过 K-Means 算法，我们可以把这些顾客分成不同的消费群体，比如高收入群体、低收入年轻群体等。

第9：代码解析

接下来我们逐步讲解如何实现聚类分析：

1. 导入工具包：我们使用 KMeans 来进行聚类，用 matplotlib 来画图，用 make_blobs 生成模拟数据。

2. 创建数据集：我们使用 make_blobs 生成1000个样本，每个样本有2个特征，形成4个不同的中心点。

3. 聚类分析：我们调用 KMeans 进行聚类，并使用 fit_predict 方法得到每个样本的簇分类结果。

4. 评估模型：我们使用 calinski_harabasz_score 来评估模型的聚类效果。数值越大，说明模型的效果越好。

实际例子：

就像我们把水果分组，我们可以根据它们的颜色和形状来分，如果分得越精准，组内的水果会更加相似，组间差异越大。

第10页：总结

1. 我们使用了 KMeans 进行聚类分析，主要参数是 n_clusters，用于设置我们想分成几组。

2. 我们学习了 fit_predict(x) 方法，它帮助我们完成数据拟合和预测。

3. 我们使用 calinski_harabasz_score 来评估聚类效果，得分越高，效果越好。

第11页：练习

最后我们来做个练习：

• 下列关于 K-Means API 的描述，哪些是正确的？

• 它是通过 sklearn.cluster.KMeans 实现的。

• 我们可以通过 n_clusters 参数指定数据最终分成几类。

• 右边图中的样本被分为2个类。

正确答案是 A、B、D。

C 选项错误，因为图中样本被分成了2个类，而不是4个类。

KMeans算法实现流程概览

KMeans算法的主要流程可以总结为五个步骤：

1. 确定要分多少类（K值），例如你有一堆客户数据，想把他们分成3组，那K值就是3。

2. 随机选择K个点作为初始聚类中心，这些点会作为开始的“类中心”。

3. 计算每个数据点到K个中心的距离，选择距离最近的中心点，把这个点归类到该类。

4. 重新计算每个类的中心，也就是取所有该类点的平均值作为新的类中心。

5. 反复执行步骤3和步骤4，直到每个类的中心点不再变化。

推理过程：

• 为什么要先确定K值？

因为K值代表了我们希望将数据分为几类。如果数据分成的类过多或者过少，可能导致分类结果过于细化或太宽泛。因此，需要根据实际问题确定合理的K值。

• 为什么需要重复执行计算？

每次分配数据后，类的中心可能会发生变化，为了使结果更精准，KMeans需要反复调整类中心，直到找到最稳定的状态。

KMeans算法示例数据

假设我们有一组二维数据点，它们的坐标如下表所示。每个点有一个X值和Y值，这些数据点就像是在平面上的一些位置，我们现在想通过KMeans算法把它们分成不同的类。

推理过程：

• 什么是二维数据？

二维数据表示每个点有两个属性，比如X代表横坐标，Y代表纵坐标。我们可以把每个点想象成坐标系中的一个点，通过它的两个坐标值确定其位置。

• 这些数据点代表什么？

在实际应用中，这些点可能代表客户的某种行为或特征，比如购买次数和花费金额。我们希望通过KMeans算法发现具有相似行为的客户群体。

选择初始聚类中心点

在这个步骤中，KMeans算法会随机选择K个点作为初始的类中心。例如在这个图中，P1和P2被选为初始中心点。接下来，我们要计算每个数据点到这两个中心点的距离。

图中的公式是欧式距离的计算公式，表示的是两点之间的直线距离，和我们在几何课上学到的“直线距离”一样。

推理过程：

• 欧式距离的计算方法：
欧式距离的公式是 $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$ ，它表示两个点之间的最短路径。这个公式会被用来计算每个数据点到中心点的距离。
• 为什么用距离来分配点？
因为KMeans的核心思想就是“距离近的点应该归为一类”，所以我们通过计算点到中心的距离来确定它属于哪个类。

计算点到中心的距离并分类

现在我们要计算每个数据点到P1和P2两个中心点的距离。表格中展示了P3到P15的所有点分别到P1和P2的距离。例如，P3到P1的距离是1.41，而到P2的距离是6.40，所以P3被分到离P1更近的类中。

通过这样的方式，所有点都被分配到了距离最近的中心点所对应的类。

推理过程：

• 距离近代表相似：

在KMeans算法中，距离是衡量相似度的标准。距离越近，代表这些点越“相似”，所以被分在同一个类。

• 如何确定每个点属于哪个类？

通过比较每个点到所有中心点的距离，选择最小的那个距离，点就归属到距离最小的类中。

重新计算每个类的质心

数据点被分配到不同的类之后，接下来要做的是重新计算每个类的中心点。我们取每个类中所有点的平均值，作为新的质心。例如，P1、P3、P7、P8的平均坐标是(7.3, 7.2)，所以它们的新的质心就是这个坐标。

推理过程：

• 为什么要重新计算质心？
因为在初始阶段，质心是随机选定的，它未必准确代表每个类的中心位置。通过重新计算质心，可以更精确地找到类的中心点，从而更好地分类。
• 如何计算质心？
质心的计算方法是取该类所有点的X值和Y值的平均数。例如，如果类中有3个点，它们的X值分别是3、4、5，Y值分别是6、8、10 那么质心的X坐标就是(3 + 4 + 5) / 3 = 4,那么质心的Y坐标就是(6 + 8 + 10) / 3 = 8, 那么这个类的质心坐标为（4，8）

判断质心是否发生变化

在这个步骤中，算法要判断新的质心是否和上一次计算的质心相同。如果质心不再发生变化，算法就会终止，认为聚类完成。如果质心发生了变化，就需要继续重复前面的步骤，重新分配点，直到质心稳定为止。

推理过程：

• 什么时候算法停止？

当质心不再发生变化时，说明算法找到了最优的分类，每个类的中心已经准确代表了该类的数据，算法就停止。

• 为什么质心会变化？

因为每次重新分配数据点后，类中包含的点会发生变化，因此质心的位置也会发生变化，直到分配稳定下来。

第八页：算法完成，聚类成功

当质心不再变化时，算法认为分类已经完成。图中用椭圆圈出了两个类的分布，红色和蓝色分别代表两个不同的类，每个类中的点都是根据距离和质心的关系进行分配的。

最终结果是：我们成功地将数据点分成了两类，每类的中心点表示了这些点的共同特征。

推理过程：

• 最终的结果代表了什么？

每个类代表了一组相似的数据点，它们有着相似的特征。例如，在客户数据中，这两个类可能代表了两类消费行为相似的客户。

• 如何验证结果？

可以通过可视化或者其他评价指标来验证结果的好坏，确保算法成功将相似的点分到了同一类。

总结：

KMeans算法的实现流程可以总结为以下几个关键步骤：

1. 先决定我们要分成几类，确定K值。

2. 随机选择K个初始中心点。

3. 计算每个点到这些中心点的距离，分配点到最近的类中。

4. 重新计算每个类的质心。

5. 反复执行步骤3和步骤4，直到质心不再变化。

推理过程：

KMeans的核心思想就是“距离决定相似性”，通过迭代优化，算法能够逐步找到最合适的类中心，从而将数据点合理分组。

1. SSE（误差平方和）

背景：

SSE 是 Sum of Squares due to Error 的缩写，中文叫做误差平方和。它是用于衡量每个数据点与其所属簇中心的距离平方之和。在聚类分析中，我们希望相同簇中的点尽可能接近，这样聚类结果才有意义。SSE 就是通过计算点到簇中心的距离来衡量聚类的“紧凑度”。

公式：

$SSE = \sum{i=1}^{k} \sum{p \in C_i} |p - m_i|^2$

( $C_i$ )：表示第 ( i ) 个簇；
( k )：聚类的数量（即多少个簇）；
( p )：簇 ( C_i ) 内的某个点；
( $m_i$ )：第 ( i ) 个簇的质心（簇中心）。

SSE 的作用：

SSE 越小，说明簇内的数据点离它们的质心越近，聚类效果越好。所以在实际操作中，我们希望通过调节聚类的个数 ( k )，让 SSE 尽可能小。

问题的解决：

SSE 用来解决“类内紧密度”的问题。即如何评估某个聚类中数据点是不是足够紧密（同类点聚集在一起）。

数据集示例

假设我们有 10 个样本，并且分为 3 个簇。样本坐标和簇的分配如下：

   •   簇 1： P1(1, 2), P2(2, 3), P3(3, 2), P4(2, 2)
   •   簇 2： P5(6, 8), P6(7, 8), P7(8, 9)
   •   簇 3： P8(10, 1), P9(9, 2), P10(11, 2)

1. SSE（误差平方和）

SSE 衡量每个样本点与其簇中心（质心）之间的距离平方的总和。SSE 越小，表示数据点越接近它们的中心，聚类效果越好。

第一步：计算每个簇的质心

• 簇 1 的质心：

$C_1 = \left( \frac{1+2+3+2}{4}, \frac{2+3+2+2}{4} \right) = (2, 2.25)$

• 簇 2 的质心：

$C_2 = \left( \frac{6+7+8}{3}, \frac{8+8+9}{3} \right) = (7, 8.33)$

• 簇 3 的质心：

$C_3 = \left( \frac{10+9+11}{3}, \frac{1+2+2}{3} \right) = (10, 1.67)$

第二步：计算每个点与其簇质心的平方距离

我们使用欧几里得距离公式计算每个点与质心的距离平方：

   •   簇 1：
   •   P1(1, 2) 到 $C_1$ ： $(1 - 2)^2 + (2 - 2.25)^2 = 1 + 0.0625 = 1.0625$
   •   P2(2, 3) 到 $C_1$ ： $(2 - 2)^2 + (3 - 2.25)^2 = 0 + 0.5625 = 0.5625$
   •   P3(3, 2) 到 $C_1$ ： $(3 - 2)^2 + (2 - 2.25)^2 = 1 + 0.0625 = 1.0625$
   •   P4(2, 2) 到 $C_1$ ： $(2 - 2)^2 + (2 - 2.25)^2 = 0 + 0.0625 = 0.0625$

$SSE_1 = 1.0625 + 0.5625 + 1.0625 + 0.0625 = 2.75$

   •   簇 2：
   •   P5(6, 8) 到 $C_2$ ： $(6 - 7)^2 + (8 - 8.33)^2 = 1 + 0.1089 = 1.1089$
   •   P6(7, 8) 到 $C_2$ ： $(7 - 7)^2 + (8 - 8.33)^2 = 0 + 0.1089 = 0.1089$
   •   P7(8, 9) 到 $C_2$ ： $(8 - 7)^2 + (9 - 8.33)^2 = 1 + 0.4489 = 1.4489$

$SSE_2 = 1.1089 + 0.1089 + 1.4489 = 2.6667$

   •   簇 3：
   •   P8(10, 1) 到 $C_3$ ： $(10 - 10)^2 + (1 - 1.67)^2 = 0 + 0.4489 = 0.4489$
   •   P9(9, 2) 到 $C_3$ ： $(9 - 10)^2 + (2 - 1.67)^2 = 1 + 0.1089 = 1.1089$
   •   P10(11, 2) 到 $C_3$ ： $(11 - 10)^2 + (2 - 1.67)^2 = 1 + 0.1089 = 1.1089$

$SSE_3 = 0.4489 + 1.1089 + 1.1089 = 2.6667$
第三步：计算总的 SSE
$SSE = SSE_1 + SSE_2 + SSE_3 = 2.75 + 2.6667 + 2.6667 = 8.0834$

2. 肘部法（Elbow Method）

背景：

肘部法用来确定聚类的最佳个数 ( k )。在聚类问题中，( k ) 是一个关键参数，决定了我们要分成多少个簇，但有时我们并不知道数据应该分多少簇。此时就需要用到肘部法，通过 SSE 的变化来找到一个合理的 ( k )。

解释：

肘部法通过绘制聚类数量 ( k ) 与 SSE 之间的关系图，SSE 会随着 ( k ) 增大而减小。因为簇的数量越多，每个簇的数据点就会越少，SSE 自然会减少。但是，SSE 的减少幅度在某个点之后会变得很小，形成“肘部”形状。这个拐点就是最佳的聚类数。

过程：

从 ( k=1 ) 开始逐步增加簇的数量，计算每个 ( k ) 对应的 SSE。
当 SSE 开始变缓，出现明显的“肘部”时，说明此时的 ( k ) 是最佳聚类数。
继续增加 ( k ) 不会带来明显的聚类改进，反而可能导致过拟合。

问题的解决：

肘部法帮助我们解决了“如何选择最佳的聚类数”的问题，避免了过多或过少的聚类。

from sklearn.cluster import KMeans  # 导入 KMeans 算法，用于聚类
import matplotlib.pyplot as plt  # 导入 matplotlib 的 pyplot 模块，用于数据可视化
from sklearn.datasets import make_blobs  # 导入 make_blobs，用于生成模拟数据集
from sklearn.metrics import calinski_harabasz_score  # 导入 CH 指数（用于聚类评价，但此处未使用）

def dm01_SSE_inertia_plot():
    # 初始化一个空列表，用来存储不同簇数下的 SSE 值
    sse_list = []

    # 使用 make_blobs 生成模拟数据集，1000 个样本，每个样本有 2 个特征，4 个聚类中心
    x, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1, -1], [0, 0], [1, 1], [2, 2]], 
                      cluster_std=[0.4, 0.2, 0.2, 0.2], random_state=22)
    # 参数解释：
    # n_samples=1000：生成 1000 个样本
    # n_features=2：每个样本有 2 个特征（二维数据）
    # centers：指定 4 个中心点，分别为 [-1, -1], [0, 0], [1, 1], [2, 2]
    # cluster_std：指定每个簇的标准差，越小簇内点越集中
    # random_state=22：确保每次生成的数据相同

    # 计算 1 到 99 个簇数下的 SSE 值
    for clu_num in range(1, 100):
        # 初始化 KMeans 模型，指定簇数和最大迭代次数
        my_kmeans = KMeans(n_clusters=clu_num, max_iter=100, random_state=0)
        # 拟合数据
        my_kmeans.fit(x)
        # 将 SSE 值 (inertia) 存入列表
        sse_list.append(my_kmeans.inertia_)

    # 创建一个图像窗口，设置大小为 18x8 英寸，分辨率为 100dpi
    plt.figure(figsize=(18, 8), dpi=100)
    # 设置 x 轴刻度，每隔 3 个单位显示一次
    plt.xticks(range(0, 100, 3), labels=range(0, 100, 3))
    # 显示网格线
    plt.grid(True)
    # 设置图像标题
    plt.title('SSE (Inertia) vs Number of Clusters')
    # 设置 x 轴标签
    plt.xlabel('Number of Clusters')
    # 设置 y 轴标签
    plt.ylabel('SSE (Inertia)')
    # 绘制簇数与 SSE 值的曲线，红色圆圈连接线，markersize=5
    plt.plot(range(1, 100), sse_list, 'or-', markersize=5, label='SSE')
    # 显示图例
    plt.legend(loc='best')
    # 显示生成的图像
    plt.show()

    # 通过观察图像，可以找到 SSE 开始下降趋缓的位置（即肘点），最优的簇数为 4

图片上我们根据肘部法，可以知道图中当K 🟰4 的时候，变化会有较大的差异，因此，我们会选择K=4 即簇为4个来作为我们分类的结果。也就是说最好是聚类成4类。

3. SC（轮廓系数）

背景：

轮廓系数（Silhouette Coefficient，简称 SC）是另一种衡量聚类效果的指标。不同于 SSE 只关注簇内的紧密度，SC 还考虑了簇间的分离度。它结合了簇内点之间的相似度（凝聚度）和不同簇之间的分离度来评价聚类效果。

公式：

$S = \frac{(b - a)}{\max(a, b)}$

( a )：样本到同簇内其他点的平均距离，反映簇内的紧密度；
( b )：样本到最近簇的平均距离，反映簇间的分离度；
SC 的取值范围是 [-1, 1]，SC 越接近 1，说明聚类效果越好。

SC 的作用：

SC 值大：表示簇内的数据点距离较近，同时该点到其他簇的距离较远，聚类效果好。
SC 值小：表示簇内的点距离较远，或者某个点更像属于其他簇，聚类效果差。

问题的解决：

SC 主要用于解决“类内凝聚度与类间分离度的平衡”问题。它既考虑了聚类的紧密性，也考虑了不同簇之间的差异性。

概念复习：

SC（轮廓系数）的公式是：
$SC_i = \frac{(b_i - a_i)}{\max(a_i, b_i)}$

   1.   内聚度 $a_i$ 表示某个点与同簇内其他点的平均距离，内聚度越小，说明该簇内的点分布越紧密，聚类效果越好。
   2.   分离度 $b_i$ 表示某个点到最近的其他簇内所有点的平均距离（⚠️注意：只要最近那个的值），分离度越大，说明簇间的分离效果越好。
   •   $a_i$ 是点 i 的内聚度。
   •   $b_i$ 是点 i 的分离度。
   •   取值范围：[-1, 1]，SC 越接近 1，说明聚类效果越好。

通过 $SC_i$ 公式可知，这个公式是计算每个i点的轮廓系数值，也就是说每一个点i都会计算出一个 $SC_i$ 值，但是一个点的 $SC_i$ 值无法评估模型聚类的能力，所以我们会计算所有样本点的平均 $SC_i$ 值，即每个点的 $SC_i$ 值相加，然后除以样本个数。这也是代码中SC（轮廓系数）的计算公式。

# 导入必要的库
from sklearn.cluster import KMeans  # 导入 KMeans 聚类算法
import matplotlib.pyplot as plt  # 导入 matplotlib 用于绘图
from sklearn.datasets import make_blobs  # 导入 make_blobs 用于生成模拟数据
from sklearn.metrics import silhouette_score  # 导入 silhouette_score 用于计算轮廓系数

# 定义函数来计算不同簇数下的轮廓系数
def dm02_silhouette_coefficient():
    silhouette_list = []  # 初始化一个空列表，用于存储每个簇数下的轮廓系数

    # 生成模拟数据集
    # n_samples=1000 生成1000个样本
    # n_features=2 表示每个样本有2个特征（二维数据）
    # centers 指定了4个聚类中心，分别为 [-1, -1], [0, 0], [1, 1], [2, 2]
    # cluster_std 指定每个聚类的标准差，数值越小簇内点越集中
    x, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1, -1], [0, 0], [1, 1], [2, 2]],
                      cluster_std=[0.4, 0.2, 0.2, 0.2], random_state=22)  # 固定随机种子使每次生成的数据一致

    # 计算不同簇数下的轮廓系数
    for clu_num in range(2, 100):  # 从2个簇开始，计算到99个簇
        # 初始化 KMeans 模型，指定簇数和最大迭代次数
        my_kmeans = KMeans(n_clusters=clu_num, max_iter=100, random_state=0)
        # 拟合模型，对数据进行聚类
        my_kmeans.fit(x)
        # 预测簇标签
        cluster_labels = my_kmeans.predict(x)
        # 计算轮廓系数并添加到列表中，轮廓系数衡量了聚类结果的优劣
        silhouette_list.append(silhouette_score(x, cluster_labels))

    # 绘制轮廓系数随簇数变化的图
    plt.figure(figsize=(18, 8), dpi=100)  # 设置图像大小和分辨率
    plt.xticks(range(0, 100, 3), labels=range(0, 100, 3))  # 设置 x 轴刻度
    plt.grid(True)  # 显示网格线
    plt.title('Silhouette Coefficient vs. Number of Clusters')  # 设置图像标题
    plt.xlabel('Number of Clusters')  # 设置 x 轴标签
    plt.ylabel('Silhouette Coefficient')  # 设置 y 轴标签
    # 绘制簇数与轮廓系数的曲线，'ob-' 表示蓝色圆圈连接线
    plt.plot(range(2, 100), silhouette_list, 'ob-', markersize=5, label='Silhouette Coefficient')
    plt.legend(loc='best')  # 显示图例
    plt.show()  # 显示图像

    # 通过观察图像，可以找到轮廓系数达到最大值的位置，该位置通常是最优的簇数

# 调用函数进行计算并绘图
dm02_silhouette_coefficient()

数据集示例

计算公式：

$SC_i = \frac{b_i - a_i}{\max(a_i, b_i)}$

为了更清晰地解释如何计算每个样本的分离度 $a_i$ 和轮廓系数 $b_i$ ，以及轮廓系数SC我们通过一个例子来详细说明。

例子：计算样本的分离度和轮廓系数

假设我们有以下三个簇的二维数据点：
- 簇 1： $( P_1(1, 2), P_2(2, 3), P_3(3, 2) )$
- 簇 2： $( P_4(6, 8), P_5(7, 8), P_6(8, 9) )$
- 簇 3： $( P_7(10, 1), P_8(9, 2), P_9(11, 2) )$
我们要计算样本 $P_1(1, 2)$ 的凝聚度、分离度和轮廓系数，并说明整个计算过程（注意本次只计算一个点的值，其他点计算凝聚度、分离度和轮廓系数是一样过程，最好计算SC 的时候，求了所有点的平均值轮廓系数SC ）。

第一步：计算凝聚度 ( $a_i$ )

凝聚度 ( $a_i$ ) 是样本 (i) 到所属簇中所有其他样本的平均距离。
- ( $P_1$ ) 属于簇 1，簇 1 中的其他样本是 $P_2(2, 3)$ 和 $P_3(3, 2)$ 。
- 计算 ( $P_1$ ) 到簇内其他样本的距离：
  - 到 $P_2(2, 3)$ 的距离： $\sqrt{(2 - 1)^2 + (3 - 2)^2} = \sqrt{1 + 1} = \sqrt{2} \approx 1.41$
  - 到 $P_3(3, 2)$ 的距离： $\sqrt{(3 - 1)^2 + (2 - 2)^2} = \sqrt{4 + 0} = \sqrt{4} = 2$
凝聚度 ( $a_1$ )： $a_1 = \frac{1.41 + 2}{2} = 1.71$

第二步：计算分离度 ( $b_i$ )

分离度 ( $b_i$ ) 是样本 (i) 到最近的其他簇的平均距离。
- ( $P_1$ ) 的最近簇是簇 2和簇 3，我们需要分别计算它到这两个簇的平均距离，然后选择距离最小的那个簇。
计算 (P_1) 到簇 2 的距离：
- 到 $P_4(6, 8)$ ： $\sqrt{(6 - 1)^2 + (8 - 2)^2} = \sqrt{25 + 36} = \sqrt{61} \approx 7.81$
- 到 $P_5(7, 8)$ ： $\sqrt{(7 - 1)^2 + (8 - 2)^2} = \sqrt{36 + 36} = \sqrt{72} \approx 8.49$
- 到 $P_6(8, 9)$ ： $\sqrt{(8 - 1)^2 + (9 - 2)^2} = \sqrt{49 + 49} = \sqrt{98} \approx 9.90$
簇 2 的平均距离： $b_1^{(2)} = \frac{7.81 + 8.49 + 9.90}{3} = \frac{26.2}{3} \approx 8.73$

计算 $P_1$ 到簇 3 的距离：
- 到 $P_7(10, 1)$ ： $\sqrt{(10 - 1)^2 + (1 - 2)^2} = \sqrt{81 + 1} = \sqrt{82} \approx 9.06$
- 到 $P_8(9, 2)$ ： $\sqrt{(9 - 1)^2 + (2 - 2)^2} = \sqrt{64} = 8$
- 到 $P_9(11, 2)$ ： $\sqrt{(11 - 1)^2 + (2 - 2)^2} = \sqrt{100} = 10$
簇 3 的平均距离： $[ b_1^{(3)} = \frac{9.06 + 8 + 10}{3} = \frac{27.06}{3} \approx 9.02 ]$

选择最近的簇：

分离度 $(b_1)$ 为 $(b_1 = \min(b_1^{(2)}, b_1^{(3)}) = \min(8.73, 9.02) = 8.73)$ ，因此簇 2是 $(P_1)$ 最近的簇。
即 $P_1$ 点的分离度 $(b_1)$ 为 8.73

第三步：计算轮廓系数 $(SC_i)$

轮廓系数 $(SC_i)$ 的公式是： $[ SC_i = \frac{b_i - a_i}{\max(a_i, b_i)} ]$

对于 $(P_1)$ 来说：
- 凝聚度 $(a_1 = 1.71)$
- 分离度 $(b_1 = 8.73)$
代入公式： $[ SC_1 = \frac{8.73 - 1.71}{\max(1.71, 8.73)} = \frac{7.02}{8.73} \approx 0.80 ]$

总结：
- 凝聚度 $(a_1 = 1.71)$ 表示 $(P_1)$ 与簇 1 中其他点的平均距离。
- 分离度 $(b_1 = 8.73)$ 表示 $(P_1$ ) 与最近簇（簇 2）的平均距离。
- 轮廓系数 $(SC_1 = 0.80)$ ，表示样本 $(P_1)$ 聚类效果较好，值接近 1，说明它更好地属于它所在的簇。
整体聚类模型的轮廓系数：

对所有样本的轮廓系数 $(SC_i)$ 计算后取平均，就可以得出聚类模型的整体轮廓系数，用来衡量聚类效果。

轮廓系数（Silhouette Coefficient，SC）的取值范围是 ([-1, 1])，这是因为它通过比较样本的凝聚度和分离度来衡量聚类效果。我们可以通过公式和直观解释来理解为什么它的取值范围是 $([-1, 1])$

轮廓系数的公式

轮廓系数 ( $SC_i$ ) 的计算公式为： $[ SC_i = \frac{b_i - a_i}{\max(a_i, b_i)} ]$ 其中：

$(a_i)$ 是样本 (i) 的凝聚度，即样本与其所属簇内其他样本的平均距离。
$(b_i)$ 是样本 (i) 的分离度，即样本与最近的其他簇的平均距离。

公式中的 $(SC_i)$ 用来衡量样本 (i) 是更接近它的自身簇，还是更接近最近的其他簇。

为什么取值在 ([-1, 1]) 之间？

当 $(SC_i = 1)$ 时：此时 $(a_i)$ 很小（样本与其所在簇内其他样本非常接近），而 $(b_i)$ 很大（样本与最近的其他簇的平均距离很远）。这是理想的情况，说明样本点与自己的簇高度匹配，并且远离其他簇，聚类效果非常好。
当 ( $SC_i = 0$ ) 时：此时 $(a_i$ ) 和 ( $b_i$ ) 相等，意味着样本点与它所在簇的其他点的距离和它与最近的其他簇的距离差不多。这表示样本点位于簇的边界，聚类效果不明显。
当 ( $SC_i = -1$ ) 时：此时 $(a_i > b_i)$ ，意味着样本点与其他簇的距离比与自己簇的距离更近，说明样本可能被错误地分配到了当前簇。这是最糟糕的情况，表示样本应该属于另一个簇。

取值范围的直观解释

当 ( $SC_i = 1$ )，说明样本与自己簇的其他样本非常接近，与其他簇的样本距离较远，表明聚类效果很好。
当 ( $SC_i = 0$ )，说明样本位于簇的边界，聚类效果中等，样本点无法明显区分到底更应该属于哪个簇。
当 ( $SC_i = -1$ )，说明样本距离其他簇的样本比自己簇的样本还要近，表明聚类效果很差，样本可能被错误归类。

因此，轮廓系数的范围 ([-1, 1]) 可以很好地反映聚类效果的好坏，从非常差（接近 -1）到非常好（接近 1）。

下面是描述过程，不过我理解上面应该很好的描述了计算过程：
计算凝聚度 ( $a_i$ ) 的流程如下：

凝聚度 (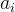 $a_i$ ) 是什么？

凝聚度 ( $a_i$ ) 是样本 (i) 与其所属簇内其他所有样本的平均距离。它反映了样本 (i) 在其所属簇内的紧密程度。凝聚度越小，表示样本与同一簇内其他样本越接近，簇内的聚类效果越好。

计算凝聚度 (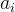 $a_i$ ) 的步骤：

找到样本 ( $P_i$ ) 所属的簇：首先确定样本 ( $P_i$ ) 所属的簇（即由聚类算法划分出的簇）。
计算样本 ( $P_i$ ) 到同一簇内其他样本的距离：
- 记 ( $C_k$ ) 为样本 ( $P_i$ ) 所在的簇（簇 (k)），该簇包含 ( $N_k$ ) 个样本。
- 对于 ( $P_i$ ) 所属的簇 ( $C_k$ )，计算 ( $P_i$ ) 到该簇内每个其他样本的距离。这些距离是欧氏距离（或者根据情况使用其他距离度量）。
求出簇内样本的平均距离：
- 将所有的距离求和，并除以簇内样本的总数减去 1（因为不包含样本自身）。公式如下：
$[ a_i = \frac{1}{N_k - 1} \sum_{P_j \in C_k, j \neq i} d(P_i, P_j) ]$

其中，( $d(P_i, P_j)$ ) 表示样本 ( $P_i$ ) 与样本 ( $P_j$ ) 之间的距离，( $N_k$ ) 是簇 ( $C_k$ ) 中的样本总数。

示例：

假设我们有一个样本 ( $P_1$ ) 位于簇 ( $C_k$ ) 中，而 ( $C_k$ ) 由 4 个样本 ( $P_1, P_2, P_3, P_4$ ) 组成。我们要计算样本 ( $P_1$ ) 的凝聚度 ( $a_1$ )。

计算 ( $P_1$ ) 到 ( $P_2$ )、( $P_1$ ) 到 ( $P_3$ )、( $P_1$ ) 到 ( $P_4$ ) 的距离。
将这些距离相加，并除以簇内的样本总数减 1（即 (3)）：

$[ a_1 = \frac{d(P_1, P_2) + d(P_1, P_3) + d(P_1, P_4)}{3} ]$
上面就得到了 $P_1$ 点的凝聚度 ( $a_1$ )（划重点，是P1点的，不是整个模型的）