用独立分量分析分离混合信号

周围的世界是来自各种来源的信号的动态混合。就像上面图片中的颜色相互融合，产生新的色调和色调一样，我们感知的一切都是简单组件的融合。大多数时候，我们甚至都不知道我们周围的世界是如此混乱的独立过程混合。只有在不同的刺激，不能很好地混合，争夺我们的注意力的情况下，我们才能意识到这种混乱。一个典型的例子是鸡尾酒会上的场景，其中一个人正在聆听另一个人的声音，同时过滤掉所有其他客人的声音。根据房间的响度，这可能是一项简单或艰巨的任务，但不知何故，我们的大脑能够将信号与噪音分开。虽然不了解我们的大脑如何进行这种分离，但有几种计算技术旨在将信号分解为其基本组件。其中一种方法称为独立分量分析（ICA），在这里我们将仔细研究该算法的工作原理以及如何在Python代码中将其写下来。如果您对代码比对解释更感兴趣，您也可以直接查看the Jupyter Notebook for this post on Github.

What is Independent Component Analysis?

让我们暂时留下鸡尾酒会的榜样。 成像有两个人说话，你可以听到他们两个，但一个比你更接近你。 两个声源的声波将混合并作为组合信号到达您的耳朵。 你的大脑会混合两个来源，你会分别感知两个客人的声音，一个人站在离你更近的声音。 现在让我们以更抽象和简化的方式描述它。 每个源都是具有恒定频率的正弦波。 两种来源都取决于你所处的位置。 这意味着更接近你的源在混合信号中将比在更远的地方更占优势。 我们可以在向量矩阵表示法中将其写成如下：

其中x是观测信号，s是源信号，A是混合矩阵。 换句话说，我们的模型假设信号x是通过源信号的线性组合产生的。 在Python代码中，我们的示例如下所示：

>> import numpy as np

>>> # Number of samples 
>>> ns = np.linspace(0, 200, 1000)

>>> # Sources with (1) sine wave, (2) saw tooth and (3) random noise
>>> S = np.array([np.sin(ns * 1), 
                  signal.sawtooth(ns * 1.9),
                  np.random.random(len(ns))]).T

>>> # Quadratic mixing matrix
>>> A = np.array([[0.5, 1, 0.2],
                  [1, 0.5, 0.4],
                  [0.5, 0.8, 1]])

>>> # Mixed signal matrix
>>> X = S.dot(A).T

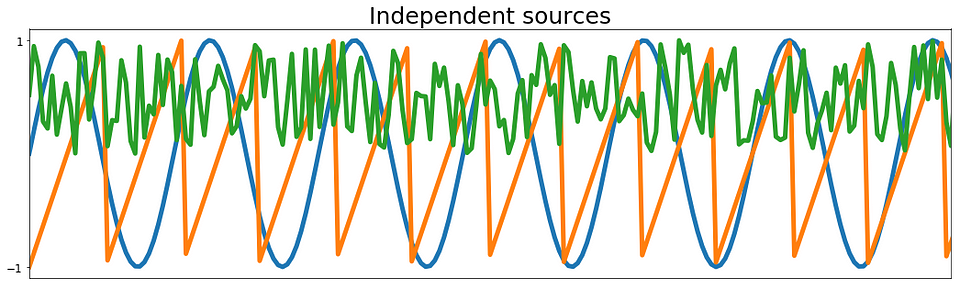
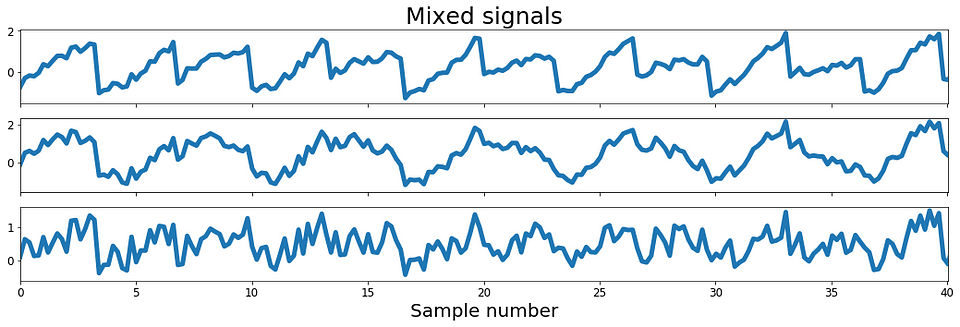
从下面图1中的图中可以看出，代码生成一个正弦波信号，一个锯齿信号和一些随机噪声。 这三个信号是我们的独立来源。 在下图中，我们还可以看到源信号的三个线性组合。 此外，我们看到第一混合信号由锯齿分量支配，第二混合信号更多地受到正弦波分量的影响，而最后的混合信号则受噪声分量的支配。

现在，根据我们的模型，我们可以通过将x乘以A的倒数从混合信号中再次检索源信号：

这意味着为了找到我们需要计算W的源信号。所以本文其余部分的任务是找到W并从两个混合信号中检索两个独立的源信号。

Preconditions for the ICA to work

现在，在我们继续之前，我们需要更多地考虑源信号需要具有哪些属性，以便ICA成功估计W.算法工作的第一个前提条件是混合信号是任意数量的线性组合。源信号。第二个前提条件是源信号是独立的。独立意味着什么呢？如果信号s1中的信息没有给出关于信号s2的任何信息，则两个信号是独立的。这意味着它们没有相关性，这意味着它们的协方差为0.但是，在这里必须要小心，因为不相关性并不自动意味着独立性。第三个前提条件是独立分量是非高斯分量。这是为什么？两个独立的非高斯信号的联合密度分布在正方形上是均匀的;见下图2中的左上图。将这两个信号与正交矩阵混合将导致两个信号现在不再独立并且在平行四边形上具有均匀分布;参见图2右上图。这意味着如果我们处于混合信号之一的最小值或最大值，我们就知道另一个信号的值。因此他们不再独立。对两个高斯信号执行相同操作将产生其他信息（参见图2的下图）。源信号的联合分布是完全对称的，混合信号的联合分布也是如此。因此，它不包含任何有关混合矩阵的信息，我们想要计算它的倒数。因此，在这种情况下，ICA算法将失败。

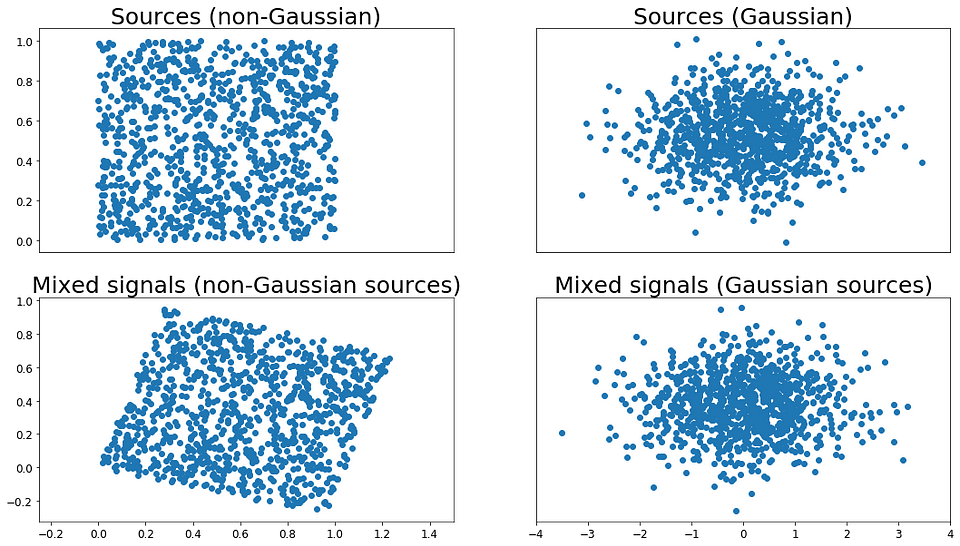
Figure 2: 高斯和非高斯源及其混合物

因此，总而言之，要使ICA算法工作，需要满足以下前提条件：我们的源是（2）独立的（3）非高斯信号的（1）线性混合。

因此，我们快速检查上面的测试信号是否符合这些前提条件。 在下面的左图中，我们看到针对锯齿信号的正弦波信号绘图，而每个点的颜色代表噪声分量。 对于非高斯随机变量，信号按预期分布在正方形上。 同样地，混合信号在图3的右图中形成平行四边形，其示出混合信号不再是独立的。

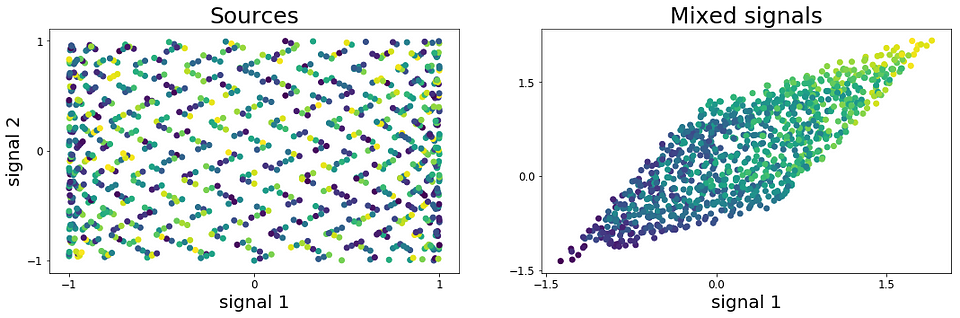
Figure 3: 源和混合信号的散点图

Pre-processing steps

现在采取混合信号并将它们直接送入ICA并不是一个好主意。 为了获得独立组件的最佳估计，建议对数据进行一些预处理。 在下文中，更详细地解释了两种最重要的预处理技术。

Centering

我们将在这里讨论的第一个预处理步骤是居中。 这是从输入X的平均值的简单减法。因此，居中的混合信号将具有零均值，这意味着我们的源信号s也是零均值。 这简化了ICA计算，以后可以加回平均值。 Python中的中心函数如下所示。

>>> def center(x):
>>>     return x - np.mean(x, axis=1, keepdims=True)

Whitening

我们需要的第二个预处理步骤是对信号X进行白化。这里的目标是线性变换X，以便消除信号之间的潜在相关性，并使它们的方差等于1。 结果，白化信号的协方差矩阵将等于单位矩阵：

我在哪里是单位矩阵。 由于我们还需要在白化过程中计算协方差，我们将为它编写一个小的Python函数。

>>> def covariance(x):
>>>     mean = np.mean(x, axis=1, keepdims=True)
>>>     n = np.shape(x)[1] - 1
>>>     m = x - mean
>>> return (m.dot(m.T))/n

美白步骤的代码如下所示。 它基于X的协方差矩阵的奇异值分解（SVD）。如果您对此过程的细节感兴趣，我建议 this article.

>>> def whiten(x):
>>>     # Calculate the covariance matrix
>>>     coVarM = covariance(X) 

>>>     # Singular value decoposition
>>>     U, S, V = np.linalg.svd(coVarM)
    
>>>     # Calculate diagonal matrix of eigenvalues
>>>     d = np.diag(1.0 / np.sqrt(S)) 
    
>>>     # Calculate whitening matrix
>>>     whiteM = np.dot(U, np.dot(d, U.T))
    
>>>     # Project onto whitening matrix
>>>     Xw = np.dot(whiteM, X) 
    
>>>     return Xw, whiteM

Implementation of the FastICA Algorithm

好了，现在我们已经有了预处理功能，我们终于可以开始实现ICA算法了。基于测量独立性的对比度函数，有几种实现ICA的方法。在这里，我们将在名为FastICA的ICA版本中使用近似的negentropy。

那么它是怎样工作的？如上所述，ICA工作的一个前提是我们的源信号是非高斯信号。关于两个独立的非高斯信号的一个有趣的事情是它们的和比任何源信号更高斯。因此，我们需要以Wx的结果信号尽可能不高斯的方式优化W.为了做到这一点，我们需要一种高斯度量。最简单的衡量标准是峰度，这是数据的第四个时刻，它衡量的是分布的“尾部”。正态分布的值为3，均匀分布就像我们在图2中使用的那样具有峰度<3。Python中的实现是直截了当的，从下面的代码可以看出，它也计算了数据的其他时刻。第一个时刻是平均值，第二个是方差，第三个是偏度，第四个是峰度。这里从第四时刻中减去3，使得正态分布的峰度为0。

>>> def kurtosis(x):
>>>     n = np.shape(x)[0]
>>>     mean = np.sum((x**1)/n) # Calculate the mean
>>>     var = np.sum((x-mean)**2)/n # Calculate the variance
>>>     skew = np.sum((x-mean)**3)/n # Calculate the skewness
>>>     kurt = np.sum((x-mean)**4)/n # Calculate the kurtosis
>>>     kurt = kurt/(var**2)-3

>>> return kurt, skew, var, mean

对于我们实施的ICA，我们不会使用峰度作为对比函数，但我们可以稍后使用它来检查我们的结果。 相反，我们将使用以下对比函数g（u）及其一阶导数g’（u）：

FastICA算法在[定点迭代方案]中以下列方式使用上述两个函数(https://homepage.math.uiowa.edu/~whan/072.d/S3-4.pdf):

因此，根据上述内容，我们要做的是随机猜测每个组件的权重。 随机权重和混合信号的点积被传递到两个函数g和g’中。 然后我们从g中减去g’的结果并计算平均值。 结果是我们的新权重向量。 接下来，我们可以直接将新权重向量除以其范数，并重复上述步骤，直到权重不再变化为止。 这没有什么不妥。 然而，我们在这里面临的问题是，在第二个组件的迭代中，我们可能会识别与第一个迭代中相同的组件。 为了解决这个问题，我们必须从先前确定的权重中去除新的权重。 这是在更新权重和除以其规范之间的步骤中发生的事情。 在Python中，实现看起来如下：

>>> def fastIca(signals,  alpha = 1, thresh=1e-8, iterations=5000):
>>>     m, n = signals.shape

>>>     # Initialize random weights
>>>     W = np.random.rand(m, m)

>>>     for c in range(m):
>>>             w = W[c, :].copy().reshape(m, 1)
>>>             w = w/ np.sqrt((w ** 2).sum())

>>>             i = 0
>>>             lim = 100
>>>             while ((lim > thresh) & (i < iterations)):

>>>                 # Dot product of weight and signal
>>>                 ws = np.dot(w.T, signals)

>>>                 # Pass w*s into contrast function g
>>>                 wg = np.tanh(ws * alpha).T

>>>                 # Pass w*s into g'
>>>                 wg_ = (1 - np.square(np.tanh(ws))) * alpha

>>>                 # Update weights
                    wNew = (signals * wg.T).mean(axis=1) - 
>>>                         wg_.mean() * w.squeeze()

>>>                 # Decorrelate weights              
>>>                 wNew = wNew - 
                           np.dot(np.dot(wNew, W[:c].T), W[:c])
>>>                 wNew = wNew / np.sqrt((wNew ** 2).sum())

>>>                 # Calculate limit condition
>>>                 lim = np.abs(np.abs((wNew * w).sum()) - 1)
                
>>>                 # Update weights
>>>                 w = wNew
                
>>>                 # Update counter
>>>                 i += 1

>>>             W[c, :] = w.T
>>>     return W

所以现在我们已经编写了所有代码，让我们运行整个事情！

>>> # Center signals
>>> Xc, meanX = center(X)

>>> # Whiten mixed signals
>>> Xw, whiteM = whiten(Xc)

>>> # Run the ICA to estimate W
>>> W = fastIca(Xw,  alpha=1)

>>> #Un-mix signals using W
>>> unMixed = Xw.T.dot(W.T)

>>> # Subtract mean from the unmixed signals
>>> unMixed = (unMixed.T - meanX).T

ICA的结果如下图4所示，其中上面板代表原始源信号，下面板是我们的ICA实现检索的独立元件。 结果看起来非常好。 我们得到了所有三个来源！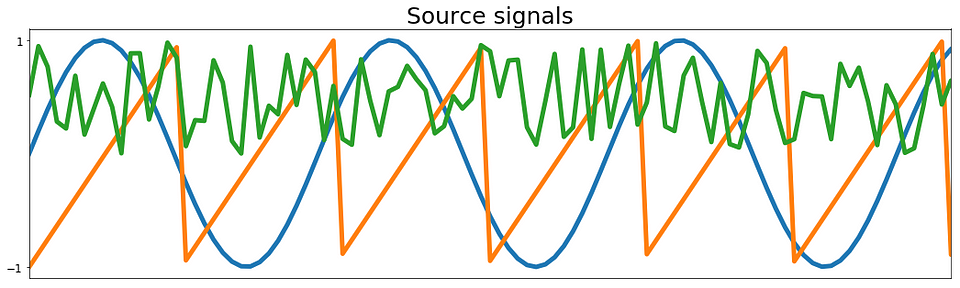
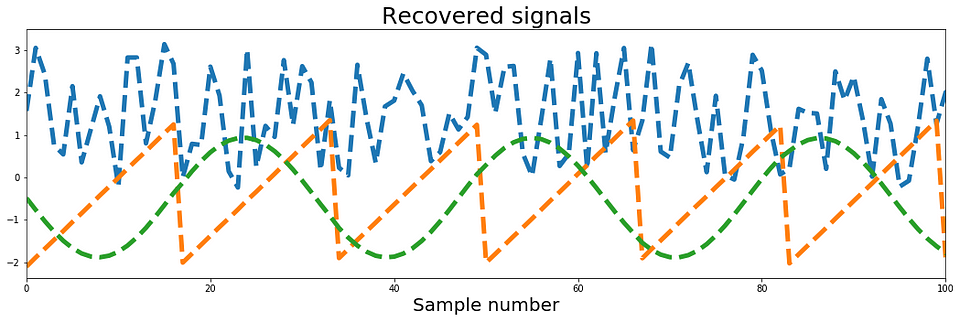
图4：ICA分析的结果。 以上真实来源; 低于恢复信号。

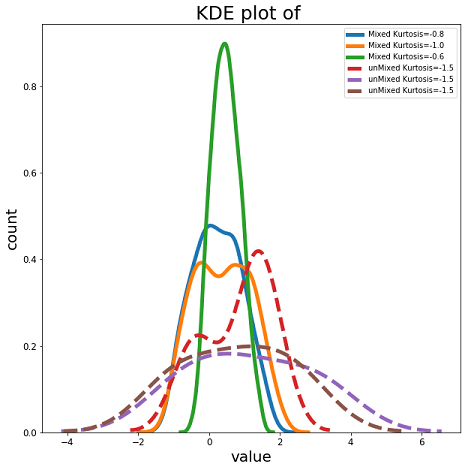
所以最后让我们检查最后一件事：信号的峰度。 正如我们在图5中可以看到的，我们所有混合信号的峰度≤1，而所有恢复的独立分量都具有1.5的峰度，这意味着它们的高斯低于其源。 这必须是这种情况，因为ICA试图最大化非高斯性。 此外，它很好地说明了上面提到的事实，非高斯信号的混合将比源更高斯。

总结一下：我们看到了ICA如何工作以及如何在Python中从头开始实现它。 当然，有许多可用的Python实现可以直接使用。 但是，总是可以理解该方法的基本原理，以了解何时以及如何使用它。 如果您有兴趣深入了解ICA并了解我推荐的细节本文由AapoHyvärinen和Erkki Oja撰写，2000.

否则你可以在这里查看完整的代码，在Twitter上关注我或通过连接 LinkedIn.

可以在上找到该项目的代码 Github.
`