提炼总结—机器人学导论（原书第四版）（第2章）

写在最前面的话

为什么做该博客？该博客的特点是什么？
随着DeepSeek、ChatGPT等AI技术的崛起，促使机器人技术发展到了新的高度，诞生了宇树科技、特斯拉为代表的人形机器人，四足机器人等等，越来越多的科技巨头涌入机器人赛道，行业对于相关人才的需求也随之达到了顶峰。本博客的内容是替你阅读所有关于机器人的经典书籍，采用书籍瘦身计划，帮你提炼出核心内容，采用最通俗易懂的语言来解释原理，将书读薄。大大缩短学习时间，助你快速成为机器人时代的佼佼者。

---

---

一、书籍介绍

《机器人学导论（原书第4版）》是约翰·J·克雷格的经典教材，系统讲解机器人运动学、动力学与控制理论，结合MATLAB实践，适合本科高年级与研究生学习。新增深度学习应用等内容，兼顾基础与前沿。

---

二、第2章 空间描述和变换（提炼总结）

2.1节 引言（提炼总结）

• 世界坐标系：定义的位置和姿态都参照这个坐标系定义
• 笛卡尔坐标系：也叫直角坐标系，它通过一组互相垂直的坐标轴和数值来精确定位点的位置
  举例：
  二维坐标系‌（平面）
  由两条垂直的数轴（x轴横轴、y轴纵轴）相交于原点（0,0）。
  任意点位置用有序数对 ‌(x, y)‌ 表示，例如 (3, 2) 表示向右3单位、向上2单位。
  三维坐标系‌（空间）
  增加第三条垂直的z轴（通常表示高度或深度）。
  点位置用三元组 ‌(x, y, z)‌ 表示，如 (1, -2, 4)。

2.2节 描述：位置、姿态与位姿（提炼总结）

• 位置：表示物体在空间中的坐标点，通常用三维向量描述，(x,y,z)，表示物体在参考坐标系中的线性位移
• 姿态：有三种描述方式
  1、旋转矩阵‌：3×3正交矩阵，列向量为物体坐标系主轴在参考系中的投影。
  
  2、欧拉角‌：(rx,ry,rz)，分别绕X/Y/Z轴的旋转角度（如偏航、俯仰、滚转）
  万向节死锁：当俯仰角为 ±90° 时，偏航和滚转会失去一个自由度，导致旋转异常（如航天器失控），可看上一篇文章的射击飞行员的例子
  ‌3、四元数‌：可以看作‌复数的高维扩展‌，由一个实部和三个虚部组成，其中w表示旋转的角度，（x,y,z）表示旋转轴，通常表示为：
  
  三种表示方法优缺点总结：
  
• 位姿：结合位置和姿态，完整描述物体的空间状态，有两种描述方式
  1、齐次变换矩阵‌：4×4矩阵，整合平移和旋转：
  
  2、位姿向量：(x,y,z,rx,ry,rz)，直接组合位置和欧拉角
• 位置、姿态、位姿关键区别：位置‌仅需3个自由度（坐标值），‌姿态‌需3个旋转参数，而‌位姿‌共需6个自由度（3平移+3旋转）

2.3节 映射：从一个坐标系到另一个坐标系的变换（提炼总结）

• 映射：不同坐标系之间的变换数学方法
• 坐标平移：{A}与{B}的姿态相同，不同的只是平移
  
• 坐标旋转：两个坐标系的原点重合
  
• 一般变换：即坐标旋转+坐标平移
  

2.4节 算子：平移、旋转和变换（提炼总结）

• 算子：用于坐标系间点的映射的通用数学表达式，包括平移算子、矢量旋转算子和平移加旋转算子

2.5节 算子：总结和说明（提炼总结）

• 齐次变换矩阵：用于描述‌刚体运动（旋转+平移）‌的核心数学工具。它将三维空间中的位姿（位置和姿态）统一表示为4×4矩阵形式，便于进行连续的变换计算。
  一个标准的齐次变换矩阵 T 包含以下部分：
  
  ‌为什么叫“齐次”？‌
  引入‌齐次坐标‌（增加一个维度，通常为1），使得非线性变换（如透视投影）也能用线性矩阵表示。
  齐次坐标下，点 (x,y,z)(x,y,z) 表示为 (x,y,z,1)(x,y,z,1)，向量为 (x,y,z,0)(x,y,z,0)。

2.6节 变换的计算（提炼总结）

• 逆变换：已知坐标系{B}相对于坐标系{A}，求坐标系{A}相对于坐标系{B}
  

2.7节 变换方程（提炼总结）

2.8节 其他姿态描述（提炼总结）

• X-Y-Z固定角：将坐标系{B}和一个已知参考坐标系{A}重合，将坐标系{B}绕坐标系{A}的X轴旋转r角（回转角），再绕坐标系{A}的Y轴旋转β角（俯仰角），最后绕坐标系{A}的Z轴旋转α角（偏转角），因为旋转是在固定的参考坐标系{A}确定的，所以叫固定角
  
• Z-Y-X欧拉角：将坐标系{B}和一个已知参考坐标系{A}重合，将坐标系{B}绕坐标系{B}的Z轴旋转α角，再绕坐标系{B}的Y轴旋转β角，最后绕坐标系{B}的X轴旋转r角，每次都是绕运动坐标系{B}的各轴旋转而不是绕固定坐标系{A}的各轴旋转，这样三个一组的旋转称为欧拉角。
  
• Z-Y-Z欧拉角：将坐标系{B}和一个已知参考坐标系{A}重合，将坐标系{B}绕坐标系{B}的Z轴旋转α角，再绕坐标系{B}的Y轴旋转β角，最后绕坐标系{B}的Z轴旋转r角，每次都是绕运动坐标系{B}的各轴旋转而不是绕固定坐标系{A}的各轴旋转，这样三个一组的旋转称为欧拉角。
• 欧拉参数：用于表示三维旋转，避免欧拉角的万向节死锁问题。通常由四个参数组成。欧拉参数本质上是单位四元数

2.9节 自由矢量的变换（提炼总结）

• 线矢量‌：被约束在一条‌固定方向与位置的直线‌上，仅允许沿该直线移动
• 自由矢量‌：可在空间中‌自由平移‌，仅需保持大小和方向不变即视为等价

2.10节 计算问题（提炼总结）

---

三、实战

问题：用Z-Y-X(α-β-γ)欧拉角约定表示法，写出MATLAB程序，当用户输入欧拉角α-β-γ时，计算旋转矩阵。
解答：
1、在matlab中编写如下代码：

function R = euler2rot(angles_deg)
% 输入：angles_deg = [psi, theta, phi]（单位：度）
% 输出：3x3旋转矩阵（Z-Y-X顺序）

psi = deg2rad(angles_deg(1)); % Z轴旋转（偏航角）
theta = deg2rad(angles_deg(2)); % Y轴旋转（俯仰角）
phi = deg2rad(angles_deg(3)); % X轴旋转（滚转角）

Rz = [cos(psi) -sin(psi) 0; sin(psi) cos(psi) 0; 0 0 1];
Ry = [cos(theta) 0 sin(theta); 0 1 0; -sin(theta) 0 cos(theta)];
Rx = [1 0 0; 0 cos(phi) -sin(phi); 0 sin(phi) cos(phi)];

R = Rz * Ry * Rx;
end

2、在命令行窗口输入如下代码：

angles = [30, 45, 60];

R = euler2rot(angles)

3、观察显示结果：对于输入的欧拉角（偏航、俯仰、滚转），得到的旋转矩阵

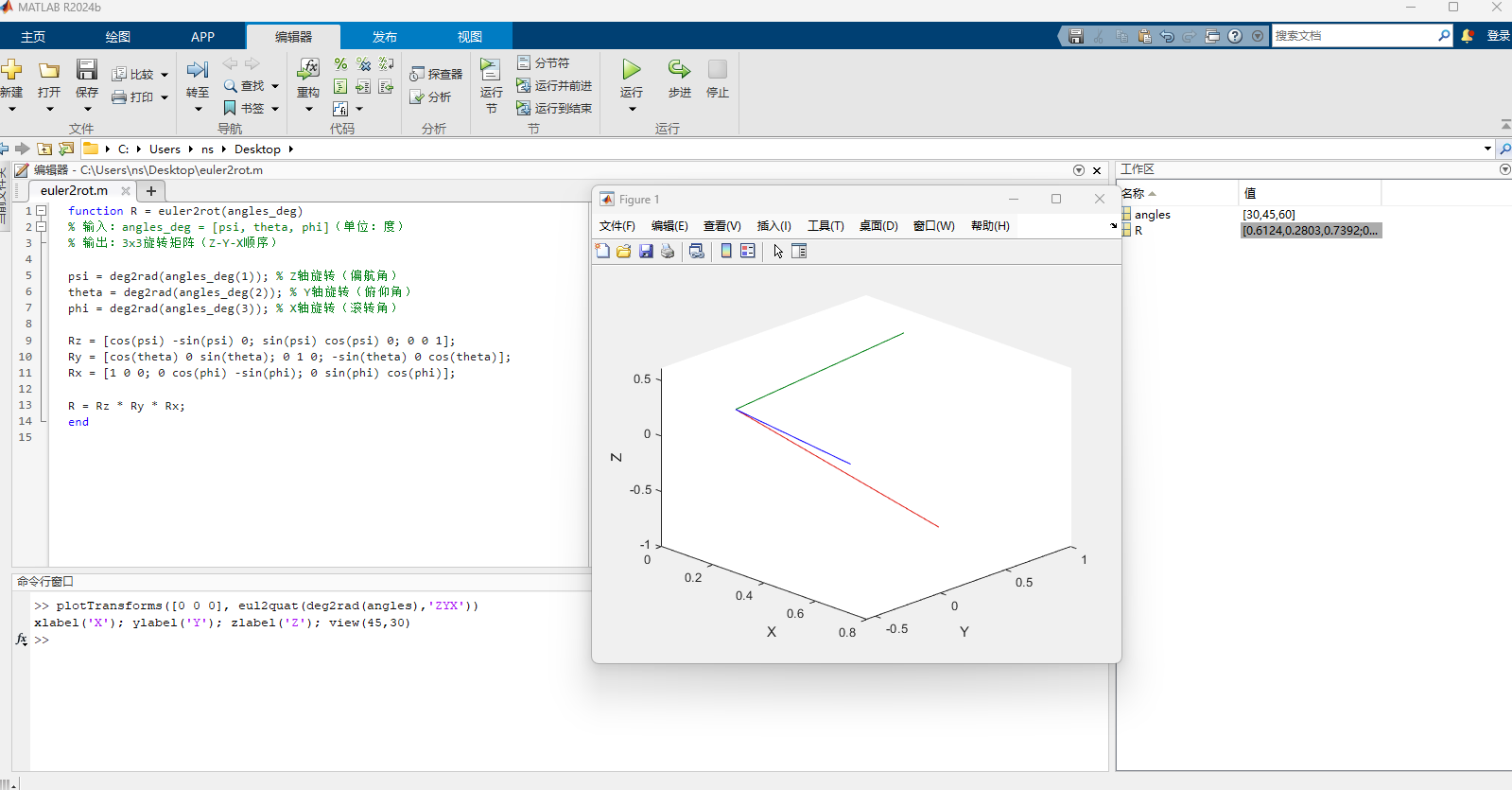
4、可视化显示，在命令行窗口输入：
将显示一个3D坐标系，红色/绿色/蓝色箭头分别对应旋转后的X/Y/Z轴

plotTransforms([0 0 0], eul2quat(deg2rad(angles),'ZYX')) 
xlabel('X'); ylabel('Y'); zlabel('Z'); view(45,30)