Class-Balanced Loss Based on Effective Number of Samples

论文标题：Class-Balanced Loss Based on Effective Number of Samples
会议：CVPR2019
pytorch版代码-GitHub地址：https://github.com/vandit15/Class-balanced-loss-pytorch/blob/master/class_balanced_loss.py
论文下载：https://arxiv.org/pdf/1901.05555.pdf
cifar10的训练代码在另一篇博客中：pytorch+resnet18实现长尾数据集分类

类别不平衡问题

现实世界的数据集，大部分都是分布不均匀的，几个主导类别拥有大量样本，而大多数其他的类别只有着相对较少的样本。使用这种长尾数据集训练CNNs时，模型在弱表示类中表现较差。

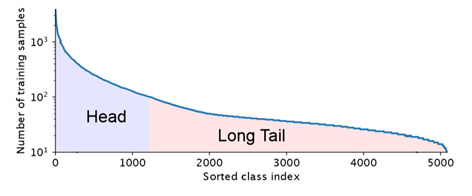
类别不平衡的处理策略：

通常情况下，对于长尾数据集，有以下两种应对策略

1.重新采样  理论及代码链接
    上采样：人工合成/复制数据
    上采样缺点：如果是复制小类样本，新增数据与原数据的特征高度相似，没有本质上的性能提升，容易造成模型过拟合。如果对小类样本进行合成（如SMOTE算法），由于新样本中存在噪声，模型仍然容易出错。
    下采样：按照概率随机抽样，相当于删除大类样本中的一些样本。
    下采样缺点：数据量减少，模型对于多样本类别的分类性能降低。
2.成本敏感学习
在这个方法中，为了匹配给定的数据分布，为样本分配权重。通常采用逆类频率加权或逆类频率的平方根的加权。但是样本难度与样本数量之间并没有直接的联系（比如，A类样本，数据量为2000，但是有1500张数据是类似的；B类样本，数据量为1000，数据都不相同，那么A类样本难度比B类样本难度低），这样简单粗暴的分配权重并没有对数据集的特征进行分析，该方法存在改进空间。

提出问题

如何找到合适的权重赋值方法，提高分类损失函数的效果?

边际效应

随着数据量增加，模型新增的收益越来越少
刚开始接收新数据的时候，网络能够很快学习特征。但是随着数据量的增加，新加入的数据，与之前的已有的数据存在特征重叠，新学到的特征越来越少。

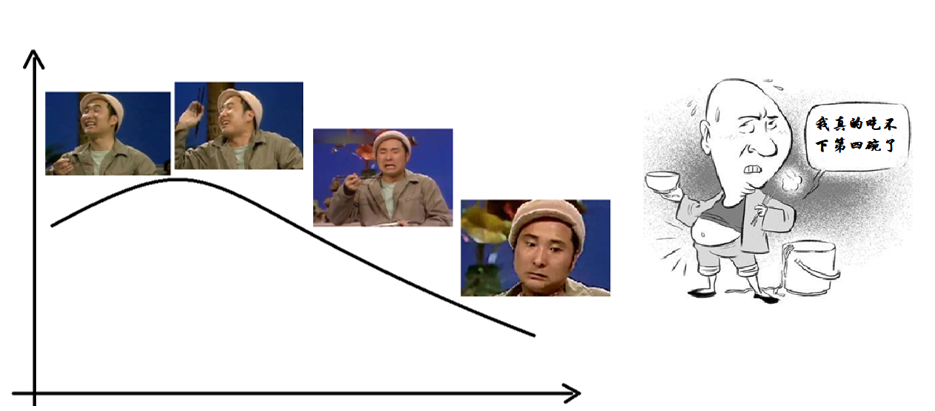
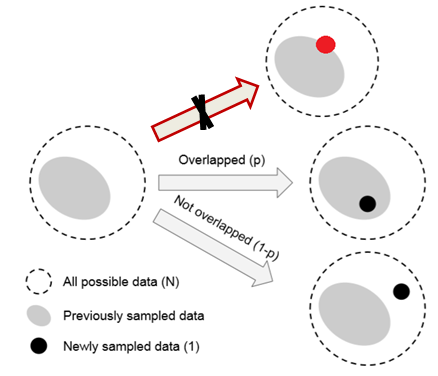
数据采样和随机覆盖

一个类中，该类样本空间中所有可能数据的集合为 $S$。假设，$S$ 的样本体积为 $N$。$S$ 中每个样本的体积都为1，但是由于样本存在特征重叠，所以两个样本的体积满足:1+1<=2。将数据采样过程考虑为一个随机覆盖问题，其中每个数据从 $S$ 中随机抽样以覆盖整个 $S$ 。抽样的数据越多， $S$ 的覆盖越好。采样数据的期望总容量随着数据数量的增加而增加，并以 $N$为界。只要这一段理解了，后面就简单了。

定义

有效样本量是样本的期望体积
之前已经提到过样本体积的概念，样本体积是相对于所有可能数据的集合$S$而言的，$S$为一个理论概念。在真实的样本中，由于存在特征重叠，所以有些样本是多余的，可以通过其他样本得到。这有点类似于线性代数中的极大无关组。我们把那些独一无二的样本的集合称为有效样本量，也就是样本的期望体积。对于独一无二的样本：1+1=2。
注意区分样本的期望体积和样本体积。

命题

计算有效样本量的方法：
提出公式：$E_n=\left(1-{\beta }^n\right)/(1-\beta )$
其中 $n$为样本数量，$N$ 为样本体积，$\beta =(N-1)/N$。
作者使用了数学归纳法证明命题正确。

$n$ 为1时：$E_1=\left(1-{\beta }^1\right)/(1-\beta )=1$

假设 $E_{n-1}=\left(1-{\beta }^{n-1}\right)/(1-\beta )$成立，第 $n$ 个采样数据与前 $n-1$ 个数据重叠的概率为：$p=E_{n-1}/N$
重叠情况下，这 $n$ 个采样数据的样本体积为 $E_{n-1}$；
未重叠情况下，这 $n$ 个采样数据的样本体积为 E n − 1 + 1 E_{n-1} + 1 E