流体力学——流体微团的运动形式与无旋运动的速度势

最新推荐文章于 2024-09-07 15:33:35 发布

hser-chen

最新推荐文章于 2024-09-07 15:33:35 发布

阅读量7.3k

点赞数

分类专栏：流体力学文章标签：流体微团无旋运动势流速度势空间格林定理

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/weixin_41788456/article/details/103768186

版权

流体力学专栏收录该内容

14 篇文章

订阅专栏

概念：

它是由许多流体质点组成的微小流体团，这个微团不仅包含了流体速度、密度、压力等物理量，而且还具有一定的外形。

流体的速度散度表示流体体积变化率：

$\bigtriangledown \cdot V =(\frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial z}) \cdot(u,v,w)=\frac{\partial u }{\partial x}+\frac{\partial v }{\partial y}+\frac{\partial w }{\partial z}$

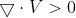$\bigtriangledown \cdot V > 0$ ：表示该流体微团不断有流体流出，称为源（source）

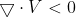$\bigtriangledown \cdot V < 0$ ：表示该流体微团不断吸收流体，称为汇（sink）

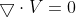$\bigtriangledown \cdot V= 0$ ：表示不可压缩流体的速度场是一个无源场

流体微团的运动形式：

Helmholtz速度分解定理：流体微团的运动速度可以分解为四部分：即（1）平移运动；（2）旋转运动；（3）线变形运动；（4）角变形运动。

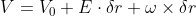
$V=V_{0}+E\cdot \delta r+\omega \times \delta r$

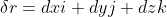
$\delta r=dxi+dyj+dzk$

变形率（张量）：

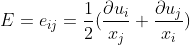
$E=e_{ij}=\frac{1}{2}(\frac{\partial u_{i}}{x_{j}}+\frac{\partial u_{j}}{x_{i}})$

旋转速度（矢量）:

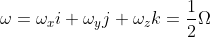
$\omega =\omega _{x}i+\omega _{y}j+\omega _{z}k=\frac{1}{2}\Omega$

无旋运动的速度势

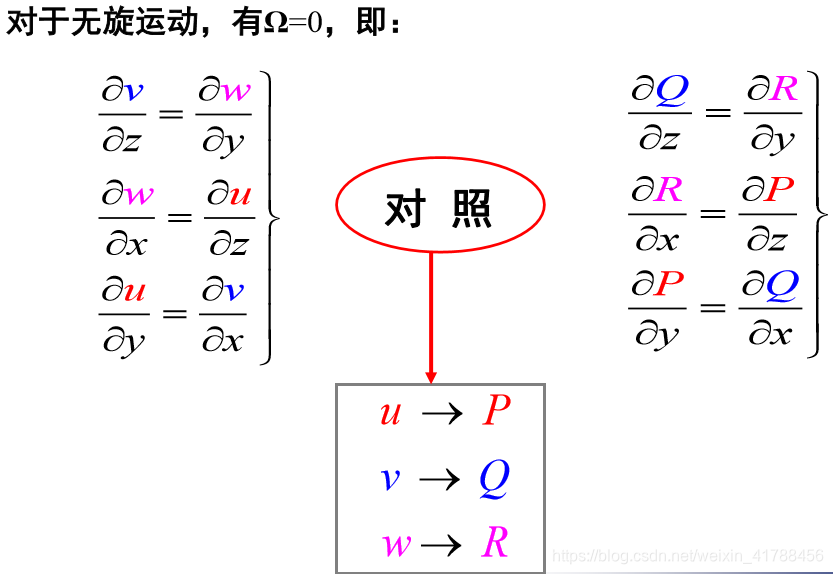
根据流体微团旋转角速度 $\omega$ 或涡量 $\Omega$ 是否为零，可以将流体运动分为有旋运动或无旋运动。

评论 2

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。