目录
1. 原文内容概要
这一章主要是对统计学习(Statistical Learning)里的常见概念进行了细致地讲解,包括:
- 如何用统计学的方式来表达现实世界的数据特征(Phenomenon)?
- 为什么要拟合(Estimate)𝑓(𝑥)?
- 如何去拟合𝑓(𝑥)?
- 在模型解释性(Model Interpretability)和预测精度(Prediction Accuracy)之间如何权衡(Trade-Off)?
- 如何区分监督学习(Supervised Learning)和非监督学习(Unsupervised Learning)?
- 如何区分回归问题(Regression Problems)和分类问题(Classification Problems)?
- 如何去评估(Measuring)模型的质量(the Quality of Fit)?
- 在回归(Regression)和分类(Classification)情景(Setting)下,偏差(Bias)和方差(Variance)如何进行权衡(Trade-Off)?
接下来我会依次讲解上面的问题。

图 1:ISL第二章的目录
2. 算法知识总结
2.1 如何用统计学的方式来表达现实世界的数据特征?
在统计学中,我们一般用 𝑦=𝑓(𝑥)+𝜀 来表达观察到的在数据中蕴含的规律,其中𝑓(𝑥)表示一个由变量𝑋1,𝑋2,𝑋3…𝑋𝑝确定的(fixed),但是又未知的(unknown)的函数(function);𝜀 表示随机的(random),与𝑋1,𝑋2,𝑋3…𝑋𝑝独立的(independent),均值为0(mean zero)的误差项(error term)。
从数学公式的角度,统计学的内容可以简单概括为一句话:用来拟合𝑓(𝑥)的一系列方法。
(In essence, statistical learning refers to a set of approaches for estimating 𝑓)
为啥没有考虑误差𝜀呢?因为这玩意儿实在是囊括了太多的,无法把控的,无法顾及到的因素了,比如:
1)对未考虑到的影响𝑦y的其他变量(光这一点,我们就无能为力了);
2)比如𝑦y是目标对象的血压值,𝜀 还包括了被测量者当时的心理状态(这我们哪能控制呀)。
所以,一般我们就只对𝑓(𝑥)感兴趣,将对 𝑦 的猜想和拟合简化为对𝑓(𝑥)的拟合。
图2很形象地展示了什么是𝑦,什么是𝑓(𝑥),什么是𝜀?
图2表示用教育年限(Years of Education)和资历(Seniority)这两个变量来预测收入(Income)。其中,图中红色的点就代表𝑦,蓝色的面就代表𝑓(𝑥),而红点和蓝色面之间的黑色垂线段就代表误差项𝜀。
⚠️这里请注意下,因为这里关于收入与教育年限和资历关系的数据是本书作者自己模拟的(simulated data),所以𝑓(𝑥)是已知的,因此才能被准确用图画出来。在现实问题中,𝑓(𝑥)的准确形式我们是无从得知的,也无法去精确获取的,只能用已有的数据去模拟它,逼近它,得到𝑓′(𝑥)来代替𝑓(𝑥)。
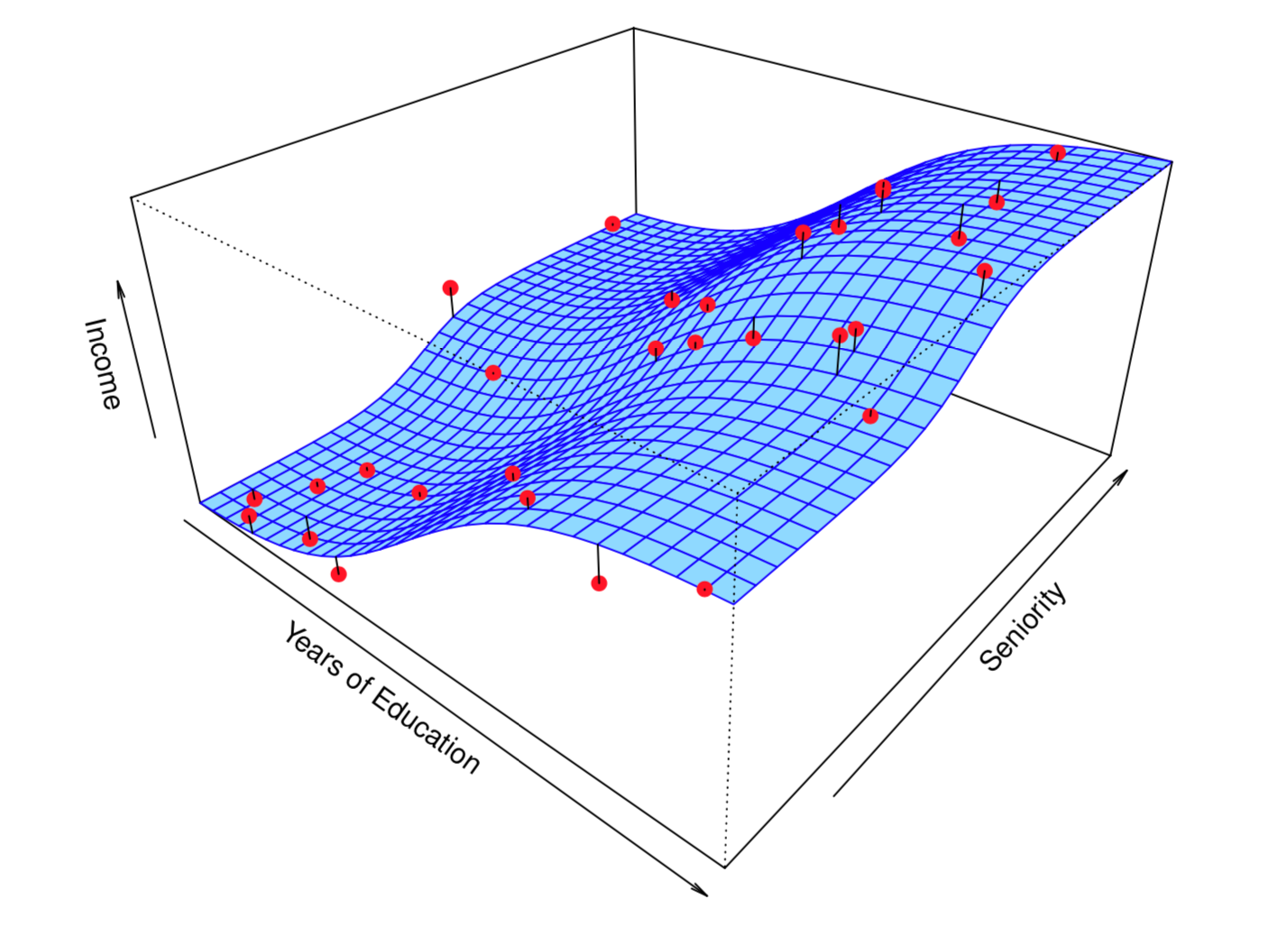
图 2:作者自己模拟的数据,表示收入与教育年限和资历的关系图
2.2 为什么要拟合𝑓(𝑥)?
当我们知道𝑓(𝑥)的概念后,不禁会问,为啥要费尽心思去模拟它呢?
一般来讲,我们拟合𝑓(𝑥)的主要原因分为两种,一种是为了预测(prediction),另一种是为了推论(inference)。(There are two main reasons that we may wish to estimate 𝑓f: prediction and inference)
2.2.1 预测场景
预测的场景一般有哪些呢?比如:股票价值的预测、房价的预测、销售收入的预测。预测场景中,我们一般只关注最终预测值的准确性(accuracy),而对预测的内在逻辑(也就是𝑓(𝑥)的具体形式)并不感兴趣。
2.2.2 推论场景
推论的场景一般有哪些呢?一般来说,我们对一件事情进行推论的时候,会问如下三个依次递进的问题:
1)哪些自变量𝑥与因变量𝑦有关?(Which predictors are associated with the response?)
2)每一个自变量𝑥与因变量𝑦的关系是什么?正向关系还是负向关系?(What is the relationship between the response and each predictor?)
3)这些关系是线性的,还是更复杂的?(Can the relationship between Y and each predictor be adequately summarized using a linear equation, or is the relationship more complicated?)
为了得到上述问题的答案,我们必须清楚地知道𝑓(𝑥)的具体形式,即使这样会牺牲一些预测的精度。
2.2.3 两者结合
当然,在有些任务中,我们既想要预测的准确性(accuracy),又想要可解释性(interpretability),这种场景就是预测和推论的结合了(combination of prediction and inference)。这种情况下,我们就要在𝑓(𝑥)的函数形式复杂度上做一些权衡了,毕竟世上哪有两全法呀。
2.3 如何去拟合𝑓(𝑥)?
一般来说,拟合𝑓(𝑥)的方式分为两种:有参估计法(Parametric methods)和无参估计法(non-parametric methods)。(Most statistical learning methods for this task can be characterized as either parametric or non-parametric)
2.3.1 有参估计法
有参估计法的步骤一般包括以下两步:
1)首先,假设𝑓(𝑥)的具体形式。比如假设它是线性函数,具体形式如下:
![]()
2)然后,选择某种方法(procedure),比如最小二乘法(least squares),用训练数据(train data)去估计(fit)这些参数(parameter),即上面的𝛽0,𝛽1,...,𝛽𝑝。
有参估计法的好处在于,它可以简化拟合𝑓(𝑥)的难度,从拟合𝑓简化到拟合少数参数。(It reduces the problem of estimating 𝑓 down to one of estimating a set of parameters)
有参估计法的不足在于,模型的精度很大程度上取决于我们在第一步中预设的函数形式。万一在第一步中假设𝑓(𝑥)的具体函数形式与实际的真实函数形式差距过大,比如用预设的线性模型去预测非线性的情况,那么即使线性模型里的参数我们预测得多么精准,最终模型的精度也将不忍直视。(The potential disadvantage of a parametric approach is that the model we choose will usually not match the true unknown form of 𝑓)
有一种简单粗暴的方式看似可以解决上述提到的不足,就是在第一步中,一开始就预设非常复杂的函数形式。这种做看似合理,但一般来说也不可取,因为有过拟合(overfitting)的风险。函数形式越复杂,他们就会过于关注数据中那些无足轻重的、甚至干扰的噪音信息,在图像形态上就会表现得过于弯曲、“灵活”(英文一般会说成flexible),这样做反而会让最终模型的精度降低,这就是过拟合。(These more complex models can lead to a phenomenon known as overfitting the data, which essentially means they follow the errors, or noise, too closely)
2.3.2 无参估计法
无参估计法来拟合𝑓(𝑥)就显得非常直接了,它不做任何关于𝑓(𝑥)的函数形式的预设(Non-parametric methods do not make explicit assumptions about the functional form of 𝑓),在避免过于“灵活”的前提下(为了避免过拟合),尽量用更丰富的函数形式去拟合蕴藏在训练数据里的𝑓(𝑥)。(They have the potential to accurately fit a wider range of possible shapes for 𝑓)
无参估计法就很好地弥补了有参估计的最大不足,即它不做任何函数形式的假设,也就不存在假设不准的问题了。但,任何方法都有不足的一面,无参估计最大的不足在于,它需要比有参估计法多得多的训练数据来完成对𝑓(𝑥)的拟合。(But non-parametric approaches do suffer from a major disadvantage: since they do not reduce the problem of estimating 𝑓 to a small number of parameters, a very large number of observations (far more than is typically needed for a parametric approach) is required in order to obtain an accurate estimate for 𝑓)
2.4 在模型解释性和预测精度之间如何权衡?
图3表示了在模型可解释性和复杂度的二维空间里,一些常用的机器学习模型所处的位置(里面提到的模型后续都会讲解到)。大家可能会问,既然有精度更高的模型,为啥那些“低端”模型还有生存空间呢?(why would we ever choose to use a more restrictive method instead of a very flexible approach?)原因就是,有的时候, 我们的研究重点在于探究变量与目标的内在联系(inference),而不仅仅是预测出来的那个目标数字(prediction)。(If we are mainly interested in inference, then restrictive models are much more interpretable)
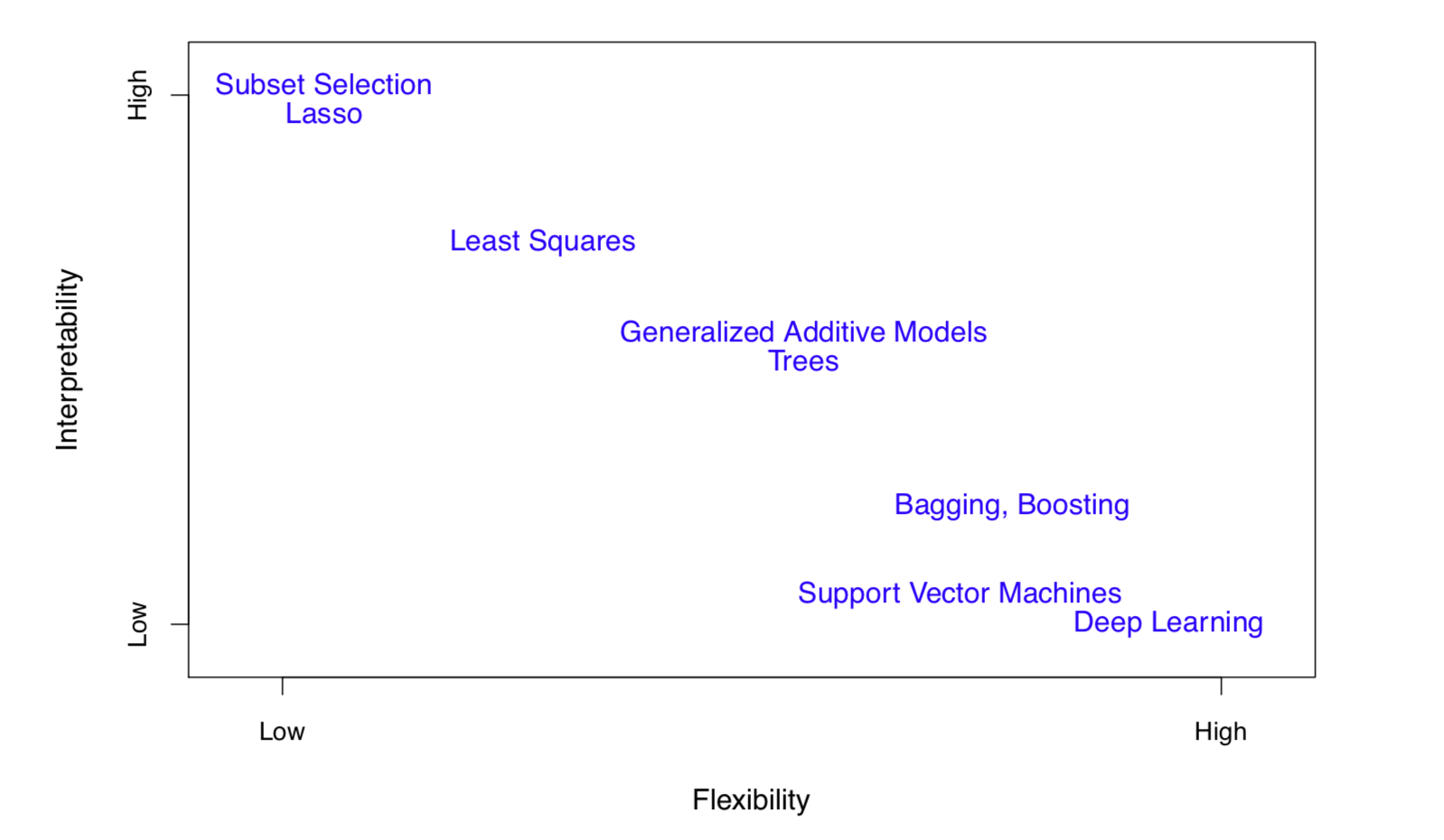
图 3:一些常用的机器学习模型在可解释性和复杂度的二维空间里的位置
2.5 如何区分监督学习和非监督学习?
绝大部分统计学习方法(也可以叫做机器学习方法)都会落到这两类:监督分类(Supervised)和非监督分类(Unsupervised)。(Most statistical learning problems fall into one of two categories: supervised or unsupervised)
简单来说,监督分类就是在准备拟合的训练数据中,既有自变量𝑋1,𝑋2,𝑋3…𝑋𝑝的值,也有因变量𝑦的值。在这种场景下,我们既可以做推论(inference),也可以做预测(prediction)。
而在非监督分类中,通常是没有因变量𝑦的值,只要自变量𝑋1,𝑋2,𝑋3…𝑋𝑝的值,我们也可以叫“非监督分类”为“聚类分析”(cluster analysis)。聚类分析看观测训练样本是否有“各自扎堆”的情况,如果这些样本能够自然地形成清晰的差异群体,那么我们有理由相信,这些群体之间必然存在显著的特征差异,而这些具有差异的特征,可能正是我们所需的。下图4就展示了一个简单的聚类分析的结果,左边的样本数据能很好的分出3类,但右边的样本数据中则存在不同类之间的重叠。如果变量比较少(比如图4中只有2个变量),则聚类分析可以通过做图(scatterplot)来完成,但一旦样本中的变量数过多(一般>=4),则通过作图的方式就难以完成聚类分析了。后面的章节会单独介绍常用的聚类分析方法。
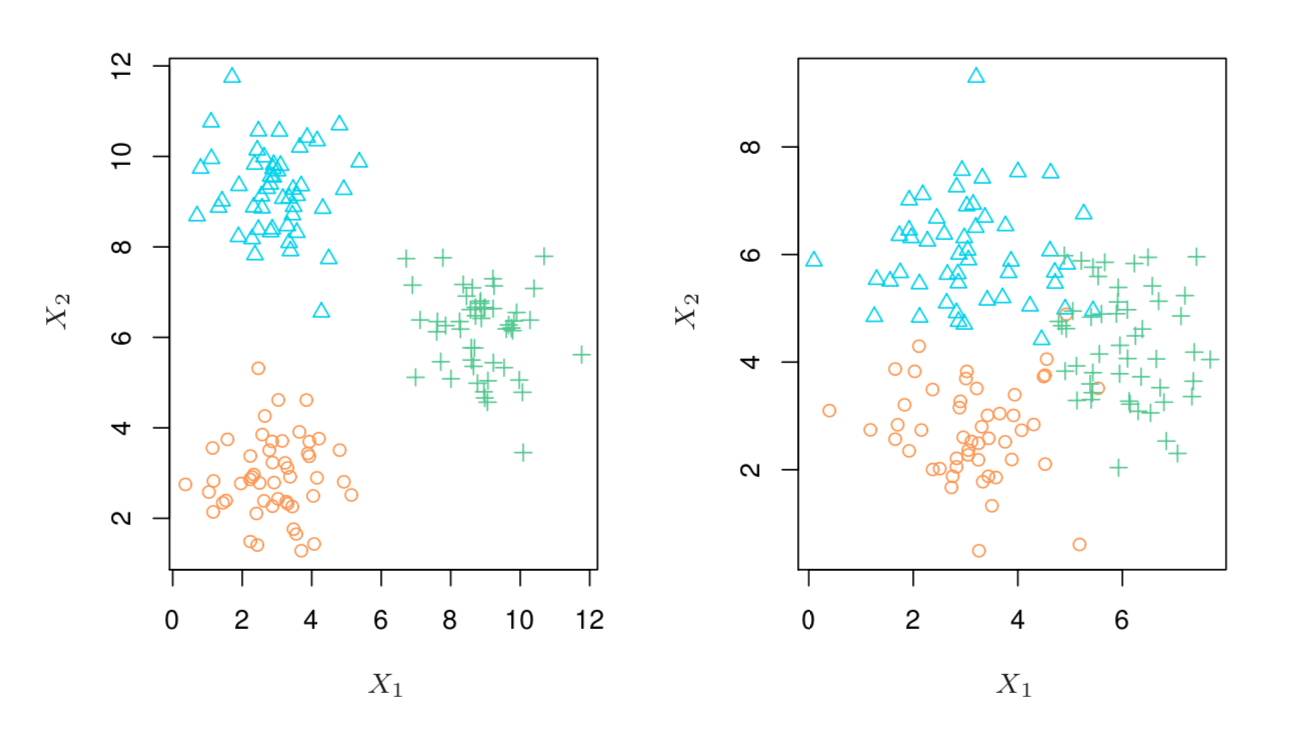
图 4:一些常用的机器学习模型在可解释性和复杂度的二维空间里的位置
2.6 如何区分回归问题和分类问题?
很简单,区分回归还是分类问题,就看自变量𝑦的值是连续性数值还是离散型。(We tend to refer to problems with a quantitative response as regression problems, while those involving a qualitative response are often referred to as classification problems)。比如预测一个人的工资或者一座房产的价值,就可以看做是回归模型,因为工资和房价都是连续的数字;相反,预测明天是下雨还是天晴,预测比赛胜还是负,则可以看做预测模型,因为天气情况和比赛结果是可枚举的离散值。当然,有些模型既可以看做是回归问题,也可以看做是分类问题,比如后面会讲到的逻辑回归(logistic regression)。因为从输出概率的角度讲,逻辑回归是回归模型,但从本身逻辑回归的用途来讲,它也是个分类模型。
2.6 如何去评估模型的质量?
2.6.1 回归问题
在回归问题中,我们最常用的衡量模型精度的指标是均方误差(the mean squared error (MSE)),计算公式如下:
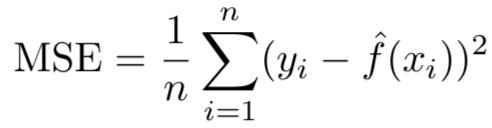
其中𝑓′(𝑥𝑖)表示我们用拟合的𝑓′(𝑥)去近似代替真实但未知的𝑓(𝑥),并将第𝑖个变量代入𝑓′(𝑥)得到的预测值。理论上,我们希望这个𝑓′(𝑥𝑖)值与真实的𝑦𝑖值相差越小越好。
这里的𝑀𝑆𝐸可以分为训练𝑀𝑆𝐸(train MSE),即用训练样本得到的𝑀𝑆𝐸,和测试𝑀𝑆𝐸(test MSE),即用测试样本得到的𝑀𝑆𝐸。相较于训练𝑀𝑆𝐸,我们更关心测试𝑀𝑆𝐸。(We are interested in the accuracy of the predictions that we obtain when we apply our method to previously unseen test data)
那我们怎么得到测试𝑀𝑆𝐸呢?如果样本总量很大的话,我们可以事先留出一部分数据作为测试数据(test data),然后将训练数据(train data)拟合得到的模型去测试数据上进行预测,就可以得到测试𝑀𝑆𝐸(test MSE)了。
2.6.2 分类问题
分类问题中,最直接的评价模型精度的方法就是错误率(error rate,错误分类的样本数/总样本数),计算公式如下:
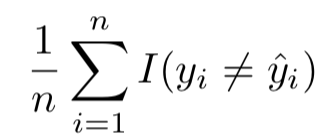
其中,𝐼(𝑦𝑖≠𝑦𝑖′)是指示函数(indicator function),如果𝑦𝑖≠𝑦𝑖′为真则返回为1,否则返回0。
跟回归问题一样,我们更关心在测试样本上,这个评估指标的大小。后面会介绍用于评价分类精度的更多更科学的指标。
如何能让这个测试错误率(the test error rate)变得最小呢?其实方法很简单,就是把样本分类到概率最高的那一类上去(assigns each observation to the most likely class, given its predictor values),也就是贝叶斯分类器的基本原理。
![]()
这是个条件概率,其中𝑗代表第𝑗个类别,表示某个具体的待分类的样本。贝叶斯分类器就是把
赋值给条件概率𝑃𝑟最高的那个第𝑗类。
下图5展示了在模拟数据上用贝叶斯分类器画出的决策边界(Bayes decision boundary),紫色虚线代表着概率刚好等于0.5(因为是模拟数据,所以作者能准确地计算出每个点代表的条件概率)。若样本落在了虚线的左侧,就分为橘色的类;若样本落在了虚线的右侧,就分为蓝色的类。这样分出的类,它的测试错误率(the test error rate)理论上是最低的。
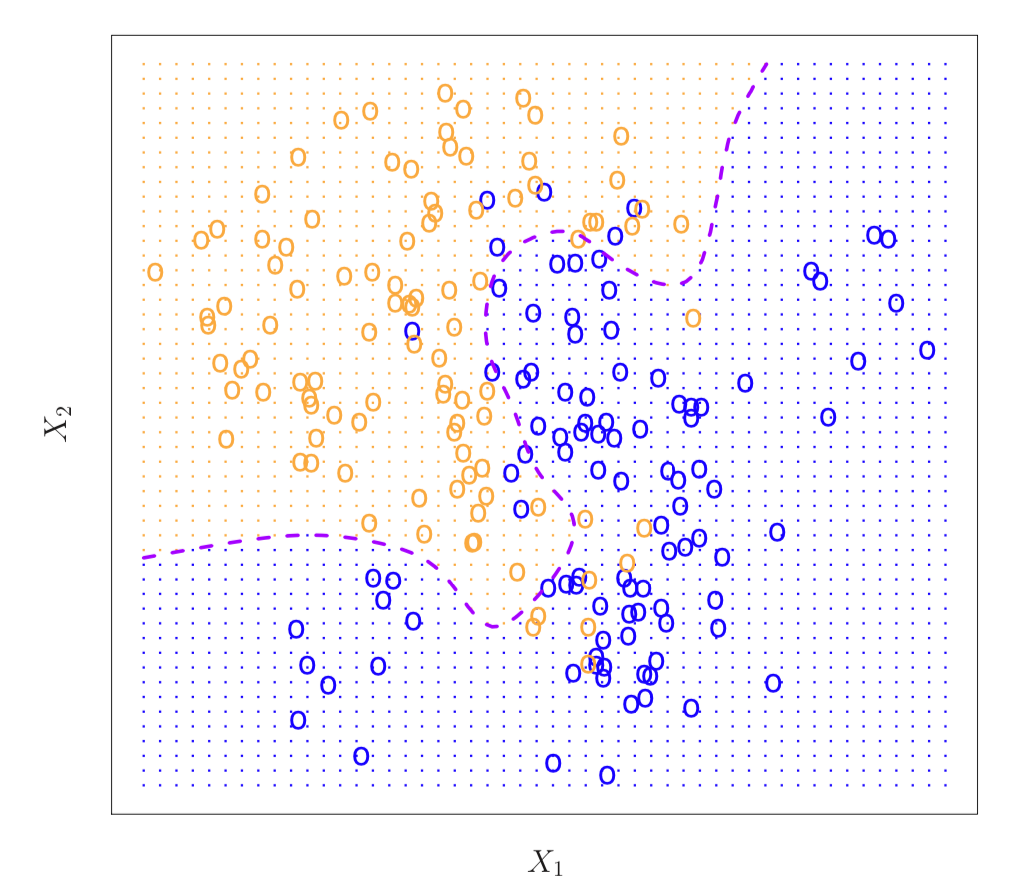
图 5:在模拟数据中,体现出的贝叶斯分类边界
理论上,我们都希望用贝叶斯分类器去处理分类问题。但现实中,我们是不可能知道数据背后隐藏的真实的概率分布的,所以并不能得到贝叶斯分类器。(In theory we would always like to predict qualitative responses using the Bayes classifier. But for real data, we do not know the conditional distribution of Y given X, and so computing the Bayes classifier is impossible)
虽然我们无法得到准确的概率函数,但我们可以去预估这个概率。在众多的预估方法中,𝐾𝑁𝑁就是其中一个方法。后续章节会讲解这个方法的算法和特性。(Many approaches attempt to estimate the conditional distribution of Y given X, and then classify a given observation to the class with highest estimated probability. One such method is the K-nearest neighbors (KNN) classifier)
下图展示了在相同的模拟数据中,𝐾𝑁𝑁分类器(k=10)的决策边界与贝叶斯分类器的决策边界的比较。可以看出,𝐾𝑁𝑁分类器很好地拟合了贝叶斯分类器。
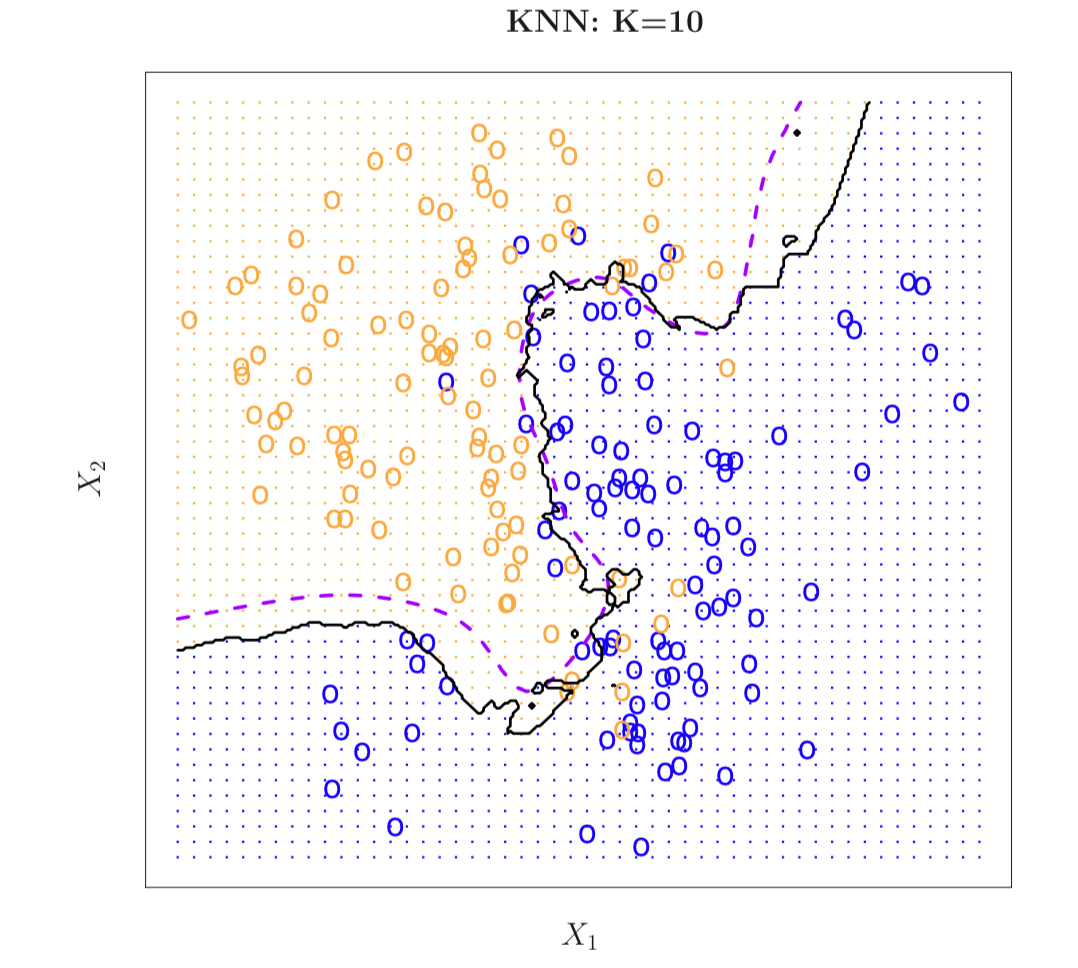
图 6:在模拟数据中,用KNN分类器的决策边界与贝叶斯分类器的决策边界的比较
2.7 在回归和分类情景下,偏差和方差如何进行权衡?
首先,以回归情景为例,下面这个公式很好地体现了我们日常所称的“预测的误差”到底包含那几部分:
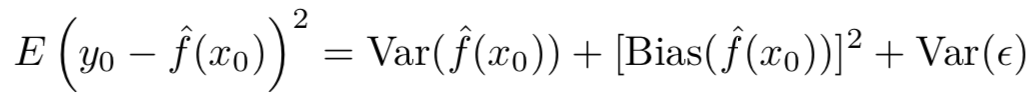
上面公式的推导过程书中没有详细展开,不过我们从结果中可以看出,“预测的误差”包含三个部分:𝑓′(𝑥0)的方差(variance),𝑓′(𝑥0)的偏差(bias)平方,以及随机误差项(random error)的方差(variance)。(Though the mathematical proof is beyond the scope of this book, it is possible to show that the expected test 𝑀𝑆𝐸, for a given value 𝑥0, can always be decomposed into the sum of three fundamental quantities: the variance of 𝑓′(𝑥0), the squared bias of 𝑓′(𝑥0) and the variance of the error terms 𝜀)
如何理解𝐸(𝑦0−𝑓′(𝑥0))平方表达的意思呢?简单来说,可以理解为,在很多训练数据集上,训练得到了很多个不同的𝑓′(𝑥),然后用这些𝑓′(𝑥)分别代入𝑥0做计算,得到了很多个𝑓′(𝑥0)的值,同时也就得到很多个(𝑦0−𝑓′(𝑥0))平方的值。最后,对得到的(𝑦0−𝑓′(𝑥0))平方的不同值求平均值。
那到底什么是偏差(bias)?什么是方差(variance)呢?(What do we mean by the variance and bias of a statistical learning method?)
- 偏差:在建模的时候,我们用了一个偏简单的模型去拟合一个偏复杂的场景(比如用线性模型去拟合非线性场景)所带来的误差,就叫偏差。这种由模型自身的局限性带来的误差,用再多的样本也无法被抹除。(Bias refers to the error that is introduced by approximating a real-life problem, which may be extremely complicated, by a much simpler model. The true 𝑓f is substantially non-linear, so no matter how many training observations we are given, it will not be possible to produce an accurate estimate using linear regression)
- 方差:在建模的时候,当用同一个大样本集下不同的子样本集去拟合模型时,得到的𝑓′f′的变化幅度,就叫方差。理论上,不同子样本集得到的𝑓′f′应该大同小异,所以方差不会很大;但如果选择的模型方法本身内在方差很大的话,稍微变动下某个子样本集里的数据,拟合出来的𝑓′f′变动就很大了。一般来说,越复杂的模型,其内在的方差越大。(Variance refers to the amount by which𝑓′f′would change if we estimated it using a different training data set. However, if a method has high variance then small changes in the training data can result in large changes in 𝑓′f′. In general, more flexible statistical methods have higher variance)
那什么又叫做偏差和方差的权衡呢?下面这段英文真的非常经典,一语道破精髓:This is referred to as a trade-off because it is easy to obtain a method with extremely low bias but high variance (for instance, by drawing a curve that passes through every single training observation) or a method with very low variance but high bias (by fitting a horizontal line to the data). The challenge lies in finding a method for which both the variance and the squared bias are low. 意思是,单纯得到一个方差极低的,或者一个偏差极低的模型非常容易。比如画一条水平线去拟合数据就能得到方差极低的模型;画一条穿过所有数据点的线去拟合数据就能得到偏差极低的模型。但,要兼顾两者都处于较低水平,这就是所谓的权衡了。
上面关于𝐸(𝑦0−𝑓′(𝑥0))平方的公式和下面的图,都是对偏差和方差权衡(The Bias-Variance Trade-Off)非常好的体现。
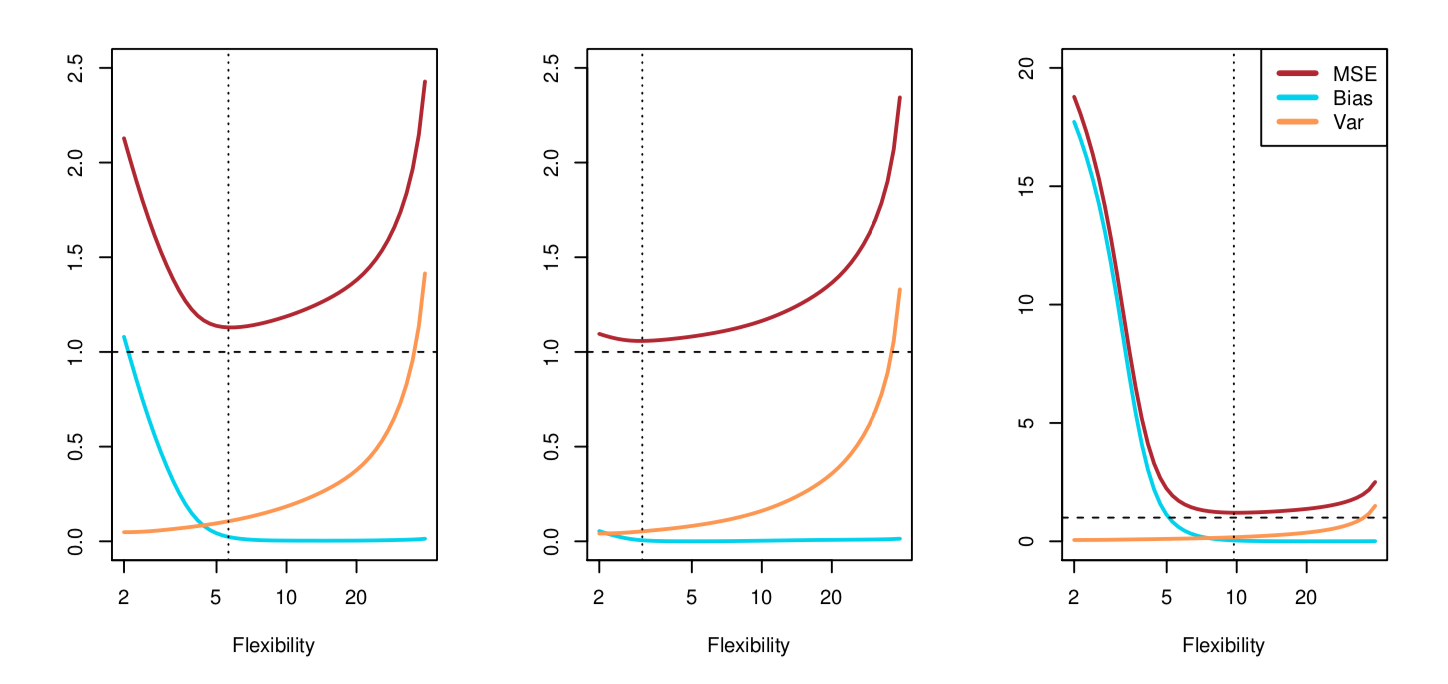
图 7:偏差、方差和MSE的关系,很好地诠释了trade-off
下图8 展示了模型的复杂度与测试𝑀𝑆𝐸的关系。左边的图里,展示了不同复杂度的模型对训练样本(空心圈)的拟合情况,其中黑色的实线表示真实的𝑓(𝑥),其他颜色的线表示拟合的𝑓′(𝑥)。黄色,蓝色,绿色三种颜色对应的曲线,复杂度依次升高(从图中就可以看出,曲线越来越“弯曲”,“灵活”)。右图中,灰色的线表示训练𝑀𝑆𝐸,可以看出,训练𝑀𝑆𝐸随着模型复杂度的增加而单调减小;红色的线表示测试𝑀𝑆𝐸,可以看出,测试𝑀𝑆𝐸随着模型复杂度的增加呈现先减小后增加的𝑈型特征(U-shape)。
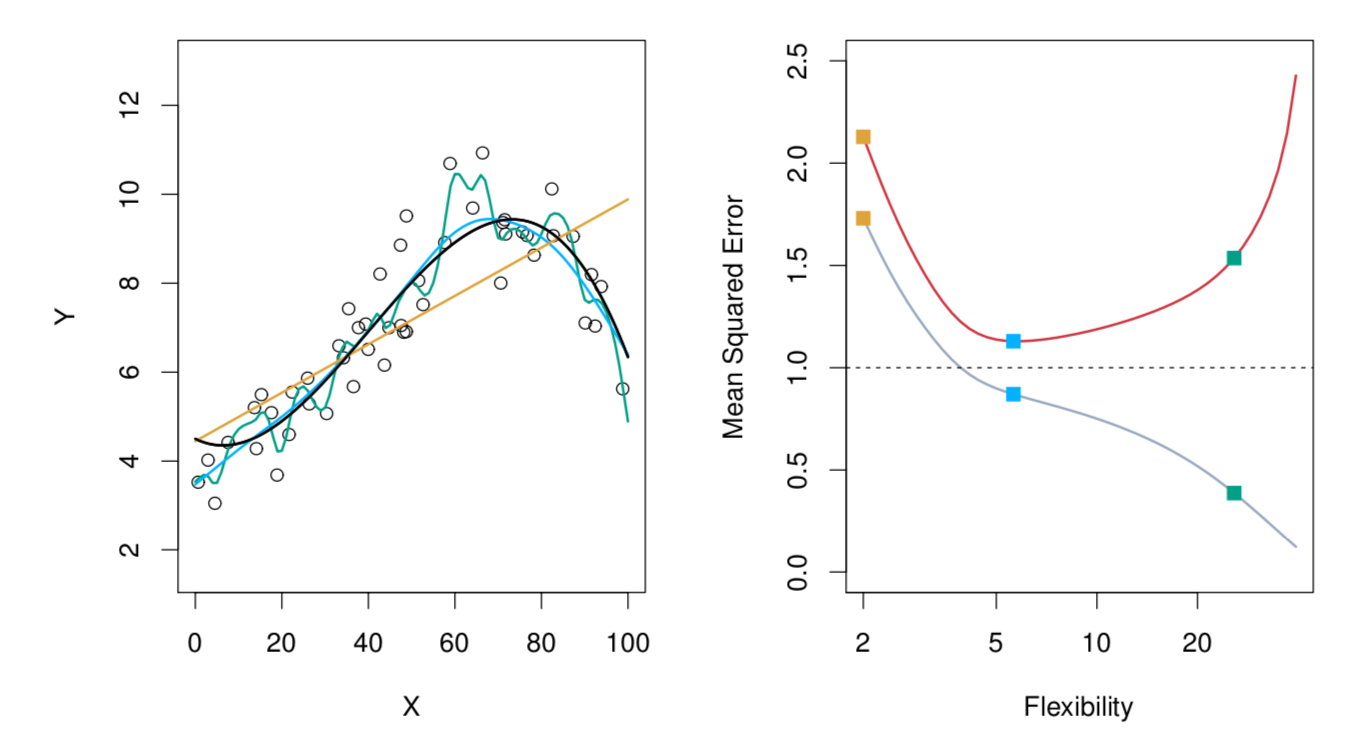
图8:模型的复杂度与测试MSE的关系
3. 引用























 770
770

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








