豆瓣9.6分统计学神作ISL之第六章读书笔记（下），带你系统学习主成分分析与回归、偏最小二乘法回归以及对高维数据的思考

1.原文内容概要

鉴于第六章内容的丰富性，读书笔记分为了【上】、【下】两篇，以细致解读其内涵。

在【上】篇里，我们已经深入探讨了变量筛选（Subset Selection）和正则化技术（Shrinkage or Regularization），这两种强大的工具帮助我们锁定关键因素，简化模型结构，有效预防了过拟合的陷阱。

在【下】篇中，我们将解锁数据分析的另一项强大武器——降维。想象一下，将复杂的数据迷宫简化为一张清晰的地图，这正是降维的魅力所在。它不仅能够帮我们剔除冗余的信息，还能让我们在低维度的空间中洞察数据的本质，从而更快地找到解决问题的钥匙。

在这个章节中，我们不仅仅是学习一种技术，而是在掌握如何将复杂问题简化的艺术，就如同将一幅抽象画转化为线条明朗、意蕴深远的素描。

2.算法知识总结

2.1 降维方法（Dimension Reduction Methods）

在之前关于模型简化的探讨中，主要关注了两种策略来控制模型的复杂度：
1）筛选性拟合，即从众多变量中甄选出最具影响力的子集；
2）系数衰减，即通过减少变量权重至微乎其微趋向于零或等于零。

这两种方法有一个共同特点，即自始至终都是拟合的原始变量（All of these methods are defined using the original predictors, $X_1,X_2,...,X_p$）。

在本章中，我们将探索一种与既往方法迥异的策略——降维。这种方法不满足于对原始变量的简单筛选或权重调整，而是先行一步，将原始变量进行一番巧妙的转换。随后，使用这些经过转换的新变量来构建模型（例如线性模型），并实施拟合（例如最小二乘法）。
（We now explore a class of approaches that transform the predictors and then fit a least squares model using the transformed variables. We will refer to these techniques as dimension reduction methods）

我们设$Z_1,Z_2,\dots ,Z_M$为原始$p$个变量经过线性组合后得到的$M$个新变量，其中$M<p$，其数学公式如下：

其中${\Phi }_{1m},{\Phi }_{2m}...,{\Phi }_{pm}$是常数项，$m=1,...,M$。再用$Z_1,Z_2,\dots ,Z_M$作为自变量代入线性模型，最终拟合的模型表达式就变成了：

所有降维法都分两步：首先，通过特定方法获得转换后的变量；接着，利用这些新变量进行模型拟合。其中核心在于转换方式的选定，在实际应用中，主成分分析（principal components）和偏最小二乘法（partial least squares）是两种常用的降维手段。（All dimension reduction methods work in two steps. First, the transformed predictors $Z_1,Z_2,...,Z_M$are obtained. Second, the model is fit using these $M$_ _predictors）

2.1.1 主成分回归（Principal Components Regression）

主成分分析（Principal Components Analysis，简称PCA）是一种很常用的降维技术，它的细节将在第12章“非监督分类探索”的读书笔记中深入剖析。在本章中，我们将重点探讨其作为回归分析中降维工具的巧妙应用（即主成分回归），揭示如何利用PCA将复杂数据简化，以洞察隐藏在数据深层的结构。

2.1.1.1 主成分分析概述

PCA是一种降维技术，其核心在于将高维数据（$n\times p$）映射到低维空间（$n\times m$），其中$m$小于$p$（注意，这里的样本量$n$是没变的哟）。通过这种变换，PCA旨在找到最能代表数据变异性（variability）的方向，即第一主成分（The first principal component direction of the data is that along which the observations vary the most）。具体而言，第一主成分是这样一个方向：样本点在该方向上的投影（project）能最大化它们之间的方差，意味着在这个方向上，样本点的分布最为分散，从而有效揭示不同样本之间的差异）。所谓投影，就是指将样本点映射到主成分方向上，以找到该方向上距离每个样本点最近的点（Projecting a point onto a line simply involves finding the location on the line which is closest to the point）。

在下图中，作者运用了一个模拟的广告数据集作为演示案例。该数据集包含两个主要变量：100个城市的人口数量（Population）和这些城市在广告上的投入（Ad Spending）。图中以紫色点表示原始的数据样本，而绿色的线条则指示了第一主成分的方向。虚线的小线段描绘了数据点向这一主成分方向投射的过程，该过程基于寻找最小距离的原则。投射后的点则以小叉点表示，它们清晰地展示了数据在主成分方向上的分布情况。

图形化展示提供了直观性，但如何用数学公式来表达投射第一主成分方向的过程呢？公式如下所示：


其中${\Phi }_{11}=0.839$，${\Phi }_{21}=0.544$，它们的官方名字叫主成分载荷（principal component loadings），它们是原始变量$i$在主成分$j$上的权重，反映了原始变量对主成分的贡献程度；$\overline{pop}$表示人口数（$pop$）这个变量的平均值，$\overline{ad}$同理，它们是描述数据集的中心趋势或位置统计量。

上面的$Z_1$是第一主成分的向量表达形式，其中向量里面包含的具体值，$z_{11},...,z_{n1}$，也有个官方名字，叫做主成分分数（principal component scores），计算公式可表示为：


在这个例子中，主成分载荷（${\Phi }_{11}$和${\Phi }_{21}$**）是怎么确定的呢？**其实它们的内在含义是，在${\Phi }_{11}^2+{\Phi }_{21}^2=1$这个条件下，寻找到一对组合值，使得这个组合能使下面的方差值最大化。


将上面的图经过旋转调整，使第一主成分与$x$轴平行，从而更直观地展示了其对应的取值。从新的图形中可以清晰地看到位于左下角的点，其第一主成分分数为$-26.1$。这个负数分数意味着这个城市的人口数量和广告投入都很有可能低于这100个城市的平均水平。

当获得了第一主成分后，进一步探究它与原始变量——即人口数量和广告投入——之间的相关性是非常重要的。如下图所示，第一主成分与人口数量和广告投入这两个原始变量呈现出显著的相关关系，这有力地证明了第一主成分成功地捕获了这两个变量各自的主要信息。这种高度的相关性表明，通过主成分分析，我们能够将复杂的数据集简化为一个单一的维度，同时保留了原始数据中的关键信息。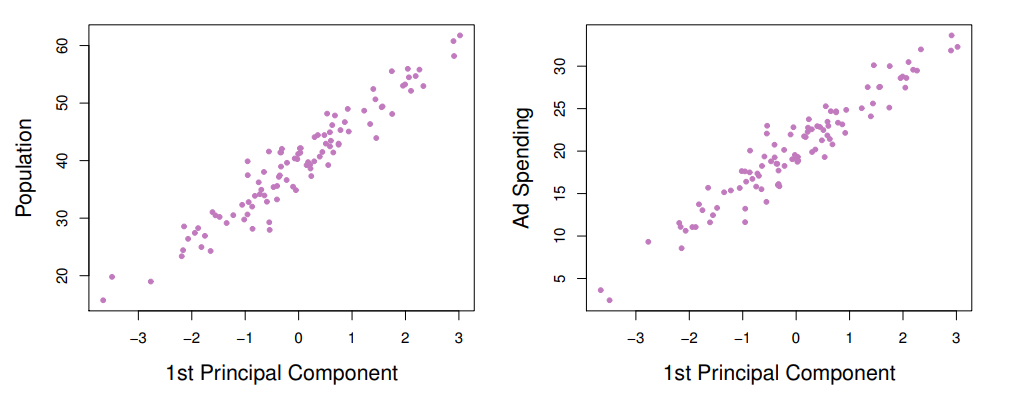

确定了第一主成分之后，我们便好奇第二主成分、第三主成分等。通常情况下，模型中原始变量的数量决定了主成分的总数。在本例中，由于原始变量有两个——人口数和广告投入，因此主成分的总数也是两个。在第一主成分的基础上，构建第二主成分的限制条件如下所示：
1）它与第一主成分必须完全不相关，确保两个主成分之间不存在信息重叠；
2）在满足这一条件的基础上，第二主成分应使方差最大化，以捕捉数据中尽可能多的独特信息。

在只有两个变量的场景中（即本案例），第二主成分的方向实际上是与第一主成分方向垂直的那个方向。通过简单的线性代数计算（后续我也会分享MIT线性代数教材读书笔记），即可得到第二主成分的主成分载荷，如下所示：

但从下面第二主成分与原始变量的散点图可知，这个第二主成分跟这俩变量几乎没有关系，意味着它几乎没包含原始变量任何有效的信息，故可舍弃之。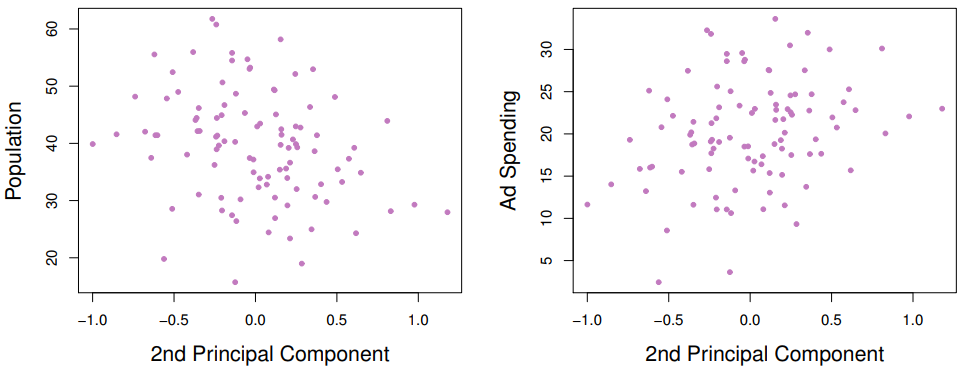

2.1.1.2 主成分回归

主成分回归（PCR）是在完成主成分分析（PCA）之后的一种分析方法，其中将PCA得到的新变量（即各原始变量对应的主成分分数）作为自变量代入线性回归模型中进行拟合。（The principal components regression (PCR) approach involves constructing the first $M$ principal components, $Z_1,...,Z_M$, and then using these components as the predictors in a linear regression model that is fit using least squares）

我们通常假设，那些使自变量（$X$）差异最大化的方向也与因变量（$Y$）具有较强的相关性（We assume that the directions in which $X_1,...,X_p$ show the most variation are the directions that are associated with $Y$）。当然，上述假设并非绝对准确，但在实际应用中，根据本书作者的经验，这一假设往往能够近似成立（While this assumption is not guaranteed to be true, it often turns out to be a reasonable enough approximation to give good results）。

PCR相较于普通线性回归的优势在于其能够缓解过拟合的情况。如下图所示，PCR方式拟合的模型在测试集上的误差已经非常接近极限最小值了（irreducible error Var($\epsilon$)），也就是水平虚线的位置。

一般而言，当只有少数几个自变量与因变量之间存在显著的线性关系时，PCR的效果才会更佳（PCR will tend to do well in cases when the first few principal components are sufficient to capture most of the variation in the predictors as well as the relationship with the response）。至于到底需要多少个主成分，我们通常用交叉验证的方法来确定，如下图所示：

需要特别注意的是，在执行PCR分析前，需要先对各个变量进行标准化处理，这通常是通过将每个变量减去其均值，再除以其标准差来完成的，以确保所有变量都在同一尺度上。这样做有助于消除不同量纲和变量尺度的影响，使得分析结果更为准确和可靠。

2.1.2 偏最小二乘法回归（Partial Least Squares Regression）

我们之前提到的一个关于PCR的局限是，它确定的主成分方向虽然能最大程度上解释自变量的方差，但这个方向并不保证同样能最大程度地解释因变量的方差（PCR suffers from a drawback: there is no guarantee that the directions that best explain the predictors will also be the best directions to use for predicting the response）。原因在于PCR在确定这些主成分时仅考虑了自变量之间的关系，而没有将因变量的信息纳入考虑，这是一种无监督的方法。

为了解决这个问题，偏最小二乘法（PLS）便应运而生，它是一种有监督的方法（a supervised** **alternative）。简单来说，它能够在考虑自变量之间关系的同时，也兼顾因变量的信息，从而找到既能解释自变量也能解释因变量变异的最佳组合（Roughly speaking, the PLS approach attempts to find directions that help explain both the response and the predictors）。

在偏最小二乘法（PLS）中，第一主成分的提取和拟合过程可以概括为以下步骤：

1. 首先，对所有的自变量进行标准化处理，以确保它们在同一尺度上并消除量纲的影响。
2. 然后，分别针对每个自变量和因变量进行一元线性回归分析，将得到的回归系数作为主成分载荷（${\Phi }_{1m},{\Phi }_{2m},...,{\Phi }_{pm}$），这些载荷反映了各个自变量与因变量之间的关系强度。
3. 接下来，利用主成分分析（PCA）的方法，结合上一步骤得到的主成分载荷，计算出第一主成分$Z_1$。这一步骤涉及自变量的线性组合，旨在提取最大的变异信息。

通过以上步骤，PLS能够确保第一主成分不仅解释了自变量空间的最大方差，而且与因变量保持了相关性。

有了第一主成分后，就可以进行第二主成分的提取，过程通常包括以下步骤：

1. 首先，针对每个原始自变量与第一主成分$Z_1$进行一元线性回归分析。在此过程中，我们计算得到回归模型的残差，这些残差代表了第一主成分未能解释的自变量信息（These residuals can be interpreted as the remaining information that has not been explained by the first PLS direction），并且它们与$Z_1$正交，即在统计意义上相互独立。
2. 然后，使用上一步骤中获得的残差作为新的自变量集合，构建主成分载荷。由于这些残差与$Z_1$正交，因此它们反映了与第一主成分不相关的数据结构。
3. 接着，采取与提取第一主成分$Z_1$相同的方法，利用新的主成分载荷计算出第二主成分$Z_2$。这一步同样涉及数据的线性组合，以捕捉原始数据中剩余的变异信息。

通过这个过程，第二主成分$Z_2$不仅补充了第一主成分$Z_1$未能覆盖的信息，而且确保了与$Z_1$在统计上的独立性。这样的逐步提取方法使得PLS能够有效地从原始自变量中分离出与因变量相关的关键信息，并构建出一个既考虑了预测性能又具有较低维度的数据表示。

之后可以用相同的逻辑继续提取第三、第四……第n个主成分。

尽管PLS在理论上兼顾了自变量与因变量的关系，但实际应用中的效果并不总是优于PCR（In practice it often performs no better than ridge regression or PCR）。这主要是因为PLS和PCR各自适用于不同条件和不同类型的数据。例如，当自变量之间的多重共线性不是很严重或者样本量足够大时，PCR可能会表现得更好，因为它完全基于自变量的内部结构进行维度缩减，而不考虑因变量。反之，PLS通过同时考虑自变量和因变量来寻找相关的成分，所以它在自变量存在高度共线性或者样本量较小的情况下通常表现更佳。然而，如果因变量的信息并没有增加有用的预测能力，或者模型过度拟合了噪声，PLS的实际预测性能可能不如PCR（While the supervised dimension reduction of PLS can reduce bias, it also has the potential to increase variance, so that the overall benefit of PLS relative to PCR is a wash）。

因此，在选择PLS或PCR作为回归分析工具时，应当根据具体的数据特性、问题背景以及模型的预测目标来综合判断。

2.2 高维空间的思考（Considerations in High Dimensions）

2.2.1 高维数据的定义

高维数据的定义并不仅仅依赖于自变量的绝对数量，而是基于自变量的数量与样本数量的相对关系来确定。如果样本数量远大于自变量的数量，即使自变量的绝对数量很大，这种情况也不被视为高维数据（We have defined the high-dimensional setting as the case where the number of features p is larger than the number of observations n）。

2.2.2 高维灾难（curse of dimensionality）

本书作者用最小二乘法回归来举例。在高维数据环境中，最小二乘法回归可能会遇到系数解的不稳定性问题。当自变量的数量接近或超过样本数量时，最小二乘法通常能够找到一个完美拟合样本数据的系数解。然而，这种解往往是过拟合的，因为它可能捕捉到了样本中的随机噪声，而不是自变量与因变量之间真实的关系。

假如只有一个变量$X$，甲数据集有20个样本（因此甲是低维数据），乙数据集只有2个样本（因此乙是高维数据）。如下图所示，在乙数据集中，最小二乘法明显是过拟合了，而在甲数据集里则不会出现这个情况。

作者又模拟了另外一个数据集，数据集里有20个样本，样本中的自变量也有20个，但都与因变量毫无关系。神奇的是，用这些毫不相关的预测变量对因变量进行拟合，得到的模型$R^2$（决策系数）、训练误差竟然随着模型中自变量数量的增加而优化到了极致（下面的左图和中间的图所示），这就是高维数据的假象。但这个假象还是被测试误差所戳破了（下面的右图）。这个例子中，测试误差揭示了高维数据假象背后的真相：模型并没有真正捕捉到自变量与因变量之间的关系，而是简单地拟合了训练数据中的随机波动。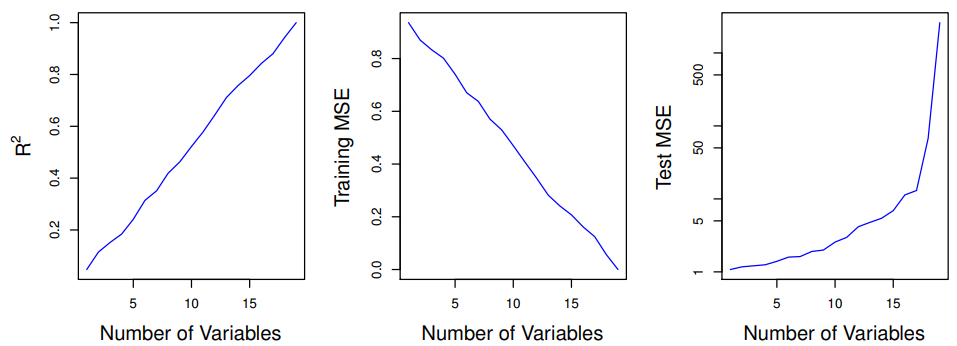

另外，还有一个点需要提醒，在高维数据中，由于变量的数量很多，变量之间出现多重共线性的问题几乎是不可避免的。这种情况下，使用第六章（上）读书笔记中提到的变量筛选方法来确定“重要”的变量时，选出的“最佳组合”并非真是全场最佳，这意味着可能存在其他的变量组合，它们对于预测因变量来说同样有效，甚至更有效。所以，在拟合高维数据时，不要轻易相信变量筛选算法选出的所谓的重要变量，我们一定记住，测试集上的表现才是最真实的（But we must be careful not to overstate the results obtained, and to make it clear that what we have identified is simply one of many possible models_ _for predicting response, and that it must be further validated on independent data sets ）。

引用