eLife：EEG和MEG中相位数据的贝叶斯分析

摘要：脑电图（EEG）和脑磁图（MEG）记录是研究人类神经反应的宝贵工具，但它们存在噪音，并可能受到多种过程的影响。为了解决这一问题，一个有效的方法是使用特定频率的刺激，并测量响应相位的一致性。本文描述了一种测量相位一致性的贝叶斯方法，并使用神经语言学的示例和模拟数据进行了阐述。本研究建议，与传统的统计方法相比，贝叶斯方法更具描述性和可解释性，并且在检测与刺激相关的差异时对参与者数量要求更低。

在脑电图（EEG）或脑磁图（MEG）频率标记实验中，刺激以特定频率呈现，神经反应也在该频率下进行量化。这比典型的事件相关电位（ERP）范式提供了更强大的响应，因为大脑对刺激的反应发生在预定义的刺激频率上，而来自其他频率的噪音不会污染感兴趣的反应。通常通过计算试验间相位一致性（ITPC）来进行这种量化。然而，贝叶斯估计方法可以更好地来实现量化。相比ITPC，它可以保留更多的信息。为了证明这一点，本研究通过将这两种方法应用于两个不同的频率标记实验数据集，并使用模拟数据进行比较。

相位一致性是对波（例如脑波）的测量，用于量化它们在固定频率下振荡行为的相似程度。换句话说，虽然波每分钟振荡的次数可能相同，但相对于彼此的波的相对时序可能是不同的（不一致）或相似的（一致）。在神经科学中，科学家研究脑波的相位一致性，以了解大脑对外部刺激的反应，例如在实验中它们是否以固定频率出现。为了做到这一点，通常使用一种称为“试验间相位一致性”（ITPC）的统计量来量化相位一致性。当ITPC等于1时，波是完全一致的，即两个波之间没有偏移，波峰和波谷恰好同时出现。当ITPC等于0时，波是以完全随机的方式相互偏移的。相位一致性也可以建立在相位角度上，描述了每个波相对于零参考角度的偏移，以及包裹分布。包裹分布是相位角度的概率分布，表达了它们的相对可能性。包裹分布具有统计特性，包括均值和方差。包裹分布的方差可用于建模相位一致性，因为它明确表示了相位角度相对于均值的相似性：较大的方差意味着较小的一致性。

然ITPC是分析相位一致性的常用方法，但它是所谓的“汇总统计量”。使用ITPC进行分析会丢弃试验间数据中的有用信息，而使用相位角度可能不会丢失这些信息。因此，Dimmock、O’Donnell和Houghton着手确定是否可以创建一个直接基于相位角度（而不是ITPC）的相位一致性模型，并且比现有方法产生更好的结果。Dimmock、O’Donnell和Houghton使用实验数据和模拟数据将他们的模型与ITPC进行比较。比较表明，他们的模型可以在比ITPC更小的样本量下检测大脑对语法短语的同步，且假阳性较少。传统的研究大脑语言加工的工具通常会在数据中产生大量噪音，这使得分析测量变得困难。Dimmock、O’Donnell和Houghton证明了大脑不仅仅是对短语中的“惊喜因素”做出反应，正如一些人所认为的那样，而且还对它们的语法类别做出反应。这项研究表明，使用基于相位角度的模型可以比常用的ITPC方法更好地分析相位一致性。这对研究大脑语言加工的科研人员尤其有益，因为传统工具通常产生嘈杂的数据。通过将这种模型与其他方法结合使用，研究人员可以对他们的结果获得不同的视角，并可能在数据中识别新特征。这在样本量较小的研究中尤为有益。

频率标记是视觉研究中一个成熟的工具，通常被称为稳态视觉诱发电位。最初，它主要用于研究低级加工和注意力，但后来也被用于更复杂的认知任务，如面部识别和辨别、数字感知以及舞蹈动作的“人类特质”等。此外，频率标记还可以用于评估自闭症和精神分裂症等疾病，甚至用于研究神经对社交互动的反应。除了脑电图和脑磁图，相位一致性还被提议作为信号路由、组装形成和编码的机制。因此，相位一致性的测量对于理解大脑对外部刺激的响应至关重要。通常情况下，相位一致性通常用一种称为“试次间相位一致性”（ITPC）的统计量来量化。当ITPC等于1时，波完全一致，即两个波之间没有偏移，波峰和波谷完全同时出现。当ITPC等于0时，波之间的偏移是完全随机的。ITPC存在一些缺点。最明显的问题是，在ITPC的统计分析中，项目是参与者，而不是试验。是一个总结统计量，是方差的循环版本，因此它隐藏了两个阶段分析中的个体项目。然而，这很难比较参与者或电极之间的项目。

图1. 总结了不同条件下的试验间相位相干性（ITPC）。(A)彩色线显示了每个参与者在电极上平均后的ITPC，并在所有频率上进行追踪。通过对所有参与者轨迹的平均计算出的平均轨迹，用黑色覆盖。竖线分别将句子、短语和音节的频率标记为不断增加的频率。(B)采用未校正的配对双侧Wilcoxon符号秩检验（∗0.05，∗∗0.05，∗∗0.01）。(C) 每个条件对的ITPC差异在短语组频率上计算，并在整个颅骨上进行插值。

因此，本研究提出了一种贝叶斯方法来处理相位数据。贝叶斯方法提供了一个以模型及其结果为基础的叙述，描述了一个假设模型并量化其证据。贝叶斯方法从数据的参数化概率模型开始，提出了在给定一组模型参数的情况下数据的分布（似然）。完整的贝叶斯模型还包括参数的先验分布，旨在计算后验分布，即给定实验数据的参数的概率分布。这种计算遵循贝叶斯定理，其中似然代表了在给定一些参数的情况下数据的分布。与频率学方法相比，贝叶斯描述在许多方面更直观且更易于理解。

材料和方法

数据

本文考虑了两个实验数据集和模拟数据。第一个实验数据集是上文描述的短语数据；为了展示方法的普适性，我们还考虑了模拟数据。另一个数据集用于测量人工语言的统计学习。这些数据在此简要描述。我们使用贝叶斯模型分析了一项有趣的频率标记实验中的数据，该实验调查了人工语言任务中的统计学习。在这个实验中，18个音节被排列成六个三音节的单词，并以流的形式播放，使得伪词内部的转换概率为1，而伪词的最后一个音节与另一个音节的转换概率为0.2。其目标是评估伪词学习的程度。使用了频率标记范式。音节以恒定速率f呈现，使得三音节伪词的频率为f/3。统计学习的证据可以通过在这个频率及其谐波上使用ITPC来量化。在实验中，音节以4赫兹的频率呈现，导致三音节伪词的频率为1.33赫兹。每位参与者分别接受了基线（BL）和实验（EXP）两种条件。对于EXP条件，有六个伪词，其单词间的转换概率为0.2。BL条件包含与EXP相同的18个音节，但采用了不同的转换概率规则以消除规律性。在这项研究中，使用64个电极对40名成年参与者（25名女性，35名右撇子，年龄20-38岁）进行了三个44次试验的记录；其中39名参与者的脑电图记录完整，可用于分析。在“结果”部分，我们重述了这些数据的原始ITPC分析，并考虑了一个贝叶斯模型。

方法介绍

环形分布。在这种情况下，数据是一组相位，因此数据的模型是圆上的概率分布。ITPC的假设是相位在圆周上具有单峰分布，因此模型应该是圆上的单峰分布（见图5）。圆上的一类常见分布是由具有概率密度函数的包裹分布给出的。

图2. 模型构建和几何形状。(A) 不同比例参数值的包裹柯西密度函数示例。(B) Bundt分布的形状让人联想起在Bundt锡制作的蛋糕。(C) 平均相位是从具有对半径施加软约束的轴对称先验分布中抽样的。突出显示的点(x, y)给出了示例点的位置；这些点对应于使用angle(x, y)对包裹柯西分布进行抽样的平均角度。(D) S = 1 − R的示例分布决定了包裹柯西分布中的γ参数。S与其他参数（如条件和参与者编号）相关，通过逻辑回归，如方程19所示，回归中的斜率先验用于生成此处显示的分布；与以前一样，选择了两个示例点，每个点将对应于相应的包裹柯西分布中的不同γ值。(E) 绘制了包裹柯西分布的示例。

先验分布。选择包裹分布均值（μ）和决定分布离散度的γ的先验分布的很重要。μ的先验应在单位圆上是均匀的，对于每个参与者、条件和电极，都需要不同的μ值。然而，论文指出，理想的分布是在圆上均匀分布，而不是在区间上，这是由于拓扑结构不同。这一区别在使用MCMC方法进行抽样时至关重要，因为抽样器需要有效地探索参数空间。在MCMC抽样器中实现圆形先验的一种实用方法即在角坐标上均匀，在径向上限制抽样的二维分布。这种方法有助于避免从圆形先验分布中进行抽样的困难。Bundt分布是一个二维分布，其概率密度函数类似于Bundt蛋糕模具，用于制作（见图2B）。Bundt分布的径向轮廓并不重要，其目的是将样本限制在一个环上。该分布的均值为1，标准差为0.1，在图2C中呈现出可能的（x，y）值的金色环。实际上，模型中并未使用径向值，而是使用角度μ。Bundt分布的目的是避免从圆形先验分布进行抽样的困难。包裹柯西分布的量化线性模型为使用一个链接函数，首先从γ转换为循环方差S：γpce =−log（1−Spce），S pce = σ(υpce) 。S代表圆形方差，它的取值范围在0到1之间。为了将S限制在这个范围内，使用了一个称为logistic function的链接函数σ(υ)。在这里，υpce代表参与者、条件和电极对响应的影响。在这个模型中，υpce的计算是线性的，由αc、βpc和δce三部分组成。υpce = αc + βpc + δce表达了参与者、条件和电极对响应的综合影响。在模型中，这些量是线性的，是我们的主要关注对象。我们通过对这些量的后验分布进行抽样来计算结果。当然，这些量也需要先验。βpc的先验具有分层结构，允许在条件之间进行相关性分析；βpc模拟了参与者的响应：粗略地说，一个在某个条件下不专心的参与者可能在所有条件下都不专心。参与者的斜率βpc被分配了一个多元t-分布。这种多元参数化允许由于在条件内部和跨条件之间共享信息而进行同时的双向正则化过程。

结果

与ITPC结果比较：图3重新呈现了我们的分析结果，对比了图1中的ITPC分析。图3显示了使用RStan中的optimize函数估计的所有频率下的平均结果长度的点估计；与之前的图一样，在1.5626 Hz的频率下，AN条件显示出相位峰值，而其他条件没有。图3B则代表了尝试以尽可能接近实验结果中常用的“显著性差异括号”的方式呈现贝叶斯分析结果。在图3B的底部，我们可以看到每个条件下的平均结果长度的后验分布。这些后验分布是通过对描述条件对响应的影响的参数αc的后验样本进行转换得到的。结果表明，只有在形容词-名词（AN）条件下，大脑才会对短语刺激频率做出神经反应，而其他条件下则没有。这表明，大脑对AN条件下特定类型的短语做出了神经反应，而不是对所有短语都有反应。在图3C中，作者进行了电极对电极的比较，这些图表显示了比图1C中对相位相干性的分析更清晰的结构。需要注意的是，边缘后验概率不包含零的电极。此外，与图2C中的相位相干性分析不同，图3C中的后验概率远不止是一个点估计。

图3展示了参与者的专注度和局部电极效应。其中，图7A展示了AN条件下参与者效应的50/90%最高密度区间（HDIs）和后验中位数。图3B展示了每个条件下参与者斜率标准差的后验分布。图3C展示了从图6C中提取的头骨图，显示了AN-AV差异的后验分布。图7D展示了在头骨图上显示的位置上，当语法条件显示出更高的相位相干性时，电极差异的后验分布。

图3. 后验分布。(A)这些轨迹显示了使用优化程序计算出的所有58个频率的平均合成长度的点估计值。(B)每个转换条件效应αc的边际后验分布用小提琴图表示。条件差异的后期条件直接在上面给出，其颜色代表了进行比较的条件。例如，形容词-动词（AV）条件上方的绿色区间描述了后验差值AN−AV。后差差异和边缘区间均以90%最高密度区间（hdi）以后中位数表示。(C)后验中位数在颅骨上进行插值，用于所有条件下的比较。实验结果表示AN条件显示出左侧颞叶和右侧顶叶的响应，而其他条件没有。

个体效应

图4中绘制了参与者斜率βpc的90％最高密度区间（HDI），其中c = AN；β值越正，表示参与者的注意力越低，β值越负，表示参与者的注意力越高。从实验的角度来看，参与者的表现没有系统趋势，随着实验的进行而变得更好或更差。依赖于条件的参与者反应标准差的后验分布在图4B中绘制，似乎表明在具有结构但复杂或混乱的MP和ML条件中，参与者的反应存在更多跨参与者的变化，而在高度结构化和语法化的AN条件或几乎没有短语级别结构的RV和RR条件中，参与者的反应变化较小。

图4. 展示了参与者的专注度和局部电极效应。在图A中，作者绘制了形容词-名词（AN）条件下参与者效应的50/90%最高密度区间（HDIs）和后验中位数。在图B中，展示了每个条件下参与者斜率标准差的后验分布。图7C展示了从Figure 6C中提取的头骨图，显示了AN-AV差异的后验分布。图D展示了在头骨图上显示的位置上，当语法条件显示出更高的相位相干性时，电极差异的后验分布。

电极效应

该研究发现了电极依赖的反应模式，即P4和T7电极对AN条件的反应强于AV条件。通过使用模拟数据验证，研究表明在电极效应没有实际意义时，贝叶斯模型更符合数据，强调了使用适当的统计方法来准确解释脑电数据的重要性。图5清晰展示了当电极效应没有实际意义时，贝叶斯模型对数据更为忠实。图5A针对RR条件直接拟合，结果显示贝叶斯地形图中没有显示出任何效应，而ITPC地形图中存在变化，可能被误解为局部活动，尽管该条件在短语频率上没有任何结构。图5B中的四组模拟数据集结果显示，贝叶斯结果更接近于真实情况，而ITPC结果显示出可能被误解的变化。

图5. 无信号时电极效应的比较。(A)使用随机单词条件（RR）的短语数据的地形头盖。当使用试验间相位相干性（ITPC）计算相位相干性时，整个颅骨的电极存在明显的高但具有误导性的变化。由于电极效应的正则化，这在贝叶斯结果中没有表现出来。(B)数据从生成贝叶斯模型中进行了四次模拟，电极效应设置为零，以提供一个已知的地面真相。图1−4可以被认为是四个独立实验的结果。在此模拟数据上，ITPC表现出类似于(A)的变化；贝叶斯结果与地面真相一致。ITPC有一个向上的偏差，所以在所有的数字中，为了便于比较，都减去了平均值。

采样器诊断

采样器诊断在使用MCMC计算后验时非常重要，因为有时候采样器可能会停留在参数空间的某一部分，这可能导致计算结果出现偏差。在这项研究中，并未出现任何问题：采样成功的最常用度量是ˆR，通常称为R-帽。这是一种比较链的均值和方差的收敛度量，理想情况下应为1.0，但通常<1.05被认为是可以接受的，<1.02则更为理想。在这里，所有的R-帽值均<1.006，表明混合效果良好；这些数值在图6A中有所呈现；图6C展示了每种参数类型中具有最大R-帽值的链；这些图中似乎都没有显示出与采样不良相关的病态行为，链条都是稳定且收敛的。另一个衡量采样成功的指标是比较哈密顿边缘和过渡概率，如图6B所示；这也表明了良好的采样效果。关于树深度警告。

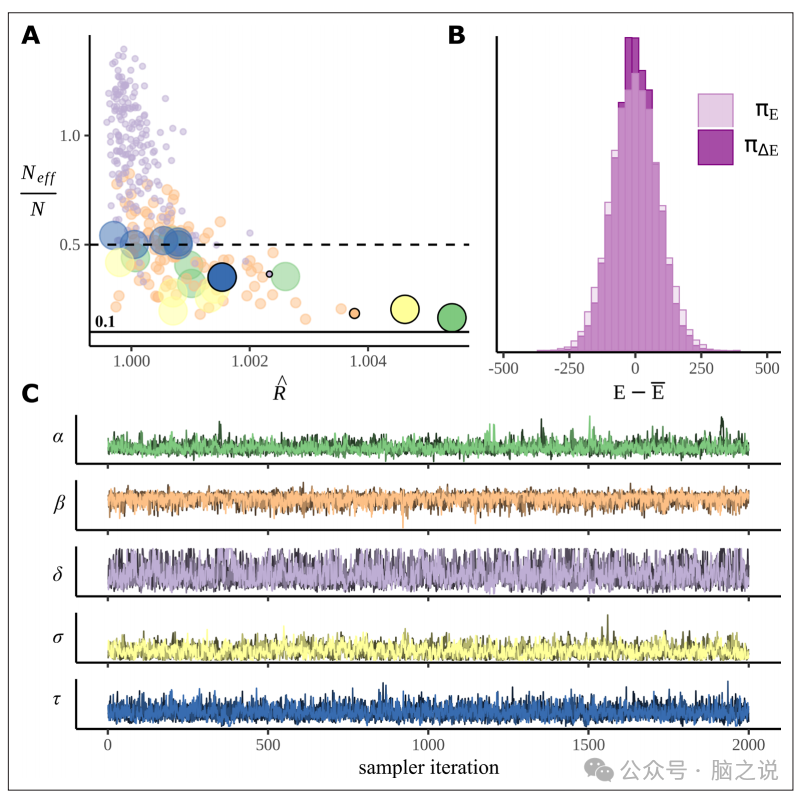
图6. 采样器的性能和诊断方法。(A)通过绘制ˆR（R-hat）与模型中每个参数的有效样本数的比值来说明采样器的性能。点表示每个参数类型按不同颜色分组的各个模型参数。为了方便起见，点的大小是缩放的，所以参数越多，点就越小，数量就越少，例如，只有6个例子的αc就很大。(B)比较哈密顿量的边缘能量分布的πE和过渡能量分布的π∆E的直方图。(C)预热后跟踪图。对于每个参数组中性能最差的参数的所有四个链都被覆盖。(A)中相应的点用黑色边框和零透明度标记。

案例研究：人工语言的统计学习

在这个案例研究中，针对图2中的短语数据，我们对该数据集进行了标准的ITPC分析。在图7A中，我们使用单侧t检验复制了Pinto等人在2022年的原始统计分析，针对每个频率进行了检验。由于ITPC的取值范围在0到1之间，因此它不符合正态分布，因此我们还呈现了Wilcoxon符号秩检验的结果。在音节频率（4 Hz）上，无论是BL条件还是EXP条件都表现出强烈的响应；然而，统计检验结果比较复杂。在伪词频率（1.33 Hz）上可以观察到轻微的相干性增加，在第二谐波（5.33 Hz）上甚至更强。在第一谐波（2.66 Hz）上，BL和EXP之间没有显著差异，尽管有四名参与者在这个频率上表现出相干性显著增加，超过了数据第75百分位数以上1.5倍IQR的值。图7B中的地形图展示了每个电极上参与者平均ITPC的条件间差异、，并在整个头皮上进行了插值。我们使用基于聚类的置换检验来识别描述条件间平均电极响应差异的显著活动簇。在伪词频率及其第一谐波上并未发现显著的活动簇；然而，在中到前额区域出现了更强的活动簇。

图7.ITPC分析结果

注：在图7中，展示了对39名参与者进行的ITPC分析结果。在图7A中，对伪词频率（1.33 Hz）及其第一和第二谐波（2.66 Hz，5.33 Hz）进行了配对单侧检验，以检验实验条件（EXP）的平均ITPC是否更大。同时，我们还进行了一个单侧检验，以检验基线条件（BL）在音节频率上的ITPC值是否更大。左侧展示了未校正的配对Wilcoxon符号秩检验的显著性值，右侧展示了未校正的配对t检验的显著性值。在图7B中，使用基于聚类的置换检验发现了在4 Hz和5.33 Hz处这两个条件之间的显著电极簇。

贝叶斯分析

针对每个频率，我们使用四个链进行了2000次采样，其中一半用于预热阶段。在采样过程中没有检测到发散的转换，并且收敛诊断ˆR < 1.03。图8A展示了每个频率平均结果长度差异的后验分0布。尽管在伪词频率上后验分布更倾向于大于零的值，但左尾中仍有一些值与没有差异一致。如果我们对后验分布的全部范围感兴趣，计算与其支持的任何参数值相关的总概率会更合适。例如，我们可以从后验样本中计算出P(∆R > 0|y) ≈ 0.956。这个分析表明，在伪词频率上，条件之间的期望差异不大，但存在差异是有可能的。伪词频率的第一谐波明显没有显示出实验组之间的差异。后验分布在零点对称峰值，方差较小。第二谐波显示出组之间最大的差异；零点大约与均值相差3.24个标准差。与ITPC分析一致，音节频率的结果

也显示BL具有比EXP更大的值。在这种情况下，零点大约与均值相差1.59个标准差。

在图8中，展示了对统计学习数据集进行的贝叶斯分析。图8A显示了对EXP - BL条件差异的后验分布，涵盖了所有感兴趣的频率。每种情况下，完整的后验分布由直方图给出，并用其90%最高密度区间（HDI）和后验中位数进行注释。图8B展示了每个条件和感兴趣频率的边际后验分布。图8C插值展示了每个64个电极上EXP - BL差异的后验均值。填充的圆圈标记了那些95% HDI中不包含零的电极。

贝叶斯结果表明在伪词频率的第二谐波中存在统计学习的证据；然而，在伪词频率上的结果并不足以完全排除没有差异的可能性。似乎结论的强度受到一些参与者展示相反效应的限制。在最强的结果中，即5.33 Hz，大多数参与者显示EXP有增强的反应。然而在2.33 Hz和1.33 Hz，表现出相反条件效应的参与者与没有的数量相当。在Pinto等人的研究中，暗示了在单个参与者中难以找到统计学习的证据。参与者后验的高方差在频率内部和跨频率上都支持了这一结论。

仿真研究

使用模拟数据进行的模拟研究。该模型通过减少估计中的偏差来提高性能，并且在模拟数据集中展示了对真实差异的检测能力。此外，还介绍了使用基于模拟的校准（SBC）进行模型校准的方法，以及通过直方图和经验累积分布函数（ECDF）的比较来证明模型的校准性。整体而言，贝叶斯模型在估计和检测方面的优越性，并提供了对模型校准的详细说明

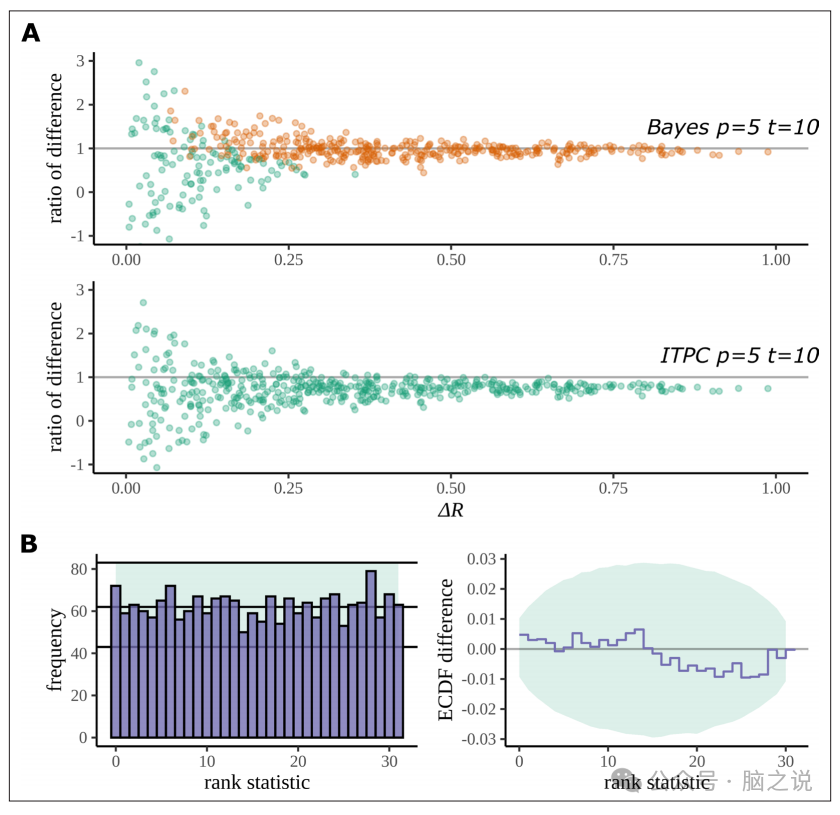
 图9仿真研究。(A)贝叶斯模型对较低的参与者数具有较高的真实检出率。贝叶斯模型也大大减少了估计的偏差。随着实际差异沿x轴增加，两种方法的模型估计的变化都减少了；然而，对于贝叶斯模型来说，这些点在y = 1附近的分布更加对称；这一结果突出了它的偏差减少。他们的轴被限制以帮助突出感兴趣的行为。(B)基于模拟的校准为相同的参与者和试验编号，其中∆R的秩被分析。没有证据表明贝叶斯模型有高估或低估差异的趋势。

讨论

相比于常用的频率分析方法，贝叶斯分析更注重对数据模型参数的估计，并计算我们在进行这些估计时的确定性或不确定性，是一种更为谨慎的数据分析方法，相比于频率分析方法更加谦虚，更注重对数据的实际估计。本研究提出的基于贝叶斯的相位数据描述方法，并使用了神经语言学的具体例子进行说明。这种方法在表达和自然性方面比传统的统计分析方法更好。文章重点关注了神经语言学领域，其中频率标记是常见的，使用了Burroughs等人（2021）的开放数据和一项研究人工语言统计学习存在性的最新研究作为例子。贝叶斯分析在频率标记的多个应用中具有广泛的应用前景，相比于常用的频率分析方法，它更注重对数据模型参数的估计，并计算我们在进行这些估计时的确定性或不确定性。此外，贝叶斯因子在量化特定假设的证据时的有重要作用。

模型扩展

模型进行扩展的可能性包括在统计学习数据集中记录参与者的区块，可以通过增加额外的项来捕捉任何区块效应，或者实现区块和条件之间的交互作用。此外，作者还指出了电极之间存在空间相关性的问题，特别是在较小的数据集中，这一点并不被保证。为了解决这一问题，作者提出了将关于电极位置的先验知识纳入模型的可能性，从而修改当前的独立方法，使之能够编码相邻电极之间的相关响应。

图10. 频率方法和贝叶斯方法在参与者数量方面的效率比较。图中的子图(A)显示了来自两种方法的置信区间，分别是左侧的双边Wilcoxon符号秩检验的置信区间和右侧的贝叶斯最高密度区间，这些区间是针对短语数据集中条件差异AN-RR计算的，分别给出了90/95/99.7%的宽度。子图(B)则展示了相同显著性检验得到的p值（左侧）与通过后验分布观察到小于零的概率（右侧）之间的比较。这些比较有助于展示频率主义方法和贝叶斯方法在处理参与者数量方面的效率和可靠

数据效度

基于贝叶斯方法的脑电分析框架可以更有效地利用数据。通过模拟少量参与者的结果，研究表明，即使由于参与者数量较少而导致频率统计置信区间失败，贝叶斯方法仍然可以检测到条件之间的真实差异。频率方法在确定适当的α值方面存在不确定性，而贝叶斯方法提供了更可靠和高效的分析，特别是在数据有限的情况下。

图11显示了频率主义和贝叶斯方法在试验次数方面的效率比较。图中(A)展示了来自两侧配对Wilcoxon符号秩检验的置信区间（左侧），以及在统计学习数据集中计算的条件差异EXP-BL的贝叶斯最高密度区间（HDI）（右侧）。这些区间给出了90%和95%的置信水平。右侧是相同置信水平下的HDI。图中(B)展示了显著性检验产生的p值（左侧），与后验分布中观察到小于零值的概率（右侧）进行了比较。

总的来说，本文提出的基于贝叶斯方法的脑电分析框架在处理脑电数据方面具有显著的优势。尽管该方法在计算上更具挑战性，需要在模型及其先验的构建上进行一些思考和实验，尤其在频率标记方面更为严格。然而，我们相信贝叶斯描述的清晰度、模型及其证据的完整呈现，以及其提供的出色数据效率，使其成为更优秀的选择。贝叶斯模型在两种情况下特别值得努力：（1）数据有限且嘈杂，因此统计不确定性很高，因此值得明确表示；（2）数据集具有强烈结构，可以设计贝叶斯模型以匹配并在参数之间共享信息。因此，我们相信类似的贝叶斯方法将广泛应用于脑电数据。脑电数据的特性、其嘈杂性、高维度以及参与者数量的倾向使得贝叶斯方法可能会有所帮助。

参考文献：Bayesian analysis of phase data in EEG and MEG.