Diffusion model(一): 公式推导详解

前言

本文一共分为三大部分，这是第一部分

Diffusion model(一): 公式推导详解
Diffusion model(二): 训练推导详解
Diffusion model(三): 公式结论

首先附上几个大佬的讲解
lilianweng-diffusion-models
zhihu_由浅入深了解Diffusion Model
b站_diffusion model 原理讲解
b站_基于 pytorch 动手实现 diffusion model
DDPM论文_NIPS_2020

这篇博客借鉴了上述博客、视频以及DDPM论文，同时加上个人的理解整合了一下，尽可能让整个推导详细，希望能使每个人都看懂

结合之前讲过的VAE和GAN模型，Diffusion Model和他们的区别就是latent code和原图是同尺寸大小的。如下图所示，给大家一个直观的认识：Diffusion Model分为前向过程和反向过程，前向过程将输入图片$x_0$变为纯高斯噪声$x_T$（就是一个不断加噪的过程），反向过程就是将噪声$x_T$还原为图片$x_0$的过程（就是一个不断去噪的过程）

知道Diffusion Model在做什么之后，接下来对Diffusion的前向和反向过程做分析推导

Diffusion的前向过程

1. 前向过程从$x_{t-1}$到$x_t$的公式

给定真实图片$x_0\sim q(x)$，前向过程中diffusion model对其添加了$T$次高斯噪声，分别得到图$x_1,x_2,x_3,...,x_T$（随着$t$的增加，$x$包含越来越多的噪声），这个过程如下表示
$$q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_{t}I)\text{\hspace{1em}(1)}$$

下图展示了前向加噪的过程中图片的变化，从左到右为$x_0,x_1,...,x_T$

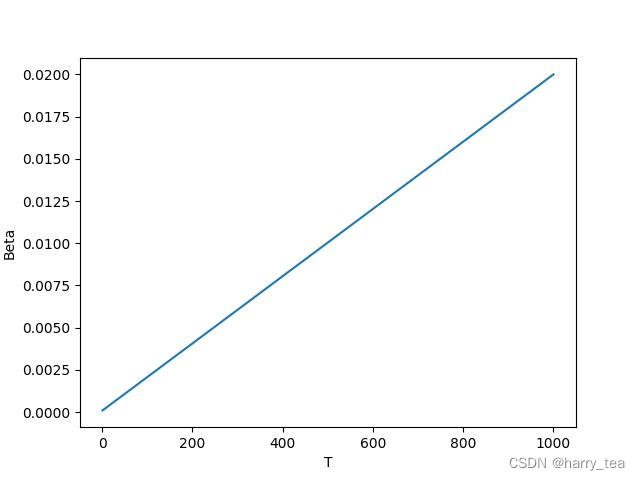
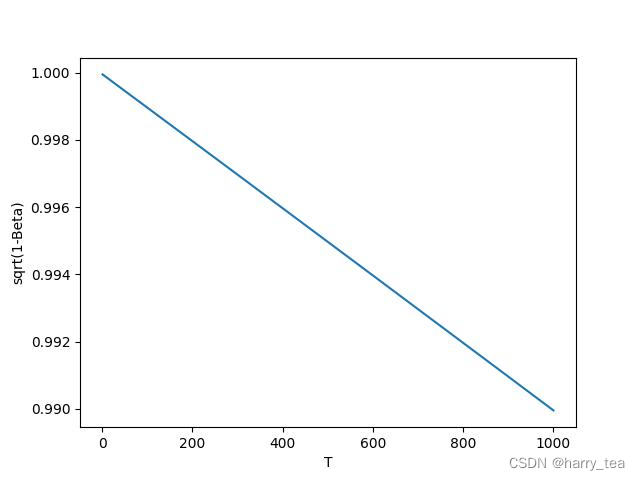
整个前向加噪过程是马尔科夫过程，即$t$时刻的状态只与$t-1$时刻有关，在不断加噪的过程中，$x_t$不断接近纯噪声，$T\to \infty$，$x_t$变为正态分布的高斯噪声（为什么下面会讲），在论文中${\beta }_t$是从0.0001到0.02线性插值的，取$T=1000$，也就是说${\beta }_t$是不断增加的，$1-{\beta }_t$是不断减小的

回过头来再看上述分布$\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_{t}I)$，随着$t$增加，$x_t$的均值是$x_{t-1}$的$\sqrt{1-{\beta }_t}<1$倍，因此最终$x_t$的均值不断变小，趋近于$0$，而标准正态分布的均值也为0

下面是${\beta }_t$和$\sqrt{1-{\beta }_t}$随着$T$增加的变化曲线

2. 怎么从$x_0$直接得到$x_t$的表达式？

前向过程的$T$最多为1000次，如果每次都单独计算过于耗时，这里推导能够一步到位的方式

为了推导方便，原论文令${\alpha }_t=1-{\beta }_t$，${\overline{\alpha }}_t={\prod }_{i=1}^T{\alpha }_i$，并用重参数化的方法来表示前向过程每一步的数据分布（重参数化方法在文末有介绍），这里我们由$q(x_t|x_{t-1})$得
$$\begin{array}{rl}{x}_t& =\sqrt{1-{\beta }_t}{x}_{t-1}+\sqrt{{\beta }_t}{z}_1,where{z}_1,z_2,...,\sim \mathcal{N}(0,I)\\ & =\sqrt{{\alpha }_t}{x}_{t-1}+\sqrt{1-{\alpha }_t}{z}_1\\ & =\sqrt{{\alpha }_t}(\sqrt{{\alpha }_{t-1}}{x}_{t-2}+\sqrt{1-{\alpha }_{t-1}}{z}_2)+\sqrt{1-{\alpha }_t}{z}_1\\ & =\sqrt{{\alpha }_t{\alpha }_{t-1}}{x}_{t-2}+\sqrt{{\alpha }_t}\sqrt{1-{\alpha }_{t-1}}{z}_2+\sqrt{1-{\alpha }_t}{z}_1\\ & =\sqrt{{\alpha }_t{\alpha }_{t-1}}{x}_{t-2}+\sqrt{1-{\alpha }_t{\alpha }_{t-1}}{\overline{z}}_2,{\overline{z}}_2\sim \mathcal{N}(0,I)\\ & =...\\ & =\sqrt{{\alpha }_t{\alpha }_{t-1}...{\alpha }_1}{x}_0+\sqrt{1-{\alpha }_t{\alpha }_{t-1}...{\alpha }_0}{\overline{z}}_t\\ & =\sqrt{{\overline{\alpha }}_t}{x}_0+\sqrt{1-{\overline{\alpha }}_t}{\overline{z}}_t\end{array}\text{\hspace{1em}(2)}$$

公式解释部分，上述公式懂的话可以不看
其中公式的红色部分用到了高斯分布的独立可加性，即$\mathcal{N}(0,{\sigma }_1^{2}I)+\mathcal{N}(0,{\sigma }_2^{2}I)\sim \mathcal{N}(0,({\sigma }_1^2+{\sigma }_2^2)I)$
由
$$\begin{array}{rl}& \sqrt{{\alpha }_t(1-{\alpha }_{t-1})}{z}_2\sim \mathcal{N}(0,{\alpha }_t(1-{\alpha }_{t-1})I)\\ & \sqrt{1-{\alpha }_t}{z}_1\sim \mathcal{N}(0,(1-{\alpha }_{t-1})I)\end{array}$$
可得
$$\sqrt{{\alpha }_t(1-{\alpha }_{t-1})}{z}_2+\sqrt{1-{\alpha }_t}{z}_1\sim \mathcal{N}(0,(1-{\alpha }_t{\alpha }_{t-1})I)\to \sqrt{1-{\alpha }_t{\alpha }_{t-1}}{\overline{z}}_2$$

$x_t$的最终结果为$x_t=\sqrt{{\overline{\alpha }}_t}{x}_0+\sqrt{1-{\overline{\alpha }}_t}{\overline{z}}_t$，其中${\overline{\alpha }}_t={\prod }_{i=1}^T{\alpha }_i$在$T$次连乘之后接近于$0$，即$x_t=0\times x_0+\sqrt{1-0}{\overline{z}}_t={\overline{z}}_t$，即$\mathcal{N}(0,I)$的正态分布，这就是整个前向推导了

3. 关于$x_{t-1}$到$x_t$的一个疑问

为什么$x_t$的分布是$q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_{t}I)$呢？因为这个公式是作者直接给出的，并没有一个推导，公式表明在加噪的过程中均值要乘上$\sqrt{1-{\beta }_t}$，如果要保证均值最后为0的话，只需要每次乘的值小于1就可以了（虽然方差可能并不是$I$），通过上述推导我们可以发现$x_t$的最终等于$\sqrt{{\overline{\alpha }}_t}{x}_0+\sqrt{1-{\overline{\alpha }}_t}{\overline{z}}_t$，即$T\to \infty ,x_t\sim \mathcal{N}(0,I)$，也就是说$\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_{t}I)$这个分布能够保证$x_t$最终收敛为标准高斯分布，但是具体前向分布这个式子怎么得到的，我不是很懂

Diffusion的反向过程

1. 反向过程的理想目标：已知$x_t$，预测$x_{t-1}$

在前向加噪过程中，表达式为$q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_{t}I)$，反向过程就是将上述过程进行逆转，得到$q(x_{t-1}|x_t)$的分布，通过不断的去噪从$x_T\sim \mathcal{N}(0,I)$中还原出原图$x_0$，文中证明了如果$q(x_t|x_{t-1})$满足高斯分布并且${\beta }_t$足够小，$q(x_{t-1}|x_t)$仍然是一个高斯分布。但是我们无法简单推断$q(x_{t-1}|x_t)$，因此我们使用深度学习模型（参数为$\theta$，结构一般为U-net+attention结构）来预测他的真实分布
$$p_{\theta }(x_{t-1}|x_t)=\mathcal{N}(x_{t-1};{\mu }_{\theta }(x_t,t),{\Sigma }_{\theta }(x_t,t))\text{\hspace{1em}(3)}$$

$(3)$式是我们要通过神经网络预测diffusion model反向过程的式子：已知$x_t$以及加噪次数$t$的情况下，推导$x_{t-1}$，这个过程十分复杂，因为我们有无数的去噪可能性，即使最终得到了$x_0$，也无法确定$x_0$是否真的属于$q(x)$这个分布中的数据，因此需要对去噪过程加以限制，即让其去噪后的图片收敛到$q(x)$分布中

2. 额外已知$x_0$的情况下的反向过程

对于反向过程的分布$q(x_{t-1}|x_t)$我们无法预测，但是从前向过程中我们知道$x_0$，所以通过贝叶斯公式得到$q(x_{t-1}|x_t,x_0)$为
$$q(x_{t-1}|x_t,x_0)=(x_{t-1};\tilde{\mu }(x_t,x_0),{\tilde{\beta }}_{t}I)\text{\hspace{1em}(4)}$$

推导过程如下，首先利用贝叶斯公式将反向过程均变为前向过程$x_{t-1}\to x_t$，$x_0\to x_{t-1}$以及$x_0\to x_t$
$$q(x_{t-1}|x_t,x_0)=q(x_t|x_{t-1},x_0)\frac{q(x_{t-1}|x_0)}{q(x_t|x_0)}\text{\hspace{1em}(5)}$$

根据高斯分布的概率密度函数的指数部分$(\mu ,{\sigma }^2)\propto \exp (-\frac{(x-\mu {)}^2}{2{\sigma }^2})$以及前向推导公式$x_t=\sqrt{{\alpha }_t}{x}_{t-1}+\sqrt{1-{\alpha }_t}{z}_1$和$x_t=\sqrt{{\overline{\alpha }}_t}{x}_0+\sqrt{1-{\overline{\alpha }}_t}{\overline{z}}_t$得
$$\begin{array}{rl}q(x_{t-1}|x_t,x_0)& =q(x_t|x_{t-1},x_0)q(x_{t-1}|x_0)\frac{1}{q(x_t|x_0)}\\ & =[\sqrt{{\alpha }_t}{x}_{t-1}+\sqrt{1-{\alpha }_t}{z}_1]\times [\sqrt{{\overline{\alpha }}_{t-1}}{x}_0+\sqrt{1-{\overline{\alpha }}_{t-1}}{\overline{z}}_{t-1}]\times [\frac{1}{\sqrt{{\overline{\alpha }}_t}{x}_0+\sqrt{1-{\overline{\alpha }}_t}{\overline{z}}_t}]\\ & \propto \exp (-\frac{1}{2}(\frac{(x_t-\sqrt{{\alpha }_t}{x}_{t-1}{)}^2}{{\beta }_t}+\frac{(x_{t-1}-\sqrt{{\overline{\alpha }}_{t-1}}{x}_0{)}^2}{1-{\overline{\alpha }}_{t-1}}-\frac{(x_t-\sqrt{{\overline{\alpha }}_t}{x}_0{)}^2}{1-{\overline{\alpha }}_t}))\\ & =\exp (-\frac{1}{2}((\underbrace{\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\overline{\alpha }}_{t-1}})x_{t-1}^2}-\underbrace{(\frac{2\sqrt{{\alpha }_t}}{{\beta }_t}{x}_t+\frac{2\sqrt{{\overline{\alpha }}_{t-1}}}{1-{\overline{\alpha }}_{t-1}}{x}_0)x_{t-1}}+\underbrace{C(x_t,x_0})))\end{array}\text{\hspace{1em}(6)}$$

根据$\exp (-\frac{(x-\mu {)}^2}{2{\sigma }^2})=\exp (-\frac{1}{2}(\frac{1}{{\sigma }^2}{x}^2-\frac{2\mu }{{\sigma }^2}x+\frac{{\mu }^2}{{\sigma }^2}))$，对于大括号中的部分进行化简能够得到$q(x_{t-1}|x_t,x_0)$的均值和方差，如下
$$\{\begin{array}{l}\frac{1}{{\sigma }^2}=\frac{1}{{\tilde{\beta }}_t}=(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\overline{\alpha }}_{t-1}})\\ \\ \frac{2\mu }{{\sigma }^2}=\frac{2{\tilde{\mu }}_t(x_t,x_0)}{{\tilde{\beta }}_t}=(\frac{2\sqrt{{\alpha }_t}}{{\beta }_t}{x}_t+\frac{2\sqrt{{\overline{\alpha }}_{t-1}}}{1-{\overline{\alpha }}_{t-1}}{x}_0)\end{array}\text{\hspace{1em}(7)}$$

化简得
$$\{\begin{array}{l}{\tilde{\beta }}_t=\frac{1-{\overline{\alpha }}_{t-1}}{1-{\overline{\alpha }}_t}\cdot {\beta }_t\\ \\ {\tilde{\mu }}_t(x_t,x_0)=\frac{\sqrt{{\alpha }_t}(1-{\overline{\alpha }}_{t-1})}{1-{\overline{\alpha }}_t}{x}_t+\frac{\sqrt{{\overline{\alpha }}_{t-1}}{\beta }_t}{1-{\overline{\alpha }}_t}{x}_0\end{array}\text{\hspace{1em}(8)}$$
由$x_t=\sqrt{{\overline{\alpha }}_t}{x}_0+\sqrt{1-{\overline{\alpha }}_t}{\overline{z}}_t$，得$x_0=\frac{1}{\sqrt{{\overline{\alpha }}_t}}(x_t-\sqrt{1-{\overline{\alpha }}_t}\overline{z_t})$并替换上面均值中的$x_0$得到
$${\tilde{\mu }}_t=\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{{\beta }_t}{\sqrt{1-{\overline{\alpha }}_t}}{\overline{z}}_t)\text{\hspace{1em}(9)}$$

这样我们证明最初已知$x_0$后的反向表达式了，即
$$\begin{array}{rl}& q(x_{t-1}|x_t,x_0)=(x_{t-1};\tilde{\mu }(x_t,x_0),{\tilde{\beta }}_{t}I)\\ & where\sim {\tilde{\mu }}_t=\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{{\beta }_t}{\sqrt{1-{\overline{\alpha }}_t}}{\overline{z}}_t)\\ & \sim {\tilde{\beta }}_t=\frac{1-{\overline{\alpha }}_{t-1}}{1-{\overline{\alpha }}_t}\cdot {\beta }_t\end{array}\text{\hspace{1em}(10)}$$

观察发现${\alpha }_t$，${\beta }_t$，${\overline{\alpha }}_t$，${\overline{\alpha }}_{t-1}$都是已知的，要想由$x_t$得到$x_{t-1}$未知的只有${\overline{z}}_t$，这也是为什么在反向过程中我们要通过神经网络来预测噪声的原因，预测成功之后我们就可以得到$q(x_{t-1}|x_t,x_0)$的分布了，然后利用重参数技巧来得到$x_{t-1}$

3. 回到第一步的理想目标

通过上述推导发现要得到$x_{t-1}$，反向过程的目的就是预测前向过程每一次t加入的噪声，因此这里的高斯分布${\overline{z}}_t$是深度学习模型所预测的噪声（即重参数化时从标准高斯分布中采样的噪声），可以看做$z_{\theta }(x_t,t)$，由此得到均值为
$${\mu }_{\theta }(x_t,t)=\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{{\beta }_t}{\sqrt{1-{\overline{\alpha }}_t}}{z}_{\theta }(x_t,t))\text{\hspace{1em}(11)}$$

网络的最终目的就是预测$z_{\theta }(x_t,t)$，或者说是均值${\mu }_{\theta }(x_t,t)$，至于方差${\Sigma }_{\theta }(x_t,t)$从推导来看他是一个固定值，论文中也提到当做固定值效果更好