算法学习报告-01 SVD（奇异值分解）

最新推荐文章于 2023-07-17 01:18:05 发布

软件工程师TonnyJack

最新推荐文章于 2023-07-17 01:18:05 发布

阅读量398

点赞数

分类专栏：算法学习笔记文章标签：机器学习线性代数 python

本文链接：https://blog.csdn.net/weixin_42035443/article/details/116050002

版权

算法学习笔记专栏收录该内容

3 篇文章 0 订阅

订阅专栏

SVD（奇异值分解）

简介：

定义：

简介：

奇异值分解(Singular Value Decomposition，以下简称SVD)是在机器学习领域广泛应用的算法，它不光可以用于降维算法中的特征分解，还可以用于推荐系统，以及自然语言处理等领域。是很多机器学习算法的基石。

定义：

在线性代数中，奇异值分解(SVD)是一个实矩阵或复矩阵的因式分解。它是将正半定正规矩阵(如具有正特征值的对称矩阵)的特征分解推广到任意m × n矩阵的极坐标分解。

SVD分解公式：

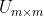
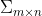
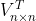
$Data_{m\times n}$ = $U_{m\times m}$ $\Sigma_{m\times n}$ $V_{n\times n}^{T}$

由下图可以直观地理解SVD分解公式：

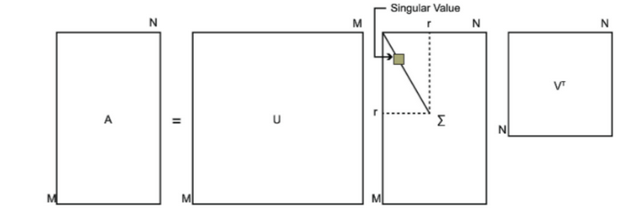
preview

SVD是直接在原始矩阵上进行的矩阵分解，并且能对非方阵矩阵分解，得到左奇异矩阵U、sigma矩阵Σ、右奇异矩阵VT。

奇异值分解可以将一个矩阵 $Data_{m\times n}$ 分解成3个矩阵 $U_{m\times m}$ 、 $\Sigma_{m\times n}$ 、 $V_{n\times n}^{T}$ 。

其中U、 $V^{T}$ 都是单式矩阵（unitary matrix），Σ是一个对角矩阵，也就是说只有对角线有值。对角元素称为奇异值。

M-线性变换分解为 U-旋转 ∑-拉伸 $V^{T}$ -旋转

SVD计算举例：

①定义矩阵 A 为： $A = \begin{pmatrix} 0& 1& \\ 1& 1& \\ 0& 1& \\ \end{pmatrix}$ ，则

$A^{T}A = \begin{pmatrix} 0& 1& 1&\\ 1& 1& 0&\end{pmatrix}\begin{pmatrix} 0& 1& \\ 1& 1& \\ 1& 0& \end{pmatrix}=\begin{pmatrix} 2 & 1 & \\ 1 & 2 & \end{pmatrix}$ ， $AA^{T}=\begin{pmatrix} 0 & 1 & \\ 1 & 1 & \\ 1 & 0 & \end{pmatrix}\begin{pmatrix} 0 & 1 & 1 & \\ 1& 1 & 0 & \end{pmatrix}=\begin{pmatrix} 1 & 1 & 0 & \\ 1 & 2& 1& \\ 0& 1& 1& \end{pmatrix}$

②再分别求出二者的特征值和特征向量：

$A^{T}A$ 的特征值和特征向量为 $\lambda _{1}=3$ ， $v_{1}=\begin{pmatrix} 1/\sqrt{2} & \\ 1/\sqrt{2}& \end{pmatrix}$ , $\lambda _{2}=1$ ， $v_{2}=\begin{pmatrix} -1/\sqrt{2} & \\ 1/\sqrt{2}& \end{pmatrix}$

$AA^{T}$ 的特征值和特征向量为 $\lambda _{1}=3$ ， $u_{1}=\begin{pmatrix} 1/\sqrt{6} & \\ 2/\sqrt{6}&\\ 1/\sqrt{6} \end{pmatrix}$ ， $\lambda _{2}=1$ ， $u_{2}=\begin{pmatrix} 1/\sqrt{2} & \\0\\ -1/\sqrt{2}& \end{pmatrix}$ ， $\lambda _{3}=0$ ， $u_{3}=\begin{pmatrix} 1/\sqrt{3} & \\ -1/\sqrt{3}&\\ 1/\sqrt{3} \end{pmatrix}$

③根据 $Av_{i}=\sigma _{i}u_{i}$ ，i = 1, 2求奇异值：

$\begin{pmatrix} 0& 1& \\ 1& 1& \\ 0& 1& \\ \end{pmatrix}$ $\begin{pmatrix} 1/\sqrt{2} & \\ 1/\sqrt{2}& \end{pmatrix}$ $=\sigma _{1}$ $\begin{pmatrix} 1/\sqrt{6} & \\ 2/\sqrt{6}&\\ 1/\sqrt{6} \end{pmatrix}$ 解得 $\sigma _{1}=\sqrt{3}$

$\begin{pmatrix} 0& 1& \\ 1& 1& \\ 0& 1& \\ \end{pmatrix}$ $\begin{pmatrix} -1/\sqrt{2} & \\ 1/\sqrt{2}& \end{pmatrix}$ $=\sigma _{2}$ $\begin{pmatrix} 1/\sqrt{2} & \\ 0&\\ -1/\sqrt{2} \end{pmatrix}$ 解得 $\sigma _{2}=1$

④最终可得到A的奇异值分解为： $A=U\sum ^{}V^{T}=$ $\begin{pmatrix} 1/\sqrt{6} & 1/\sqrt{2} & 1/\sqrt{3} & \\ 2/\sqrt{6} & 0& -1/\sqrt{3} & \\ 1/\sqrt{6} & -1/\sqrt{2} & 1/\sqrt{3} \end{pmatrix}$ $\begin{pmatrix} \sqrt{3}& 0& \\ 0& 1& \\ 0& 0& \end{pmatrix}$ $\begin{pmatrix} 1/\sqrt{2} & 1/\sqrt{2} & \\ -1/\sqrt{2} & 1/\sqrt{2} & \end{pmatrix}$

SVD编程实现（Python）：

import numpy                                          # 导入numpy库及linalg包
from numpy import linalg as la

A = numpy.mat(numpy.array([[0, 1], [1, 1], [0, 1]]))  # 初始化矩阵
U, Sigma, VT = la.svd(A)                              # 使用linalg里的svd函数可求出A的SVD分解
print("U = \n", U)                                    # 打印U，Sigma及VT
print("\nSigma = \n", Sigma)
print("\nVT = \n", VT)

输出结果：

U =
[[ 0.5 -0.5 -0.70710678]
[ 0.70710678 0.70710678 0. ]
[ 0.5 -0.5 0.70710678]]

Sigma =
[1.84775907 0.76536686]

VT =
[[ 0.38268343 0.92387953]
[ 0.92387953 -0.38268343]]

进程已结束，退出代码为 0