Logistic回归公式推导和代码实现和Python中的sklearn.linear_model.LogisticRegression 的参数

1，引言

logistic回归是机器学习中最常用最经典的分类方法之一，有人称之为逻辑回归或者逻辑斯蒂回归。虽然他称为回归模型，但是却处理的是分类问题，这主要是因为它的本质是一个线性模型加上一个映射函数Sigmoid，将线性模型得到的连续结果映射到离散型上。它常用于二分类问题，在多分类问题的推广叫softmax。
　　本文首先阐述Logistic回归的定义，然后介绍一些最优化算法，其中包括基本的梯度上升法和一个改进的随机梯度上升法，这些最优化算法将用于分类器的训练，最好本文将给出一个Logistic回归的实例，预测一匹病马是否能被治愈。
　　在我们的日常生活中遇到过很多最优化问题，比如如何在最短时间内从A点到达B点？如何投入最少工作量却获得最大的效益？如何设计发动机使得油耗最少而功率最大？可见，最优化的作用十分强大，所以此处我们介绍几个最优化算法，并利用它们训练出一个非线性函数用于分类。
　　现在假设有一些数据点，我们用一条直线对这些点进行拟合（该线称为最佳拟合直线），这个拟合过程就称作回归。利用logistic回归进行分类的主要思想是：根据现有数据对分类边界线建立回归公式，以此进行分类，这里的“回归”一词源于最佳拟合，表示要找到最佳拟合参数集。训练分类器时的做法就是寻找最佳拟合参数，使用的是最优化算法，下面我们首先介绍一下这个二值型输出分类器的数学原理。
那么逻辑回归与线性回归是什么关系呢？
逻辑回归（Logistic Regression）与线性回归（Linear Regression）都是一种广义线性模型（generalized linear model）。逻辑回归假设因变量 y 服从伯努利分布，而线性回归假设因变量 y 服从高斯分布。 因此与线性回归有很多相同之处，去除Sigmoid映射函数的话，逻辑回归算法就是一个线性回归。可以说，逻辑回归是以线性回归为理论支持的，但是逻辑回归通过Sigmoid函数引入了非线性因素，因此可以轻松处理0/1分类问题。

2，Logistic回归的一般过程

• （1）收集数据：采用任意方法收集数据

• （2）准备数据：由于需要进行距离计算，因此要求数据类型为数值型。另外，结构化数据格式则最佳

• （3）分析数据：采用任意方法对数据进行分析

• （4）训练算法：大部分时间将用于训练，训练的目的是为了找到最佳的分类回归系数

• （5）使用算法：首先，我们需要输入一些数据，并将其转换成对应的结构化数值；接着，基于训练好的回归系数就可以对这些数值进行简单的回归计算，判定他们属于哪个类别；在这之后，我们就可以在输出的类别上做一些其他分析工作。

3，Logistic回归的优缺点

**优点：**计算代码不多，易于理解和实现，计算代价不高，速度快，存储资源低
　　**缺点：**容易欠拟合，分类精度可能不高
　　**适用数据类型：**数值型和标称型数据

4，基于Logistic回归和Sigmoid函数的分类

**我们想要的函数应该是：能接受所有的输入，然后预测出类型。**例如，在两个类的情况下，上述函数输出0或1。该函数称为海维赛德阶跃函数（Heaviside step function），或者直接称为单位阶跃函数。然而，海维赛德阶跃函数的问题在于：该函数在跳跃点上从0瞬间跳跃到1，这个瞬间跳跃过程有时很难处理。幸好，另一个函数也有类似的性质（可以输出0或者1），且数学上更易处理，这就是Sigmoid函数。Sigmoid函数具体的计算公式如下：
　　自变量取值为任意实数，值域[0, 1]
　　图5-1给出了Sigmoid函数在不同坐标尺度下的两条曲线图。当x为0时，Sigmoid函数值为0.5。随着x的增大，对应的Sigmoid值将逼近于1；而随着x的减少，Sigmoid值将逼近于0.如果横坐标刻度足够大，Sigmoid函数看起来很像一个阶跃函数。

**解释Sigmoid函数：**将任意的输入映射到了 [0, 1]区间，我们在线性回归中可以得到一个预测值，再将该值映射到 Sigmoid函数中这样就完成了由值到概率的转换，也就是分类任务。
　　因此，为了实现Logistic回归分类器，我们可以在每个特征上都乘以一个回归系数，然后把所有的结果值相加，将这个总和带入Sigmoid函数中，进而得到一个范围在0~1之间的数值。任何大于0.5的数据被分入1类，小于0.5即被归入0类，所以，Logistic回归也可以被看成是一种概率估计。
　　确定了分类器的函数形式之后，现在的问题变成了：最佳回归系数是多少？如何确定其大小。

5，基于最优化方法的最佳回归系数确定

Sigmoid函数的输入记为z，由下面公式得到：

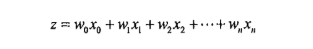
如果采用向量的写法，上述公式可以写成 z = wTx ，它表示将这两个数值向量对应元素相乘，然后全部加起来即得到z值。

　　其中的向量x是分类器的输入数据，向量w也就是我们要找到的最佳参数（系数），从而使得分类器尽可能的准确，为了寻找该最佳参数，需要用到最优化理论的一些知识。
　　然后再看看我们的Logistic回归模型的公式：

　　这里假设 W>0，Y与X各维度叠加的图形关系，如下图所示（x为了方便取1维）：

　　下面首先学习梯度上升的最优化方法，我们将学习到如何使用该方法求得数据集的最佳参数，接下来，展示如何绘制梯度上升法产生的决策边界图，该图将梯度上升法的分类效果可视化的呈现出来，最后我们将学习随机梯度上升算法，以及如何对其进行修改以获得很好地结果。

• 可能我们最常听到的是梯度下降算法，它与这里的梯度上升算法是一样的，只是公式中的加法需要变成减法，梯度上升算法用来求函数的最大值，而梯度下降算法是用来求函数的最小值

6，梯度上升法

梯度上升法基于的思想是：要找到某函数的最大值，最好的方法是沿着该函数的梯度方向探寻，如果梯度记为，则函数 f(x,y) 的梯度由下面式子表示：

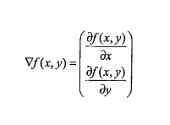
这个梯度意味着要沿着x的方向移动
，沿着y方向移动
，其中函数f(x,y)必须要在待计算的点上有定义并且可微，一个具体的函数例子见图5-2：

　　上图中的梯度上升算法沿梯度方向移动了一步，可以看出，梯度算子总是指向函数值增长最快的方向。这里所说的移动方向，而未提到移动量的大小。该量值称为步长，记为。用向量来表示的话，梯度算法的迭代公式如下：

　　该公式将一直被迭代执行，直至达到某个停止条件为止，比如迭代次数达到某个指定值或算法达到某个可以允许的误差范围。
　　基于上面的内容，我们来看一个Logistic回归分类器的应用例子，从图5-3可以看到我们采用的数据集。

梯度上升法的公式推导（LR 损失函数）
　　在LR中，应用极大似然估计法估计模型参数，由于Sigmoid函数的特性，我们可以做如下的假设：

上式即为在已知样本X和参数θ的情况下。样本X属性正类（y=1）和负类（y=0）的条件概率，将两个公式合并成一个，如下：

　　假定样本与样本之间相互独立，那么整个样本集生成的概率即为所有样本生成概率的乘积（也就是n个独立样本出现的似然函数如下）：

　　为了简化问题，我们对整个表达式求对数（即为LR 损失函数）：

　　满足似然函数（θ）的最大的θ值即时我们需要求解的模型。
　　那么梯度上升法就像爬坡一样，一点一点逼近极值，而上升这个动作用数学公式表达即为：

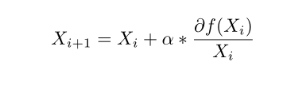
　　其中，α 为步长。

回到Logistic回归问题，我们同样对函数求偏导。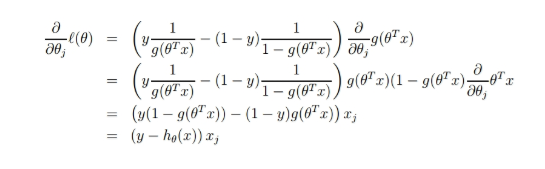
对这个公式进行分解，先看：

　　我们可以看到，对函数求偏导，分解为三部分，然后我们对这三部分分布求导。

其中：

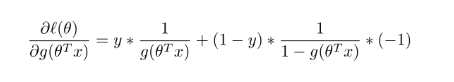
再由：

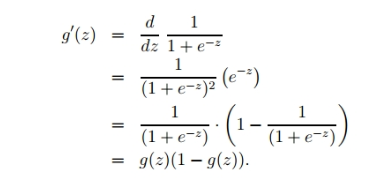
可得：

接下来：
最后：

综合三部分即得到：

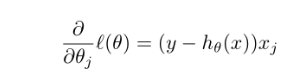
　　如果上面链式分解不好理解的话，可以看下面直接求导（结果是一样的）：

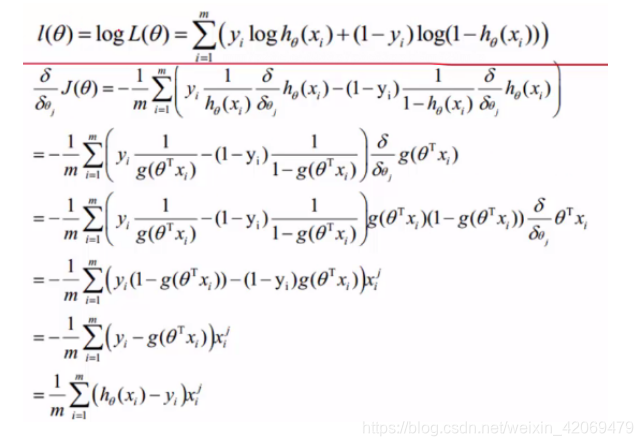
　　注意上面是将梯度上升求最大值，转换为梯度下降了，本质没变。
因此梯度迭代公式为：

如果为梯度下降，我们注意符号的变化，如下：

7，训练算法：使用梯度上升找到最佳参数

上图有100个样本点，每个点包含两个数值型特征：X1和X2，在此数据集上，我们将通过使用梯度上升法找到最佳回归系数，也就是拟合出Logistic回归模型的最佳参数。

所以我们的目标：建立分类器，求解出theta参数
　　设定阈值，根据阈值判断结果

8 Python中的sklearn.linear_model.LogisticRegression

sklearn.linear_model.LogisticRegression官方API：http://scikitlearn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html

class sklearn.linear_model.LogisticRegression(penalty='l2', dual=False, tol=0.0001, C=1.0,fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None,solver='liblinear', max_iter=100, multi_class='ovr', verbose=0,warm_start=False, n_jobs=1)

ogistic回归（aka logit，MaxEnt）分类器。

在多类情况下，如果将“ multi_class”选项设置为“ ovr”，则训练算法将使用“一对多休息”（OvR）方案；如果将“ multi_class”选项设置为“多项式”，则使用交叉熵损失’。（当前，只有“ lbfgs”，“ sag”，“ saga”和“ newton-cg”求解器支持“多项式”选项。）

该类使用“ liblinear”库，“ newton-cg”，“ sag”，“ saga”和“ lbfgs”求解器实现正则逻辑回归。请注意，默认情况下将应用正则化。它可以处理密集和稀疏输入。使用C排序的数组或包含64位浮点数的CSR矩阵可获得最佳性能；其他任何输入格式将被转换（并复制）。

“ newton-cg”，“ sag”和“ lbfgs”求解器仅支持带有原始公式的L2正则化，不支持正则化。'liblinear’求解器支持L1和L2正则化，仅针对L2罚分采用对偶公式。仅“ saga”求解器支持Elastic-Net正则化。


笔记

底层的C实现在拟合模型时使用随机数生成器选择特征。因此，对于相同的输入数据具有略微不同的结果并不罕见。如果发生这种情况，请尝试使用较小的tol参数。

在某些情况下，预测输出可能与独立liblinear的输出不匹配。请参见 叙述文档中与liblinear的区别。

参考文献

L-BFGS-B –大规模约束优化软件
朱次有，理查德·伯德，豪尔赫·诺德达尔和何塞·路易斯·莫拉莱斯。 http://users.iems.northwestern.edu/~nocedal/lbfgsb.html

LIBLINEAR –大型线性分类的库
https://www.csie.ntu.edu.tw/~cjlin/liblinear/

凹陷-马克·施密特（Mark Schmidt），尼古拉斯·勒·鲁（Nicolas Le Roux）和弗朗西斯·巴赫（Francis Bach）
用随机平均梯度最小化有限求和 https://hal.inria.fr/hal-00860051/document

SAGA – Defazio，A.，Bach F.和Lacoste-Julien S.（2014）。
SAGA：一种支持非强凸复合物镜的快速增量梯度方法 https://arxiv.org/abs/1407.0202

于祥富，黄芳兰，林志仁（2011）。双坐标下降
逻辑回归和最大熵模型的方法。机器学习85（1-2）：41-75。 https://www.csie.ntu.edu.tw/~cjlin/papers/maxent_dual.pdf

例子

>>> from sklearn.datasets import load_iris
>>> from sklearn.linear_model import LogisticRegression
>>> X, y = load_iris(return_X_y=True)
>>> clf = LogisticRegression(random_state=0).fit(X, y)
>>> clf.predict(X[:2, :])
array([0, 0])
>>> clf.predict_proba(X[:2, :])
array([[9.8...e-01, 1.8...e-02, 1.4...e-08],
       [9.7...e-01, 2.8...e-02, ...e-08]])
>>> clf.score(X, y)
0.97...

• 使用实例sklearn.linear_model.LogisticRegression