数学笔记：集合运算性质的证明，有理数集合的性质

首先看第一个证明，要证明一个结果，常用的方法是看看哪个结果跟这个要证明的结果是等价的。
浏览上次的笔记，可以发现：

也就是说，必须证明

现在，问题被简化成证明左边是右边的子集，且，右边是左边的子集

要证明左边要是右边的子集，那么左边任意一个元素都必须从属于右边这个集合
所以它证明时，使用了一个任取，这个任取非常关键。

这样，再回顾它的证明过程，思路就清晰的多了。

这里重要的不是死记住，而是理解证明的思路，无非就是一堆等价中间结果的推导而已。
所以数学最重要的就是记住性质，因为数学是非常严格且精密的，性质全记住了，其它证明操作也就是各种性质的推导罢了。

那后边这个，我就照猫画虎，自己证明一下试试。

1，左边是右边的子集，且右边是左边的子集
2，左边任意一个元素必须是右边这个集合的元素
（1）
任取x从属于左边
∵x从属于A交B的余集
∴x不属于A交B
∴x从属于A的余集或x从属于B的余集
∴x从属于A的余集并B的余集
∴左边是右边的子集
（2）
任取x从属于右边
∵x从属于A的余集并B的余集
∴x从属于全集
∴右边范围比左边大
∴证明失败！= =

？？？？what？？哪里出了问题？我还是看一下答案吧。。。。

哦，看到这里我发现，之所以证明不出来，是因为我忘了一个性质：

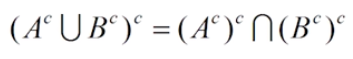
而且，我认为A的余集并B的余集就是全集，说明对余集的理解还不够充分。
而且，我的空间想象能力不够，把图像想错了，其实画个图就明白了。


发现中间那块儿区域并没有被标注，，，，，，，

然后我检查上一篇博客，发现根本没有记这个公式，第一节视频上也没讲，第二节直接让你用，= =
巧妇难为无米之炊，我还能无中生有乎…我太难了

第二种证明方法：

X是全集，
X\A 是X减去A（差集）

全集减去A等于A的余集，所以最后等于A的余集交B的余集，左边等于右边，证明完毕。

然后给出了一个定理

这里边用到了上节没讲的重要的规律：

重要规律1

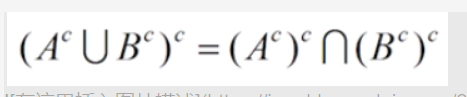
总结一下就是：
A和B并集的余集，等于A的余集交B的余集
A和B交集的余集，等于A的余集并B的余集
再总结一下就是：
要拆分某个表达式外边的余集符号，就得把里边的每一个都取余集，并且交变并，并变交

重要规律2

有理数集合的性质