【吴恩达机器学习笔记】第二章 多变量线性回归

【吴恩达机器学习笔记】第二章 多变量线性回归

1、多元线性回归的假设形式

我们假设多变量线性回归的假设形式如下所示：
$$h_{\theta }\left(x\right)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+\cdots +{\theta }_n{x}_n$$为了方便我们将$x_0$定义为1

则可设向量$x=\left[\begin{array}{l}{x}_0\\ x_1\\ x_2\\ ⋮\\ x_n\end{array}\right]$$\theta =\left[\begin{array}{l}{\theta }_0\\ {\theta }_1\\ {\theta }_2\\ ⋮\\ {\theta }_n\end{array}\right]$

则原假设形式也可以写为$h_{\theta }\left(x\right)={\theta }^{T}x$

2、代价函数

多元线性回归的代价函数与单变量线性回归相似，其如下所示：
$$J\left(\theta \right)=\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }\left(x^{\left(i\right)}\right)-y^{\left(i\right)}\right)}^2$$
其中 $\theta$ 为一个维度为 $n+1$ 的向量

3、梯度下降

重复直到找到局部最优解{$${\theta }_j:={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m\left(h_{\theta }\left(x^{\left(i\right)}\right)-y^{\left(i\right)}\right)x_j^{\left(i\right)}$$$$(同步更新{\theta }_{j}forj=0,...n)$$}

4、特征缩放

百度百科中的对特征缩放(Feature Scaling)的解释为

特征缩放是用来统一资料中的自变项或特征范围的方法，在资料处理中，通常会被使用在资料前处理这个步骤。因为在原始的资料中，各变数的范围大不相同。

一般情况下，我们执行特征缩放时，我们通常的目的是，将特征的取值约束到-1到1的范围内。
但是-1和1的数字并不是很重要，比这个范围大一点或小一点 都没问题，只是不要差距太大就行，如以下例子：

特征缩放的方法有多种，我比较习惯使用标准化方法，具体公式如下所示：$$x_i\to \frac{x_i-\min }{\max -\min }$$

5、确保梯度下降算法正确执行的方法

为了确定梯度下降算法的正常运行，我们通常会生成一张$\min J\left(\theta \right)$随迭代次数变化而变化的图像，如下图所示：

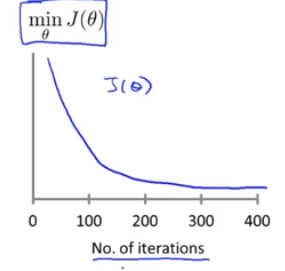
只有当此函数单调递减时，梯度下降算法才是正确执行的。也可以通过此图像判断算法完成的迭代次数。

我们也可以使用自动收敛测试来判断算法是否收敛完成。如果代价函数在某一次迭代之后，小于一个很小的值 $\epsilon$,这个测试就判断函数已经收敛。$\epsilon$通常是$10^{-3}$。但是要选择一个正确合适的阈值是很困难的，所以还是比较建议通过看上面这种函数图像来判断。

另外，如果生成的$\min J\left(\theta \right)$随迭代次数变化而变化的图像不是单调递减，在确保代码无误的前提下，最好的办法是减小学习率 $\alpha$。

我们通常选择学习率 $\alpha$ 大小变化为$\cdots 0.001,0.01,0.1,1\cdots$，在迭代正确的情况下，选择尽可能大的学习率 $\alpha$。

6、特征和多项式回归

当一个数据图像如下图所示时：

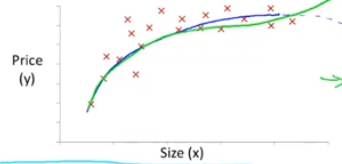
我们可能会使用多项式回归模型来进行拟合，例如 ${\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2+{\theta }_3{x}^3$，那么如何使用多元线性回归模型进行拟合呢？

我们可以对模型进行一些修改来实现它，如下所示：$$\begin{array}{l}{h}_{\theta }\left(x\right)={\theta }_0+{\theta }_{1}x+{\theta }_{2}x+{\theta }_{3}x={\theta }_0+{\theta }_1(size)+{\theta }_2(size{)}^2+{\theta }_3(size{)}^3\\ x_1=(size)\\ x_2=(size{)}^2\\ x_3=(size{)}^3\end{array}$$在这种情况下，特征缩放就会非常重要了，因为$x_1,x_2,x_3$的大小会差别非常大。

7、正规方程（Normal equation）

前文对于线性规划的参数，我们是采用梯度下降通过迭代来求解，而本篇中的正规方程提供了一种 $\theta$ 的解析解法，因此我们可以不用多次迭代算法，而是可以一次性的求解 $\theta$ 的最优值。

要运用此方程，我们首先要构建两个向量 $X$，$y$，那么要如何构建呢？假设我们有 $m$ 个数据样本$\left(x^{\left(1\right)},y^{\left(1\right)}\right),\cdots \left(x^{\left(m\right)},y^{\left(m\right)}\right);$每条数据分别有$n$个特征值。那么向量 $x$、向量 $X$ 和向量 $y$ 分别为：$$x^{\left(i\right)}=\left[\begin{array}{l}{x}_0^{\left(i\right)}\\ x_1^{\left(i\right)}\\ x_2^{\left(i\right)}\\ ⋮\\ x_n^{\left(i\right)}\end{array}\right]\in R^{n+1}X=\left[\begin{array}{l}{\left(x^{\left(1\right)}\right)}^T\\ {\left(x^{\left(2\right)}\right)}^T\\ ⋮\\ {\left(x^{\left(m\right)}\right)}^T\end{array}\right]y=\left[\begin{array}{l}{y}^{\left(1\right)}\\ y^{\left(2\right)}\\ ⋮\\ y^{\left(m\right)}\end{array}\right]$$则向量 $\theta$ 为：$$\theta ={\left(X^{T}X\right)}^{-1}{X}^{T}y$$Octave上的计算正规方程的代码为：pinv(X’*X)*X*y。即使$\left(X^{T}X\right)$不可逆，pinv函数也可以算出想要的 $\theta$ 值。

$\left(X^{T}X\right)$不可逆的原因：
（1）有多余的特征变量。例如：$x_1$=面积（平方英尺），$x_2$=面积（平方米）
（2）特征变量过多。列如：样本量小于特征变量个数（$m<n$）。
解决方法：减少一些特征变量或使用正则化方法（regularzation），此方法以后会进行介绍。

如果使用正规方程法，则可以不用进行特征缩放。

梯度下降和正规方程的优缺点：

梯度下降	正规方程
优点：在特征变量很多的情况下，也能运行的非常好	优点：不需要选择学习速率 $\alpha$，可以一次性求解所以不用运行很多次，也不用画出代价函数的变化图像来检查函数收敛性。
缺点：需要选择合适的学习速率 $\alpha$，意味着需要运行很多次找到效果最好的，这是一种额外的工作和麻烦 。	缺点：需要计算计算${\left(X^{T}X\right)}^{-1}$，而当计算机计算逆矩阵时，需要的代价是以矩阵维度的三次方增长$\left(O(n^3)\right)$。所以当 $n$ 很大时（比如大于10000时），计算会非常慢