【吴恩达机器学习笔记】第三章 Logistic回归

【吴恩达机器学习笔记】第三章 Logistic回归

Logistic回归虽然叫做回归，但实际上是一种分类算法。

1、假设函数

假设： $h_{\theta }(x)=g({\theta }^{T}x)$
Logistic函数（也称sigmoid函数）如下所示：$$g\left(z\right)=\frac{1}{1+e^{-z}}$$图像大致为：

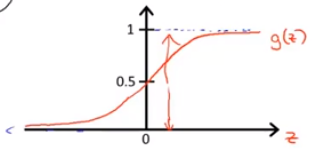
这样可以使 $h_{\theta }\left(x\right)$的范围在0到1之间。

$h_{\theta }\left(x\right)$的含义用概率来解释为：$h_{\theta }\left(x\right)=p\left(y=1|\theta ;x\right)$

2、决策界限

如果我们要预测输出的值为0还是为1，我们可以假设：
如果 $h_{\theta }\left(x\right)\ge 0.5$，那么 $y=1$；如果 $h_{\theta }\left(x\right)<0.5$，那么 $y=0$

根据Logistic函数图像可以发现，$h_{\theta }\left(x\right)\ge 0.5$ 时，$x\ge 0$，$h_{\theta }\left(x\right)<0.5$ 时，$x<0$

举个例子让我们能更直观的理解，假设有一个数据集如图所示：

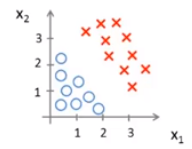
假设函数为 $h_{\theta }\left(x\right)=g\left({\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2\right)$，假设$\theta =\left[\begin{array}{c}-3\\ 1\\ 1\end{array}\right]$。
那么当 $g\left({\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2\right)\ge 0$，即 $-3+x_1+x_2\ge 0$ 时，可以预测 $y=1$。
$x_1+x_2\ge 3$的意义是在图中划了一条线，将数据集进行了二分类，如下图所示：

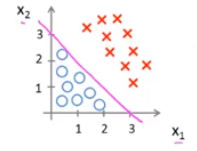
红线上面的区域为假设函数预测 $y=1$ 的区域，下面为假设函数预测 $y=0$ 的区域，这条红线则被成为决策边界，它对应了一系列 $h_{\theta }\left(x\right)=0.5$ 的点
决策边界不是数据集的属性而是假设本身及其参数的属性
如果 $\theta$ 参数比较复杂，决策边界也会变得更复杂，而不一定是一条直线。

3、代价函数

因为 Logistic函数 $g\left(z\right)=\frac{1}{1+e^{-z}}$ 是非常非线性的，如果将线性回归的代价函数：$$J\left(\theta \right)=\frac{1}{m}\sum _{i=1}^{m}Cost(h_{\theta }(x^{(i)}),y^{(i)})$$$$Cost(h_{\theta }(x^{(i)}),y^{(i)})=\frac{1}{2}(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$来作为 Logistic回归的代价函数，画出的代价函数图像是非凸函数，如下图所示：

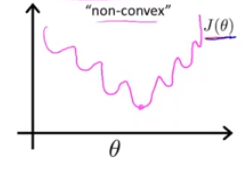
它有多个局部最优点，如果用梯度下降算法会很容易陷入局部最优解，为了使代价函数能够为凸函数，我们定义 Logistic回归的代价函数如下：$$Cost(h_{\theta }(x),y)=\{\begin{array}{c}-log(h_{\theta }(x))ify=1\\ -log(1-h_{\theta }(x))ify=0\end{array}$$我们画出代价函数图像如下所示：

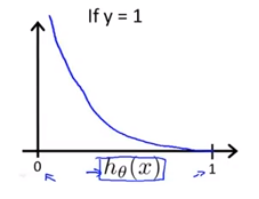
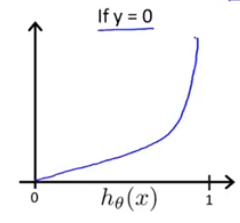
为了使代价函数不分段，我们做了简化后得到新的代价函数：$$Cost(h_{\theta }(x),y)=-ylog(h_{\theta }(x))-(1-y)log(1-h_{\theta }(x))$$

4、梯度下降算法

我们已经得到 Logistic回归的代价函数如下所示：$$J(\theta )=-\frac{1}{m}[\sum _{i=1}^m{y}^{(i)}log(h_{\theta }(x^{(i)}))+(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]$$我们按照前面所学的梯度下降算法的模板：

repeat: ${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J(\theta )$

带入Logistic回归的代价函数后发现与线性回归的梯度下降算法几乎一样：

repeat: ${\theta }_j:={\theta }_j-\alpha {\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$

不同之处在于：线性回归的 $h_{\theta }(x)$ 是 ${\theta }^{T}X$，而Logistic回归的 $h_{\theta }(x)$ 是 $\frac{1}{1+e^{-{\theta }^{T}X}}$

同样，在线性回归中的特征缩放在Logistic回归中也同样适用。

5、高级优化算法

举个栗子：假设有$$\theta =\left[\begin{array}{c}{\theta }_1\\ {\theta }_2\end{array}\right]$$$$J(\theta )=({\theta }_1-5{)}^2+({\theta }_2-5{)}^2$$$$\frac{\partial }{\partial {\theta }_1}J(\theta )=2({\theta }_1-5)$$$$\frac{\partial }{\partial {\theta }_2}J(\theta )=2({\theta }_2-5)$$
则用高级优化算法的MATLAB代码如下所示：

costFunction.m

function [jVal,gradient] = costFunction(theta)
jVal = (theta(1)-5)^2 + (theta(1)-5)^2;
gradient = zeros(2,1);
gradient(1) = 2*(theta(1)-5);
gradient(2) = 2*(theta(2)-5);

main.m

options = optimset('GradObj','on','MaxIter',100);
initialTheta = zeros(2,1);
[optTheta,functionVal,exitFlag]=fminunc(@costFunction,initialTheta,options);

6、多元分类

假设我们有训练集

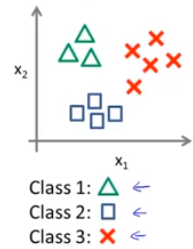
我们可以分别拟合出三个分类器如下所示：

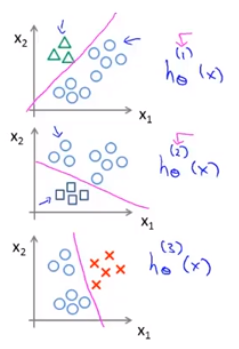
我们得到一个拟合分类器：
$$h_{\theta }^{(i)}(x)=P(y=i|x;\theta )$$
总结:
如果要进行多元分类，我们可以训练一个逻辑回归分类器 $h_{\theta }^{(i)}(x)$ 预测 i 类别 $y=i$的概率。
最后为了做出预测，我们给定一个新的输入值 x， 我们要做的就是，在每个分类器运行输入x，然后选择 $h$ 最大的类别，也就是要选择分类器。