向量表示 运动抛物线_高考真题，向量在抛物线中的妙用，向量优势，你还愁圆锥曲线吗？...

01原题再现

［全国三卷文科2019·21］已知曲线C：y=x^2/2，D为直线y=－1/2上的动点，过D作C的两条切线，切点分别为A，B.

⑴证明：直线AB过定点；

⑵若以E(0,5/2)为圆心的圆与直线AB相切，且切点为线段 AB的中点，求该圆的方程。

图一

这道题是一个直线与圆锥曲线的题，该题共分为两问，这里两问都有一定的难度。

其中第一问是解答第二问的基础，需要根据第一问得出直线AB含字母的方程，这里的第一问如果解答不出，后面更是无法解答。

而该第一问是要证明直线AB过定点，且条件较少，想完全求出直线AB的方程不太可能，不过是求证直线AB过定点，不一定非要求出直线AB的完整方程，只要确定该方程的一部分即可。

虽然如此，但是使用常规方法也很难得出直线AB的部分方程。

所以这里使用了新方法去证明第一问，以及得出第二问需要的直线AB的部分方程——这种方法需要大家注意！

而第二问是需要借助向量的方法来解决，否则会因未知量多而无法解决，即使可解决也会带来“繁琐”的计算。

在这道题中，使用向量的方法，也充分地体现了向量的优势——有时使用向量的方向向量即可解决，从而减少了没有必要的未知量！

下面我们就一起看看具体的做法。

02第一问巧解

第一问可以根据斜率相等建立等量关系。

图二

第一步，根据导数公式得出过A，B的切线斜率。

因为抛物线的方程为y=x^2/2，则一次导数y＇=x。

设A(x1,y1)，B(x2,y2)，则过A点的切线DA的斜率为k1=x1；过B点的切线DB的斜率为k2=x2.

第二步，根据两点得出过A，B的切线斜率。

因为D点在y=－1/2动直线上，则可设D(t,－1/2)。

根据两点坐标得出直线DA的斜率：k1=(y1+1/2)/(x1－t).

由第一步可知，k1=x1，则有(y1+1/2)/(x1－t)=x1，整理得到

2tx1－2y1+1=0。

根据两点坐标得出直线DB的斜率：k2=(y2+1/2)/(x2－t).

由第一问可知，k2=x2，则有(y2+1/2)/(x2－t)=x2，整理得到

2tx2－2y2+1=0。

第三步，得出直线AB的方程。

由2tx1－2y1+1=0和2tx2－2y2+1=0可知，点A，B都是方程2tx－2y+1=0地解。

根据两点确定一条直线的原则，则有直线AB的方程为2tx－2y+1=0。

第四步，得出直线AB过定点。

令x=0，则y=1/2.

——之所以令x=0，是因为当x=0时，无论t为何值时2tx的数值不变。

所以直线AB过定点(0,1/2)。

03向量在第二问中的秒用

第二问分析：

第二问给出的一个已知圆心E(0,5/2)的圆与直线AB：2tx－2y+1=0相切，而切点恰好是直线AB的中点，求此时的圆E的方程。

要想求出该圆的方程，就是要求出该圆的半径。

这里的圆心已经给出主要就是求直线AB的中点坐标，再根据两点间距离公式得出该圆的半径。

由于直线AB中存在字母t，经求解直线AB的中点也是带有字母的t的，也就是得出直线AB的中点依然是未知的。

那如何建立关于t的等式得出t的值呢？

这里常规的方式是很难建立等量关系求出t的值，所以要使用向量的方向性来解答——即两个向量垂直，只需要两个向量的方向向量垂直即可。

第二问解题步骤：

第一步，求出直线AB的中点坐标——用字母t表示。

由第一问可知，直线AB的方程为y=tx+1/2。

将直线AB的方程与抛物线的方程y=x^2/2联立，则有

x^2－2tx－1=0.

根据韦达定理，则有x1+x2=2t，x1x2=－1。

因为y=tx+1/2，则有y1+y2=t(x1+x2)+1=2t^2+1。

设直线AB的中点为M(x0,y0)，根据中点坐标运算，则有

x0=(x1+x2)/2=t，y0=(y1+y2)/2=t^2+1/2.

所以直线AB的中点坐标M(t,t^2+1/2)。

第二步，根据向量的方向向量求出t的数值。

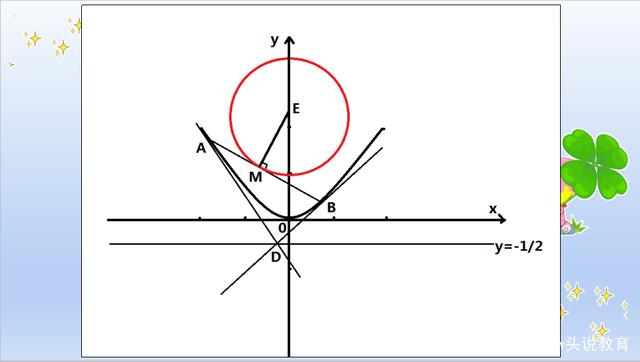图三

因为AB是圆E的切线，所以连接EM，则EM⊥AB，即向量EM·向量AB=0.

根据向量坐标运算，则有

向量EM=(t,t^2+1/2)－(0,5/2)=(t,t^2－2)；

向量AB=(x2,y2)－(x1,y1)=(x2－x1,y2－y1)。

注：这里向量AB的坐标含有的未知量较多，所以这一步将向量AB用相同方向的向量来表示，因为向量EM和向量AB同一个方向的向量也是垂直的。

向量AB=(x2－x1)(1,t)，则向量AB可用向量(1，t)来代替，因为它们的方向相同，也满足向量EM与向量(1，t)垂直。

注：根据题意，x1≠x2。

则有向量EM·向量(1，t)=(t,t^2－2)·(1，t)=0.

整理得到t·(t^2－1)=0，解得到t=0或者t=±1.

第三步，根据t的值得出圆E的方程。

当t=0时，M点坐标为(0，1/2)，根据两点距离公式，则有|EM|=2，则此时圆E的方程为x^2+(y－5/2)^2=4；

当t=±1时，M点坐标为(1，3/2)和(－1,3/2)，根据两点距离公式，则有|EM|=√2，此时圆E的方程为x^2+(y－5/2)^2=2.

综上所述，该圆的方程为x^2+(y－5/2)^2=4或x^2+(y－5/2)^2=2。

04总结

上述的题中需要注意的点有：

第一，第一问方法的使用；

第二，第二问中求参数t的过程，根据相同向量具有相同的方向性，将向量AB更换成向量(1,t)，从而减少不必要的已知，建立关于t的等式。

相关文章：

高中数学：隐形圆在三种情况下的使用，资料都没的重点你要错过？

高中：两条直线位置关系类型题大全，三大突破点是解这类题的关键

求证动圆过定点？这样转化大题变送分题！向量在综合题中的巧用

中点在抛物线中的巧用，带你简化计算，节省时间，这就是差距来源

向量在椭圆上的巧妙构建，充分体现向量和椭圆的性质，神奇的简化

#高中数学#