二叉树的深度和直径等

111-二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

方法一：深度优先搜索

首先可以想到使用深度优先搜索的方法，遍历整棵树，记录最小深度。

对于每一个非叶子节点，我们只需要分别计算其左右子树的最小叶子节点深度。这样就将一个大问题转化为了小问题，可以递归地解决该问题。

class Solution {
public:
    int minDepth(TreeNode *root) {
        if (root == nullptr) {
            return 0;
        }

        if (root->left == nullptr && root->right == nullptr) {
            return 1;
        }

        int min_depth = INT_MAX;
        if (root->left != nullptr) {
            min_depth = min(minDepth(root->left), min_depth);
        }
        if (root->right != nullptr) {
            min_depth = min(minDepth(root->right), min_depth);
        }

        return min_depth + 1;
    }
};

class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        
        if not root.left and not root.right:
            return 1
        min_depth = 10**9
        if root.left:
            min_depth = min(self.minDepth(root.left), min_depth)
        if root.right:
            min_depth = min(self.minDepth(root.right), min_depth)
        
        return min_depth + 1

1. 时间复杂度：O(N)，其中 N 是树的节点数。对每个节点访问一次。
2. 空间复杂度：O(H)，其中 HH 是树的高度。空间复杂度主要取决于递归时栈空间的开销，最坏情况下，树呈现链状，空间复杂度为 O(N)。平均情况下树的高度与节点数的对数正相关，空间复杂度为 O(logN)。

方法二：广度优先搜索

class Solution {
public:
    int minDepth(TreeNode *root) {
        if (root == nullptr) {
            return 0;
        }

        queue<pair<TreeNode *, int> > que;
        que.emplace(root, 1);
        while (!que.empty()) {
            TreeNode *node = que.front().first;
            int depth = que.front().second;
            que.pop();
            if (node->left == nullptr && node->right == nullptr) {
                return depth;
            }
            if (node->left != nullptr) {
                que.emplace(node->left, depth + 1);
            }
            if (node->right != nullptr) {
                que.emplace(node->right, depth + 1);
            }
        }

        return 0;
    }
};

class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0

        que = collections.deque([(root, 1)])
        while que:
            node, depth = que.popleft()
            if not node.left and not node.right:
                return depth
            if node.left:
                que.append((node.left, depth + 1))
            if node.right:
                que.append((node.right, depth + 1))
        
        return 0

1. 时间复杂度：O(N)，其中 N 是树的节点数。对每个节点访问一次。
2. 空间复杂度：O(N)，其中 N 是树的节点数。空间复杂度主要取决于队列的开销，队列中的元素个数不会超过树的节点数。

104-二叉树的最大深度

给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

方法一：深度优先搜索

思路与算法

如果我们知道了左子树和右子树的最大深度 l和 r，那么该二叉树的最大深度即为

								max(l,r)+1

而左子树和右子树的最大深度又可以以同样的方式进行计算。因此我们可以用「深度优先搜索」的方法来计算二叉树的最大深度。具体而言，在计算当前二叉树的最大深度时，可以先递归计算出其左子树和右子树的最大深度，然后在 O(1) 时间内计算出当前二叉树的最大深度。递归在访问到空节点时退出。

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr) return 0;
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};

class Solution:
    def maxDepth(self, root):
        if root is None: 
            return 0 
        else: 
            left_height = self.maxDepth(root.left) 
            right_height = self.maxDepth(root.right) 
            return max(left_height, right_height) + 1 

1. 时间复杂度：O(n)，其中 n 为二叉树节点的个数。每个节点在递归中只被遍历一次
2. 空间复杂度：O(height)，其中height 表示二叉树的高度。递归函数需要栈空间，而栈空间取决于递归的深度，因此空间复杂度等价于二叉树的高度。注：深度是从上到下数的，而高度是从下往上数。

方法二：广度优先搜索

我们也可以用「广度优先搜索」的方法来解决这道题目，但我们需要对其进行一些修改，此时我们广度优先搜索的队列里存放的是「当前层的所有节点」。每次拓展下一层的时候，不同于广度优先搜索的每次只从队列里拿出一个节点，我们需要将队列里的所有节点都拿出来进行拓展，这样能保证每次拓展完的时候队列里存放的是当前层的所有节点，即我们是一层一层地进行拓展，最后我们用一个变量ans 来维护拓展的次数，该二叉树的最大深度即为ans。

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr) return 0;
        queue<TreeNode*> Q;
        Q.push(root);
        int ans = 0;
        while (!Q.empty()) {
            int sz = Q.size();
            while (sz > 0) {
                TreeNode* node = Q.front();Q.pop();
                if (node->left) Q.push(node->left);
                if (node->right) Q.push(node->right);
                sz -= 1;
            }
            ans += 1;
        } 
        return ans;
    }
};

1. 时间复杂度：O（n）
2. 空间复杂度：O（n），满二叉树时，队列中存储的数量是最多的（<n）

543-二叉树的最大直径

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

方法一：深度优先搜索

首先我们知道一条路径的长度为该路径经过的节点数减一，所以求直径（即求路径长度的最大值）等效于求路径经过节点数的最大值减一。

而任意一条路径均可以被看作由某个节点为起点，从其左儿子和右儿子向下遍历的路径拼接得到

如图我们可以知道路径 [9, 4, 2, 5, 7, 8] 可以被看作以 2 为起点，从其左儿子向下遍历的路径 [2, 4, 9] 和从其右儿子向下遍历的路径 [2, 5, 7, 8] 拼接得到。

假设我们知道对于该节点的左儿子向下遍历经过最多的节点数 L （即以左儿子为根的子树的深度） 和其右儿子向下遍历经过最多的节点数 R （即以右儿子为根的子树的深度），那么以该节点为起点的路径经过节点数的最大值即为 L+R+1 。

我们记节点 node 为起点的路径经过节点数的最大值为dnode，那么二叉树的直径就是所有节点 dnode的最大值减一。

最后的算法流程为：我们定义一个递归函数 depth(node) 计算dnode，函数返回该节点为根的子树的深度。先递归调用左儿子和右儿子求得它们为根的子树的深度 L 和 R ，则该节点为根的子树的深度即为

该节点的 dnode值为

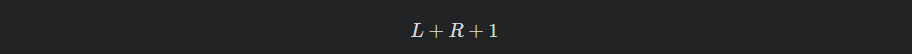
递归搜索每个节点并设一个全局变量ans 记录dnode 的最大值，最后返回 ans-1 即为树的直径。

class Solution {
    int ans;
    int depth(TreeNode* rt){
        if (rt == NULL) {
            return 0; // 访问到空节点了，返回0
        }
        int L = depth(rt->left); // 左儿子为根的子树的深度
        int R = depth(rt->right); // 右儿子为根的子树的深度
        ans = max(ans, L + R + 1); // 计算d_node即L+R+1 并更新ans
        return max(L, R) + 1; // 返回该节点为根的子树的深度
    }
public:
    int diameterOfBinaryTree(TreeNode* root) {
        ans = 1;
        depth(root);
        return ans - 1;
    }
};

1. 时间复杂度：O(N)，其中 N 为二叉树的节点数，即遍历一棵二叉树的时间复杂度，每个结点只被访问一次。
2. 空间复杂度：O(n)，平均复杂度为O（height）,其中 Height 为二叉树的高度。由于递归函数在递归过程中需要为每一层递归函数分配栈空间，所以这里需要额外的空间且该空间取决于递归的深度，而递归的深度显然为二叉树的高度，并且每次递归调用的函数里又只用了常数个变量，所以所需空间复杂度为 O(Height)，最坏情况下，时间复杂度为O（n） 。

124-二叉树中的最大路径和

路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

方法一：递归

和543-二叉树的直径思路大致类似
首先，考虑实现一个简化的函数 maxGain(node)，该函数计算二叉树中的一个节点的最大贡献值，具体而言，就是在以该节点为根节点的子树中寻找以该节点为起点的一条路径，使得该路径上的节点值之和最大。

具体而言，该函数的计算如下。

空节点的最大贡献值等于 0。
非空节点的最大贡献值等于节点值与其子节点中的最大贡献值之和（对于叶节点而言，最大贡献值等于节点值）。
上述计算过程是递归的过程，因此，对根节点调用函数 maxGain，即可得到每个节点的最大贡献值。

根据函数 maxGain 得到每个节点的最大贡献值之后，如何得到二叉树的最大路径和？对于二叉树中的一个节点，该节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值，如果子节点的最大贡献值为正，则计入该节点的最大路径和，否则不计入该节点的最大路径和。维护一个全局变量 maxSum 存储最大路径和，在递归过程中更新 maxSum 的值，最后得到的 maxSum 的值即为二叉树中的最大路径和。
例如：

class Solution {
private:
    int maxSum = INT_MIN;

public:
    int maxGain(TreeNode* node) {
        if (node == nullptr) {
            return 0;
        }
        
        // 递归计算左右子节点的最大贡献值
        // 只有在最大贡献值大于 0 时，才会选取对应子节点
        int leftGain = max(maxGain(node->left), 0);
        int rightGain = max(maxGain(node->right), 0);

        // 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值
        int priceNewpath = node->val + leftGain + rightGain;

        // 更新答案
        maxSum = max(maxSum, priceNewpath);

        // 返回节点的最大贡献值
        return node->val + max(leftGain, rightGain);
    }

    int maxPathSum(TreeNode* root) {
        maxGain(root);
        return maxSum;
    }
};

class Solution {
private:
    int maxSum = INT_MIN;

public:
    int maxGain(TreeNode* node) {
        if (node == nullptr) {
            return 0;
        }
        
        // 递归计算左右子节点的最大贡献值
        // 只有在最大贡献值大于 0 时，才会选取对应子节点
        int leftGain = max(maxGain(node->left), 0);
        int rightGain = max(maxGain(node->right), 0);

        // 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值
        int priceNewpath = node->val + leftGain + rightGain;

        // 更新答案
        maxSum = max(maxSum, priceNewpath);

        // 返回节点的最大贡献值
        return node->val + max(leftGain, rightGain);
    }

    int maxPathSum(TreeNode* root) {
        maxGain(root);
        return maxSum;
    }
};

1. 时间复杂度：O（n）
2. 空间复杂度：O（n）,最坏情况下，时间复杂度为O（n） 。