算法技巧-前缀和数组

560-和为K的子数组

给你一个整数数组 nums 和一个整数 k ，请你统计并返回该数组中和为 k 的连续子数组的个数。

方法一：枚举

因为是子数组，可以循环遍历所有子数组的和，找到符合条件的子数组。

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int count = 0;
        for (int start = 0; start < nums.size(); ++start) {
            int sum = 0;
            for (int end = start; end >= 0; --end) {
                sum += nums[end];
                if (sum == k) {
                    count++;
                }
            }
        }
        return count;
    }
};

1. 时间复杂度：O（n^2）
2. 空间复杂度：O（1）

方法二：前缀和+哈希表优化

我们可以基于方法一利用数据结构进行进一步的优化，我们知道方法一的瓶颈在于对每个 i，我们需要枚举所有的 j 来判断是否符合条件，这一步是否可以优化呢？答案是可以的。

我们定义 pre[i] 为[0…i] 里所有数的和，则 pre[i] 可以由pre[i−1] 递推而来，即：

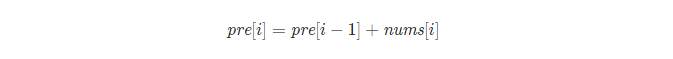
那么[j…i] 这个子数组和为 k ，这个条件我们可以转化为
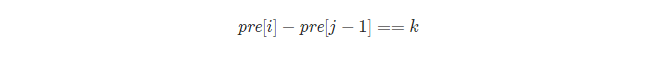简单移项可得符合条件的下标 j需要满足

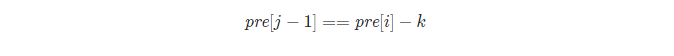
所以我们考虑以 i 结尾的和为 k 的连续子数组个数时只要统计有多少个前缀和为pre[i]−k 的 pre[j] 即可。我们建立哈希表 mp，以和为键，出现次数为对应的值，记录pre[i] 出现的次数，从左往右边更新 mp 边计算答案，那么以 i 结尾的答案pre[i]−k] 即可在 O(1) 时间内得到。最后的答案即为所有下标结尾的和为 k 的子数组个数之和。

需要注意的是，从左往右边更新边计算的时候已经保证了mp[pre[i]−k] 里记录的pre[j] 的下标范围是 0≤j≤i 。同时，由于pre[i] 的计算只与前一项的答案有关，因此我们可以不用建立pre 数组，直接用 pre 变量来记录pre[i−1] 的答案即可。

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        unordered_map<int, int> mp;
        mp[0] = 1;
        int count = 0, pre = 0;
        for (auto& x:nums) {
            pre += x;
            if (mp.find(pre - k) != mp.end()) {
                count += mp[pre - k];
            }
            mp[pre]++;
        }
        return count;
    }
};

1. 时间复杂度：O(n)，其中 n 为数组的长度。我们遍历数组的时间复杂度为 O(n)，中间利用哈希表查询删除的复杂度均为 O(1)，因此总时间复杂度为 O(n)。
2. 空间复杂度：O(n)，其中 n 为数组的长度。哈希表在最坏情况下可能有 n 个不同的键值，因此需要 O(n) 的空间复杂度。

304-二维区域和检索-矩阵不可变

给定一个二维矩阵 matrix，以下类型的多个请求：

计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。

实现 NumMatrix 类：

NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化 int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。

方法一：一维前缀和

创建 m行 n+1 列的二维数组sums，其中 m 和 n 分别是矩阵 matrix 的行数和列数，sums[i] 为 matrix[i] 的前缀和数组。将sums 的列数设为n+1 的目的是为了方便计算每一行的子数组和，不需要对 col1 =0 的情况特殊处理。

class NumMatrix {
public:
    vector<vector<int>> sums;

    NumMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size();
        if (m > 0) {
            int n = matrix[0].size();
            sums.resize(m, vector<int>(n + 1));
            for (int i = 0; i < m; i++) {
                for (int j = 0; j < n; j++) {
                    sums[i][j + 1] = sums[i][j] + matrix[i][j];
                }
            }
        }
    }

    int sumRegion(int row1, int col1, int row2, int col2) {
        int sum = 0;
        for (int i = row1; i <= row2; i++) {
            sum += sums[i][col2 + 1] - sums[i][col1];
        }
        return sum;
    }
};

1. 时间复杂度：O（mn）,其中 m 和 n分别是矩阵 matrix 的行数和列数。
2. 空间复杂度：O（mn）