无约束一维极值——牛顿型法

牛顿型法包括牛顿法和阻尼牛顿法。这类方法的最大优点是收敛速度快，即它的迭代次数相对于其他方法来说少得多。特别是对于一些性态较好的目标函数,例如二次函数,只需保证求梯度和二阶偏导数矩阵时的精度,不管初始点在何处,均可一步就找出最优点。可是这类方法也有很大的缺点,在每次迭代决定牛顿方向时,都要计算目标函数的一阶导数和二阶导数矩阵及其逆矩阵。这就使计算度较为复杂,增加了每次迭代的计算工作量和计算机存储量。

1.牛顿法

牛顿法是根据目标函数的等值线在极值点附近是同心椭圆族的特点,在极值点X’邻域内用一个二次函数φ(X)来近似代替原目标函数f(X),并将φ(X)的极小值点作为对目标函数f(X)求优的下一个迭代点,经多次迭代,使之逼近原目标函数f(X)的极小值点。

例 函数 F(x)=exp(x1²+x1+x2²-3)名 以x0=[1,2]T为初始点,用牛顿法对其进行迭代

根据题意编写代码：

syms x1 x2
f = exp(x1^2+x1+3*x2^2-3);
v = [x1,x2];
df = jacobian(f,v);
df=df.';
G= jacobian(df, v);
epson = 1e-12;
xm=[0,0]';
g1 = subs(df, {x1,x2}, {xm(1,1),xm(2,1)});
G1 = subs(G, {x1,x2}, {xm(1,1),xm(2,1)});
k=0;
while(norm(g1)> epson)
	p = -G1\g1;
	xm = xm + p;
	g1 = subs(df, {x1,x2},{xm(1,1),xm(2,1)});
	G1 = subs(G,{x1,x2}, {xm(1,1),xm(2,1)});
	k=k+ 1;
end
k
xm

运行后得到结果如下

即经过4次迭代,找到了该函数的极小值点。

2.阻尼牛顿法

对于二次函数,用牛顿法迭代一次即可得到最优点；对于非二次函数,若函数的迭代点已进入极小值点的邻域,则其收敛速度也是很快的。但是从牛顿法迭代公式的推导过程可以看出,迭代点是由近似二次函数φ(X)的极值条件确定的，该点可能是φ(X)极小值点,也可能是φ(X)的极大值点。因此在用牛顿法迭代时，可能会出现函数上升的现象,即f(X^（K+1)> f(X^(K)),使迭代不能收敛于最优点。

牛顿法不能保证函数值稳定地下降，在严重的情况下甚至不能收敛而导致计算失败。可见,牛顿法对初始点的要求是比较苛刻的,所选取的初始点离极小值点不能太远。而在极小值点位置未知的情况下，上述要求很难达到。

为了消除牛顿法的这些弊端,需要对其做一些修改。将牛顿法定步长的迭代,改为变步长的迭代,引入步长a,在X^(K)的牛顿方向进行一维搜索 ,保证每次迭代点的函数值都是下降的。这种方法称为阻尼牛顿法,其迭代公式为

式中,ak为牛顿方向的最优步长。这种方法对初始点的选取不再苛刻,从而提高了牛顿法的可靠度。但采用阻尼牛顿法,每次迭代都要进行一维搜索 ,使收敛速度大大降低。

例如,对于某些目标函数,取同样的初始点，采用阻尼牛顿法进行迭代，达到同样的精度,要经过多次的迭代,越靠近极小值点收敛速度越慢,使牛顿法收敛速度快的优势损失殆尽。

根据以上步骤,阻尼牛顿法的MATLAB程序如下:

function [x, f, k]= dampnm( fun, gfun, Hess, x0)
maxk= 500;              %最大迭代次数
rho =0.55;
sigma =0.4;
k=0;
epsilon = 1e-5;              %计算精度
while( k < maxk)            %判断选代次数是否满足是定值
	gk = feval(gfun, x0);	%函数f在x0的梯度
	Gk = feval(Hess, x0);	%函数f在x0的海瑟矩阵(Hessian)
	dk = -Gk\gk;			%解方程组-gk= Gk* dk
	if( norm(gk)< epsilon)  %判断终止迭代准则，是否满足设定精度
        break; 
    end
	m=0;mk= 0;
	while(m < 20)            %运用Armijo法做非精度线搜索，确定步长因子
        if(feval(fun,x0+ rho^m*dk) < feval(fun,x0) + sigma* rho^m*gk'*dk)
            mk = m;
            break;
        end
        m=m+1;
    end
    x0=x0+ rho^mk*dk;
    k=k+1;
end
x = x0;             %赋值最后迭代点
f= feval(fun,x);    %计算最后迭代点x的函数值
end

例 已 知无约束优化问题的目标函数是f(x)=50(x1²一x2)²+(x1一3)²，求在初始迭代点x⁽⁰⁾=[1,1]^T下,迭代次数不超过500次的目标函数最优值。

解:在MATLAB中依次建立目标函数代码

• 建立目标函数f(x)的MATLAB代码:

function f = fun(x)
f = 50*(x(1)^2-x(2))^2 + (x(1)-3)^2;

• 建立目标函数的梯度的matlab代码：

function g = mfun(x)
g = [400*x(1) * (x(1)^2-x(2))+ 2*(x(1)-1), -200*(x(1)^2-x(2))]';

• 建立目标函数Hessian矩阵的MATLAB代码:

function He = Hfun(x)
n= length(x);
He= zeros(n,n);
He= [1200*x(1)^2- 400 *x(2) + 2,-400*x(1); -400*x(1), 200];

调用上面的程序,在MATLAB命令窗口中输人:

clear all
clc
x0=[1 1]';
[x,f,k] = dampnm( 'fun','mfun', 'Hfun' ,x0)

得到结果：

得到在x⁽⁰⁾ =[1,1]^T下,迭代次数不超过500次的目标函数最优值为4。

使用MATLAB中提供的优化工具箱fminunc函数，也可以实现上述结果。
调用fminune函数程序代码如下:

clear all
clc
x0= [0 1];
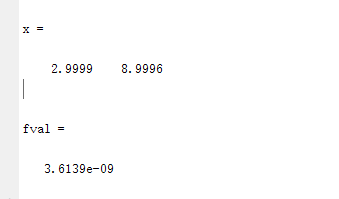
[x, fval] = fminunc( @ fun, x0)