点到线段的距离_中考热点，精准透析线段最值求解八策略，值得关注

初中几何中的最值问题是指在一定条件下，求平面几何图形中某个意义明确的量(如线段的长度、角度大小、图形面积等)的最大值或最小值.几何最值问题属于中考题中的热点问题，其中，求线段的最值问题是近几年常见的题型，且这类问题内容丰富，知识点多，涉及面广，解法灵活多样，具有一定的难度。本文拟例谈这类问题的求解策略，给这个特殊中考复习提供一个加油站。

策略1利用"两点之间，线段最短"求线段最值

【模型1展示】

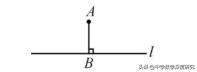
A，B是直线l两侧的两个定点，P是直线l上一动点，当P，A，B三点在一条直线上时，PA+PB最小等于AB.

【模型2展示】

A，B是直线/同侧的两个定点，P是直线l上一动点，当A，B，P三点在一条直线上时，PA-PB最大等于AB.

1.(2019秋•垦利区期中)我国古代有这样一道数学问题："枯木一根直立地上高二丈四尺，周六尺，有葛藤自根缠绕而上，三周而达其顶，问葛藤之长几何？"题意是：如图，把枯木看作一个圆柱体，因一丈是十尺，则该圆柱的高为24尺，底面周长为6尺，有葛藤自点A处缠绕而上，绕三周后其末端恰好到达B处，则问题中葛藤的最短长度是______尺．

【解析】：此类问题应先根据题意把立体图形展开成平面图形后，再确定两点之间的最短路径．一般情况是两点之间，线段最短．在平面图形上构造直角三角形解决问题．如图所示，在如图所示的直角三角形中，

∵BC＝24尺，AC＝6×3＝18尺，

答：葛藤长为30尺．

故答案为：30．

2.(2019•黄冈)如图，AC，BD在AB的同侧，AC＝2，BD＝8，AB＝8，点M为AB的中点，若∠CMD＝120°，则CD的最大值是_______．

【解析】：如图，作点A关于CM的对称点A′，点B关于DM的对称点B′．

∵∠CMD＝120°，∴∠AMC+∠DMB＝60°，

∴∠CMA′+∠DMB′＝60°，∴∠A′MB′＝60°，

∵MA′＝MB′，∴△A′MB′为等边三角形

∵CD≤CA′+A′B′+B′D＝CA+AM+BD＝2+4+8＝14，

∴CD的最大值为14，故答案为14．

策略2利用"垂线段最短"求最值

【模型展示】

直线l处有一定点A，点B是l上一动点，当AB⊥ｌ时，AB最短。

3．(2019•红花岗区校级二模)如图，直角三角形ABC中，AC＝2，BC＝4，P为斜边AB上一动点，PE⊥BC，PF⊥CA，则线段EF长的最小值为(　　)

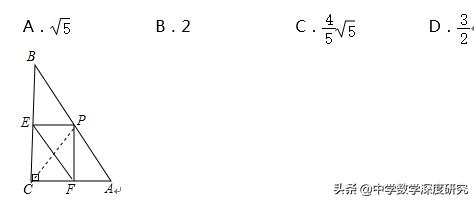
【解析】：连接PC，如图所示：∵PE⊥BC，PF⊥CA，

∴∠PEC＝∠PFC＝∠C＝90°，∴四边形ECFP是矩形，

∴EF＝PC，∴当PC最小时，EF也最小，

∵垂线段最短，∴当CP⊥AB时，PC最小，

4．(2019•泰安)如图，矩形ABCD中，AB＝4，AD＝2，E为AB的中点，F为EC上一动点，P为DF中点，连接PB，则PB的最小值是(　　)

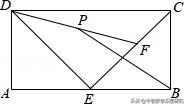
A．2 B．4 C．√2 D．2√2

【解析】：如图：

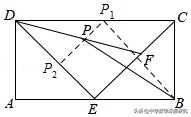
当点F与点C重合时，点P在P₁处，CP₁＝DP₁，

当点F与点E重合时，点P在P2处，EP₂＝DP₂，

∴P₁P₂∥CE且P₁P₂＝1/2CE

当点F在EC上除点C、E的位置处时，有DP＝FP

由中位线定理可知：P₁P∥CE且P₁P＝1/2CF

∴点P的运动轨迹是线段P₁P₂，∴当BP⊥P₁P₂时，PB取得最小值

∵矩形ABCD中，AB＝4，AD＝2，E为AB的中点，

∴△CBE、△ADE、△BCP₁为等腰直角三角形，CP₁＝2，

∴∠ADE＝∠CDE＝∠CP₁B＝45°，∠DEC＝90°，

∴∠DP₂P₁＝90°，∴∠DP₁P₂＝45°，

∴∠P₂P₁B＝90°，即BP₁⊥P₁P₂，∴BP的最小值为BP₁的长，

在等腰直角BCP₁中，CP₁＝BC＝2

∴BP₁＝2√2，∴PB的最小值是2√2，故选：D．

策略3 利用"全等变换"与"三角形三边关系"求线段最值

5．已知：AD＝2，BD＝4，以AB为一边作等边三角形ABC．使C、D两点落在直线AB的两侧．

(1)如图，当∠ADB＝60°时，求AB及CD的长；

(2)当∠ADB变化，且其它条件不变时，求CD的最大值，及相应∠ADB的大小．

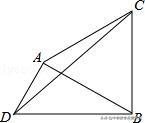
【解析】(1)作AH⊥BD于H，如图，

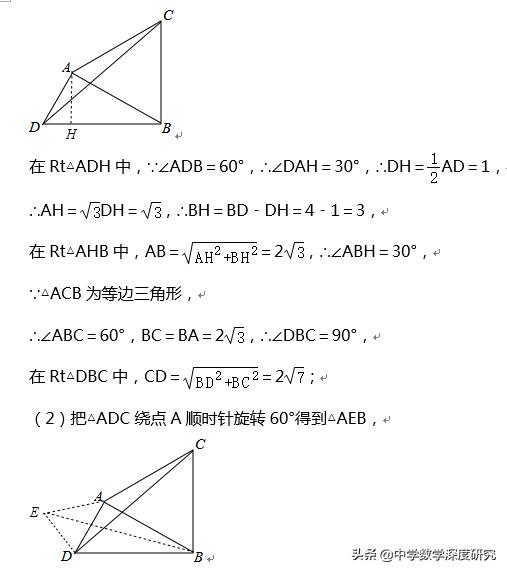
则AE＝AD，BE＝DC，∠EAD＝60°，

∴△ADE为等边三角形，

∴DE＝DA＝2，∠ADE＝60°，

当E点在直线BD上时，BE最大，最大值为2+4＝6，

∴CD的最大值为6，此时∠ADB＝120°．

策略4 利用轴对称变换确定最值

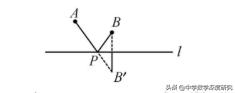
【模型1展示】

A，B是直线l同侧两定点，P是直线l一动点，作点B关于直线l的对称点B´，直线AB交直线1于点P，此时PA+PB最小，等于AB'.)

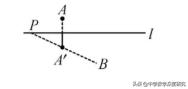
【模型2展示】

A，B是直线l两侧的两个定点，P是直线l一个动点，作点A关于直线l的对称点A'，连接B A'并延长交直线/于点P，此时PB-PA最大，等于A'Ｂ.)

6.(2020•重庆模拟)如图，在矩形ABCD中，AB＝√3，BC＝1，将△ABD沿射线DB平移得到△A'B'D'，连接B′C，D′C，则B'C+D'C的最小值是______．

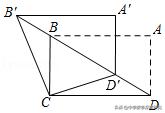
【解答】：∵四边形ABCD是矩形，

7．(2019•陕西)如图，在正方形ABCD中，AB＝8，AC与BD交于点O，N是AO的中点，点M在BC边上，且BM＝6．P为对角线BD上一点，则PM﹣PN的最大值为______．

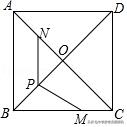
【解答】：如图所示，作以BD为对称轴作N的对称点N'，连接PN'，MN'，

根据轴对称性质可知，PN＝PN'，

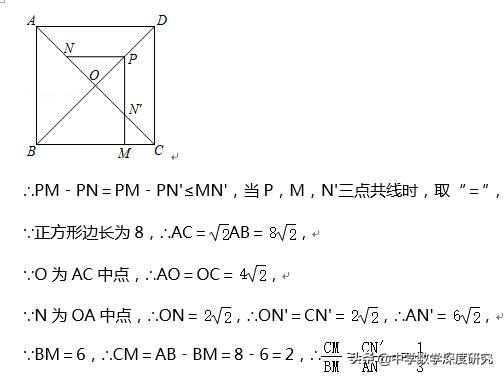
∴PM∥AB∥CD，∠CMN'＝90°，

∵∠N'CM＝45°，∴△N'CM为等腰直角三角形，∴CM＝MN'＝2，

即PM﹣PN的最大值为2，故答案为：2．

策略5 利用"直角三角形中的性质"求线段最值

8．(2019•眉山)如图，在Rt△AOB中，OA＝OB＝4√2．⊙O的半径为2，点P是AB边上的动点，过点P作⊙O的一条切线PQ(点Q为切点)，则线段PQ长的最小值为_______

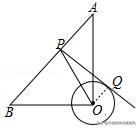
【解答】：连接OQ．∵PQ是⊙O的切线，∴OQ⊥PQ；

9．如图，在⊙O中，直径AB＝8，BC是弦，∠ABC＝30°，点P在BC上，点Q在⊙O上，且OP⊥PQ，当点P在BC上移动时，则PQ长的最大值是(　　)

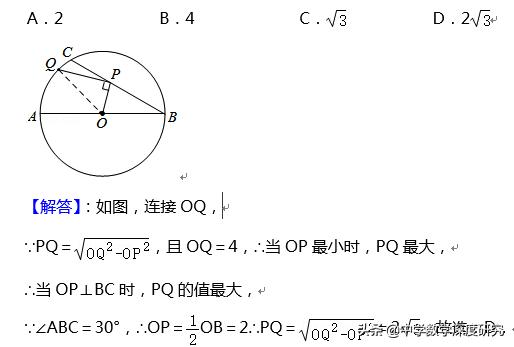
模型6 利用圆的特性确定最值

【模型1展示】

A，B是⊙O上两个动点.当AB经过圈心时，AB最大。

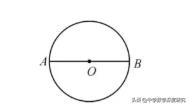
【模型2展示】

A是⊙O外一定点，P是⊙O上一动点，P点运动到点B时，AP最小，P点运动到C点时，AP最大。

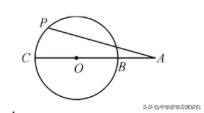
【模型3展示】

AB是⊙O的定弦，P是⊙O上的动点，PC过圆心O，且PC⊥AB时，P点到AB的距离最大。

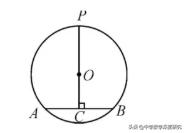
10．(2019•东营)如图，AC是⊙O的弦，AC＝5，点B是⊙O上的一个动点，且∠ABC＝45°，若点M、N分别是AC、BC的中点，则MN的最大值是_______．

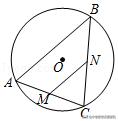
【解答】：∵点M，N分别是BC，AC的中点，

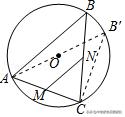
∴MN＝1/2AB，

∴当AB取得最大值时，MN就取得最大值，当AB是直径时，AB最大，

连接AO并延长交⊙O于点B′，连接CB′，

∵AB′是⊙O的直径，∴∠ACB′＝90°．

∵∠ABC＝45°，AC＝5，∴∠AB′C＝45°，

11．(2019•乐山)如图，抛物线y＝1/4x2﹣4与x轴交于A、B两点，P是以点C(0，3)为圆心，2为半径的圆上的动点，Q是线段PA的中点，连结OQ．则线段OQ的最大值是(　　)

模型7 利用建立二次函数模型确定最值

【模型展示】

建立二次函数模型，利用二次函数的增减值，结合自变量的取值范围，确定线段的最值.

12．(2019•包头)如图，在平面直角坐标系中，已知A(﹣3，﹣2)，B(0，﹣2)，C(﹣3，0)，M是线段AB上的一个动点，连接CM，过点M作MN⊥MC交y轴于点N，若点M、N在直线y＝kx+b上，则b的最大值是(　　)

策略8 利用"极值法"求线段取值范围

13．如图，在边长为4的菱形ABCD中，BD＝4，E、F分别是AD、CD上的动点(包含端点)，且AE+CF＝4，连接BE、EF、FB．

(1)试探究BE与BF的数量关系，并证明你的结论；

(2)求EF的最大值与最小值．

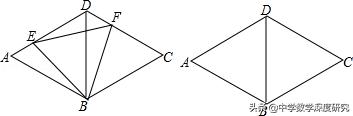
【解答】：(1)BE＝BF，证明如下：

∵四边形ABCD是边长为4的菱形，BD＝4，

∴△ABD、△CBD都是边长为4的正三角形，

∵AE+CF＝4，∴CF＝4﹣AE＝AD﹣AE＝DE，

又∵BD＝BC＝4，∠BDE＝∠C＝60°，

易证明△BDE≌△BCF(SAS)，∴BE＝BF；

(2)∵△BDE≌△BCF，∴∠EBD＝∠FBC，

∴∠EBD+∠DBF＝∠FBC+∠DBF，∴∠EBF＝∠DBC＝60°，

又∵BE＝BF，∴△BEF是正三角形，∴EF＝BE＝BF，

当动点E运动到点D或点A时，BE的最大值为4，

当BE⊥AD，即E为AD的中点时，BE的最小值为2√3，

∵EF＝BE，∴EF的最大值为4，最小值为2√3．

变式．在边长为a的菱形ABCD中，∠DAB＝60°，E是AD上异于A，D两点的动点，F是CD上的动点，满足AE+CF＝a

(1)求证：△BDE≌△BCF；

(2)证明：不论E、F怎样移动，△BEF总是等边三角形．

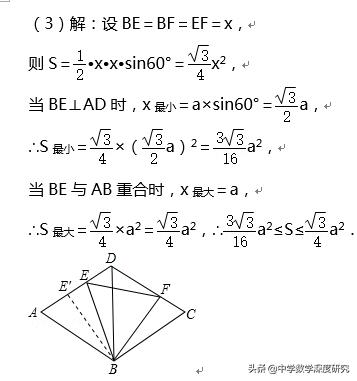
(3)设△BEF的面积为S，求S的取值范围．

【解答】(1)证明：∵四边形ABCD是菱形，∴AB＝AD．

又∵∠DAB＝60°，∴△ABD是等边三角形，∴BD＝AD，

∵菱形ABCD的边长为a，∴BD＝a，

∴△ABD和△BCD都为正三角形，

∴∠BDE＝∠BCF＝60°，BD＝BC，

∵AE+DE＝AD＝a，而AE+CF＝a，∴DE＝CF．

易证△BDE≌△BCF(SAS)；

(2)解：△BEF为正三角形．

理由：∵△BDE≌△BCF，∴∠DBE＝∠CBF，BE＝BF，

∵∠DBC＝∠DBF+∠CBF＝60°，∴∠DBF+∠DBE＝60°即∠EBF＝60°，

∴△BEF为正三角形；

总之，线段的最值问题(或线段取值范围)的解题关键就是要结合题意，借助相关的概念，图形性质，将最值问题转化相应数学模型进行分析与突破。

区分两点间距离与点到直线距离，在于看几个线段和的两个端点：(1)如果两个端点都是定点，则是两个点距离；(2)如果两个端点是一个动点一个定点则是点到直线的距离。区分三边关系与距离最短，在于从形式上看是一条线段的最值还是两三条线段和的最值，一条线段则是通过三边关系，两三条线段和则是两点间距离或点到直线距离。