manacher java_Manacher 算法

给定一个字符串，求出其最长回文子串。例如：s="abcd"，最长回文长度为 1；

s="ababa"，最长回文长度为 5；

s="abccb"，最长回文长度为 4，即 bccb。

以上问题的传统思路大概是，遍历每一个字符，以该字符为中心向两边查找。其时间复杂度为 $O(n^2)$，效率很差。

1975 年，一个叫 Manacher 的人发明了一个算法，Manacher 算法(中文名：马拉车算法)，该算法可以把时间复杂度提升到 $O(n)$。下面来看看马拉车算法是如何工作的。

算法过程分析

由于回文分为偶回文(比如 bccb)和奇回文(比如 bcacb)，而在处理奇偶问题上会比较繁琐，所以这里我们使用一个技巧，具体做法是：在字符串首尾及每个字符间都插入一个 "#"，这样可以使得原先的奇偶回文都变为奇回文；

接着再在首尾两端各插入 "$" 和 "^"，这样中心扩展寻找回文的时候会自动退出循环，不需每次判断是否越界，可参见下面代码。

上述新插入的三个字符，即 "#"、 "$" 和 "^"，必须各异，且不可以与原字符串中的字符相同。

举个例子：s="abbahopxpo"，转换为 s_new="$#a#b#b#a#h#o#p#x#p#o#^"。如此，s 里起初有一个偶回文 abba 和一个奇回文 opxpo，被转换为 #a#b#b#a# 和 #o#p#x#p#o#，长度都转换成了奇数。

定义一个辅助数组 int p[]，其中 p[i] 表示以 i 为中心的最长回文的半径，例如：i012345678910111213141516171819202122s_new[i]$#a#b#b#a#h#o#p#x#p#o#^

p[i]11212521212121216121211

可以看出，p[i] - 1 正好是原字符串中最长回文串的长度。

接下来的重点就是求解 p 数组，如下图：

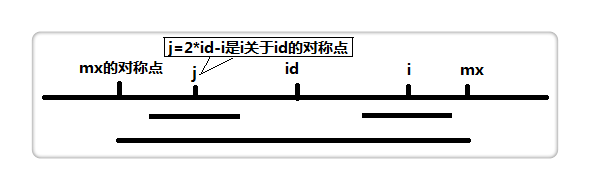
设置两个变量，mx 和 id 。mx 代表以 id 为中心的最长回文的右边界，也就是 mx = id + p[id]。

假设我们现在求 p[i]，也就是以 i 为中心的最长回文半径，如果 i < mx，如上图，那么：if (i < mx)

p[i] = min(p[2 * id - i], mx - i);

2 * id - i 为 i 关于 id 的对称点，即上图的 j 点，而 p[j]表示以 j 为中心的最长回文半径，因此我们可以利用 p[j] 来加快查找。

代码#include

#include

#include

using namespace std;

char s[1000];

char s_new[2000];

int p[2000];

int Init()

{

int len = strlen(s);

s_new[0] = '$';

s_new[1] = '#';

int j = 2;

for (int i = 0; i < len; i++)

{

s_new[j++] = s[i];

s_new[j++] = '#';

}

s_new[j++] = '^'; // 别忘了哦

s_new[j] = '\0'; // 这是一个好习惯

return j; // 返回 s_new 的长度

}

int Manacher()

{

int len = Init(); // 取得新字符串长度并完成向 s_new 的转换

int max_len = -1; // 最长回文长度

int id;

int mx = 0;

for (int i = 1; i < len; i++)

{

if (i < mx)

p[i] = min(p[2 * id - i], mx - i); // 需搞清楚上面那张图含义，mx 和 2*id-i 的含义

else

p[i] = 1;

while (s_new[i - p[i]] == s_new[i + p[i]]) // 不需边界判断，因为左有 $，右有 ^

p[i]++;

// 我们每走一步 i，都要和 mx 比较，我们希望 mx 尽可能的远，

// 这样才能更有机会执行 if (i < mx)这句代码，从而提高效率

if (mx < i + p[i])

{

id = i;

mx = i + p[i];

}

max_len = max(max_len, p[i] - 1);

}

return max_len;

}

int main()

{

while (printf("请输入字符串："))

{

scanf("%s", s);

printf("最长回文长度为 %d\n\n", Manacher());

}

return 0;

}

测试如下：请输入字符串：abbahopxpo

最长回文长度为 5

请输入字符串：a

最长回文长度为 1

请输入字符串：aa

最长回文长度为 2

请输入字符串：abax

最长回文长度为 3

算法复杂度分析

文章开头已经提及，Manacher 算法为线性算法，即使最差情况下其时间复杂度亦为 $O(n)$，在进行证明之前，我们还需要更加深入地理解上述算法过程。

根据回文的性质，p[i] 的值基于以下三种情况得出：

(1)：j 的回文串有一部分在 id 的之外，如下图：

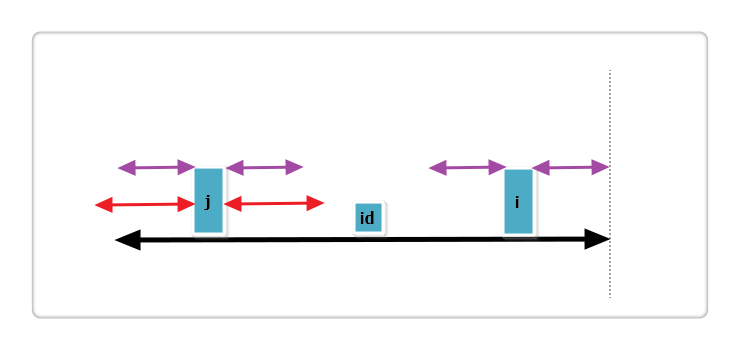
上图中，黑线为 id 的回文，i 与 j 关于 id 对称，红线为 j 的回文。那么根据代码此时 p[i] = mx - i，即紫线。那么 p[i] 还可以更大么？答案是不可能！见下图：

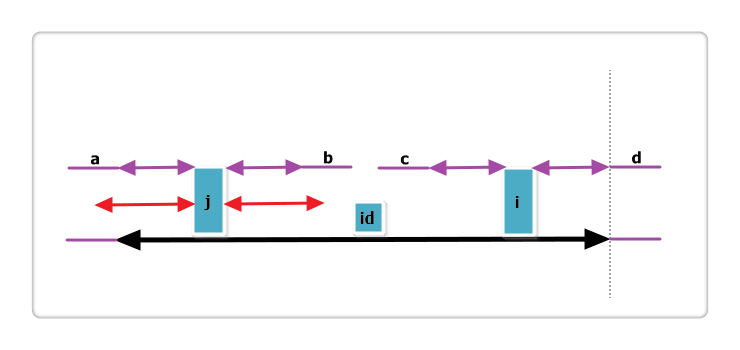
假设右侧新增的紫色部分是 p[i] 可以增加的部分，那么根据回文的性质，a 等于 d ，也就是说 id 的回文不仅仅是黑线，而是黑线+两条紫线，矛盾，所以假设不成立，故 p[i] = mx - i，不可以再增加一分。

(2)：j 回文串全部在 id 的内部，如下图：

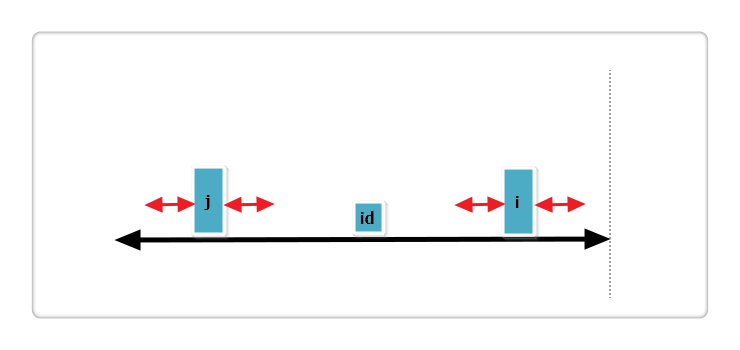
根据代码，此时 p[i] = p[j]，那么 p[i] 还可以更大么？答案亦是不可能！见下图：

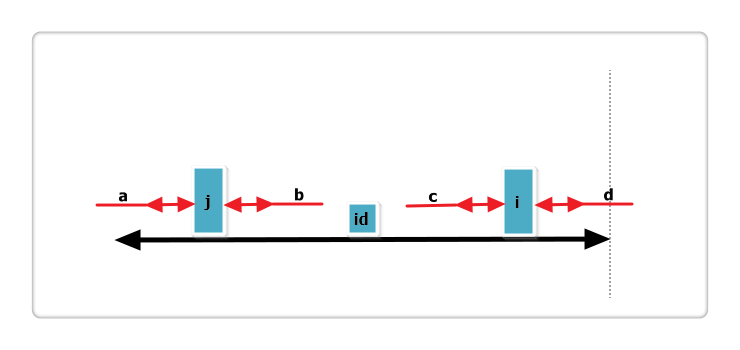
假设右侧新增的红色部分是 p[i] 可以增加的部分，那么根据回文的性质，a 等于 b ，也就是说 j 的回文应该再加上 a 和 b ，矛盾，所以假设不成立，故 p[i] = p[j]，也不可以再增加一分。

(3)：j 回文串左端正好与 id 的回文串左端重合，见下图：

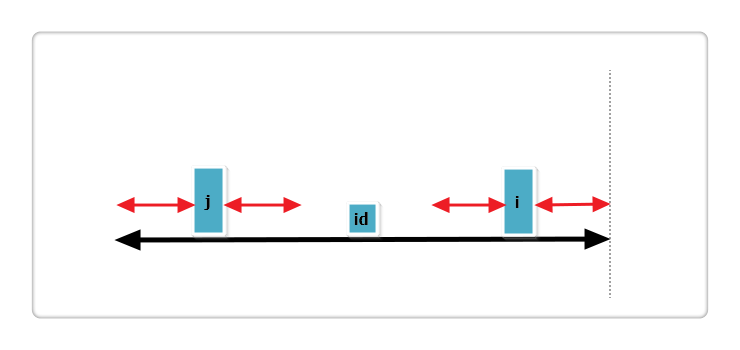
根据代码，此时 p[i] = p[j] 或 p[i] = mx - i，并且 p[i] 还可以继续增加，所以需要while (s_new[i - p[i]] == s_new[i + p[i]])

p[i]++;

根据(1)(2)(3)，很容易推出 Manacher 算法的最坏情况，即为字符串内全是相同字符的时候。在这里我们重点研究 Manacher() 中的 for 语句，推算发现 for 语句内平均访问每个字符 5 次，即时间复杂度为：$T_{worst}(n)=O(n)$。

同理，我们也很容易知道最佳情况下的时间复杂度，即字符串内字符各不相同的时候。推算得平均访问每个字符 4 次，即时间复杂度为：$T_{best}(n)=O(n)$。

综上，Manacher 算法的时间复杂度为 $O(n)$。