均值极差图控制上下限_均值控制图的三西格玛控制限是如何得出的？

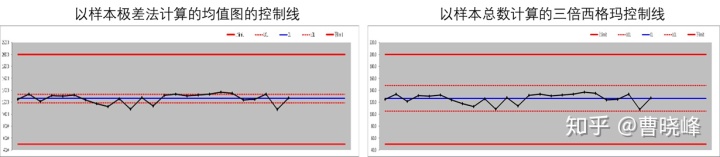
有学员提问：应客户要求，加了好几处SPC. 但发现一个问题，用历史数据计算控制线时，若使用SPC手册定义的Xbar—R 公式，控制线特别窄，窄到80%的点超出控制。但是，如果使用25组每组5个样本的总数据计算标准差，再以三倍的标准差为控制线作图，则显示控制图比较好。

1）为什么两种算法得出的控制线差异如此巨大？

2）可不可以使用样本总数计算的三倍标准差来作为控制线？为什么？

解答如下：

先说结论：不可以使用样本总数计算的三倍标准差来作为控制限。

再说原因。

我们不断地从过程中取样，所取的样越多，样本的均值就越接近于总体均值，所以，我们可以得出一个假设，样本组的均值是围绕着总体均值而上下波动的，并且我们以所抽取的各个样本组的均值的均值来估计该过程的总体均值。

随机抽取的每个样本组，其组内的变异都是不一样的，该变异的大小可以使用多种方法来估计，一种是利用样本组的极差法来估计（

），另一种是利用样本组的标准差法来估计（