二重积分，三重积分

• 个人重点
  1.★画图，穿线，定积分
  2.几何意义
  3.性质(线面对称，奇偶性，中值定理)
  4.计算 (直角坐标，极坐标，柱坐标，球坐标)
  5.综合能力(累次积分交换顺序，累次积分求导，累次积分证明不等式....)

---

几何意义

• 极坐标下的二重积分

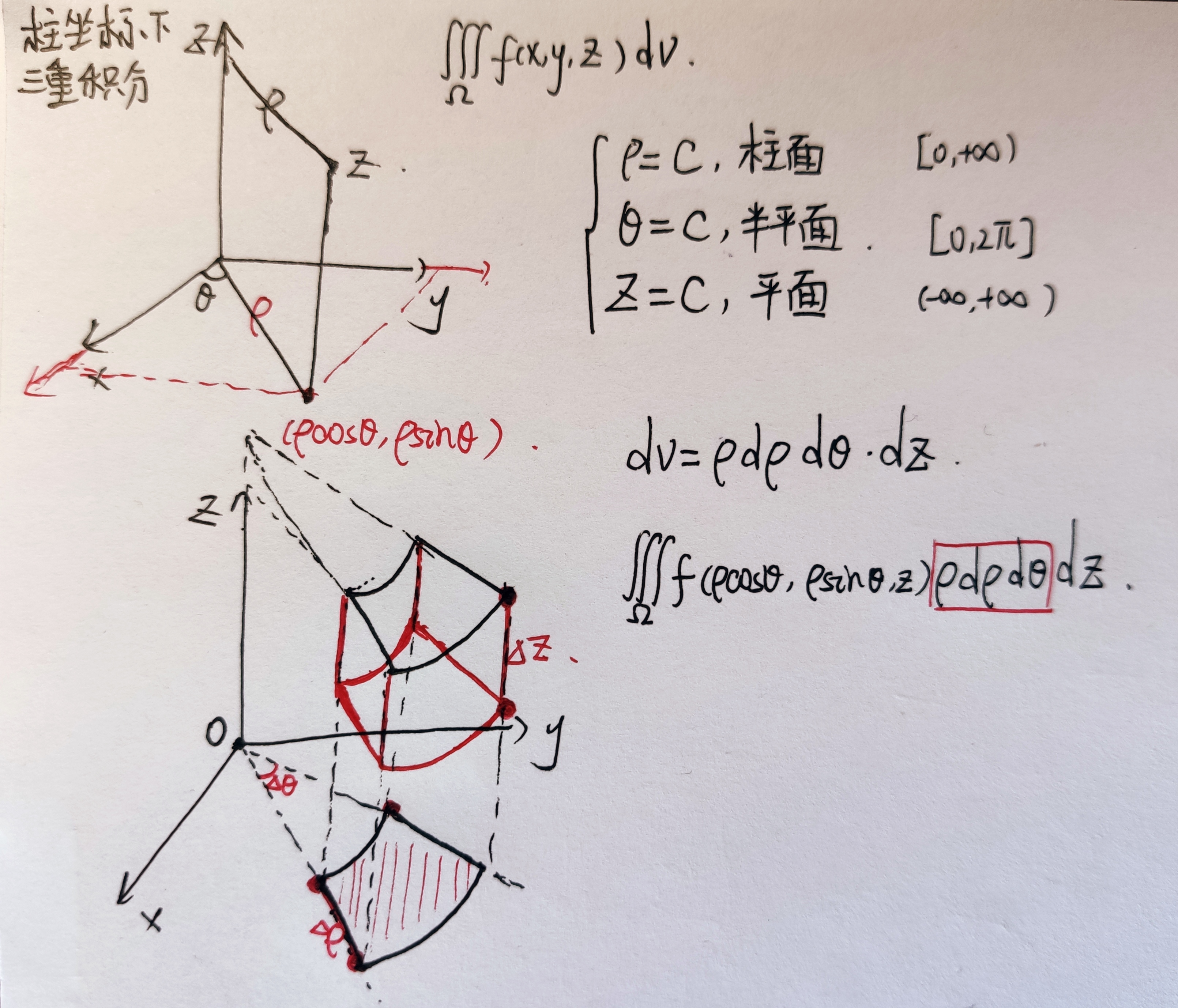
• 柱坐标下的三重积分·

• 球坐标下的三重积分

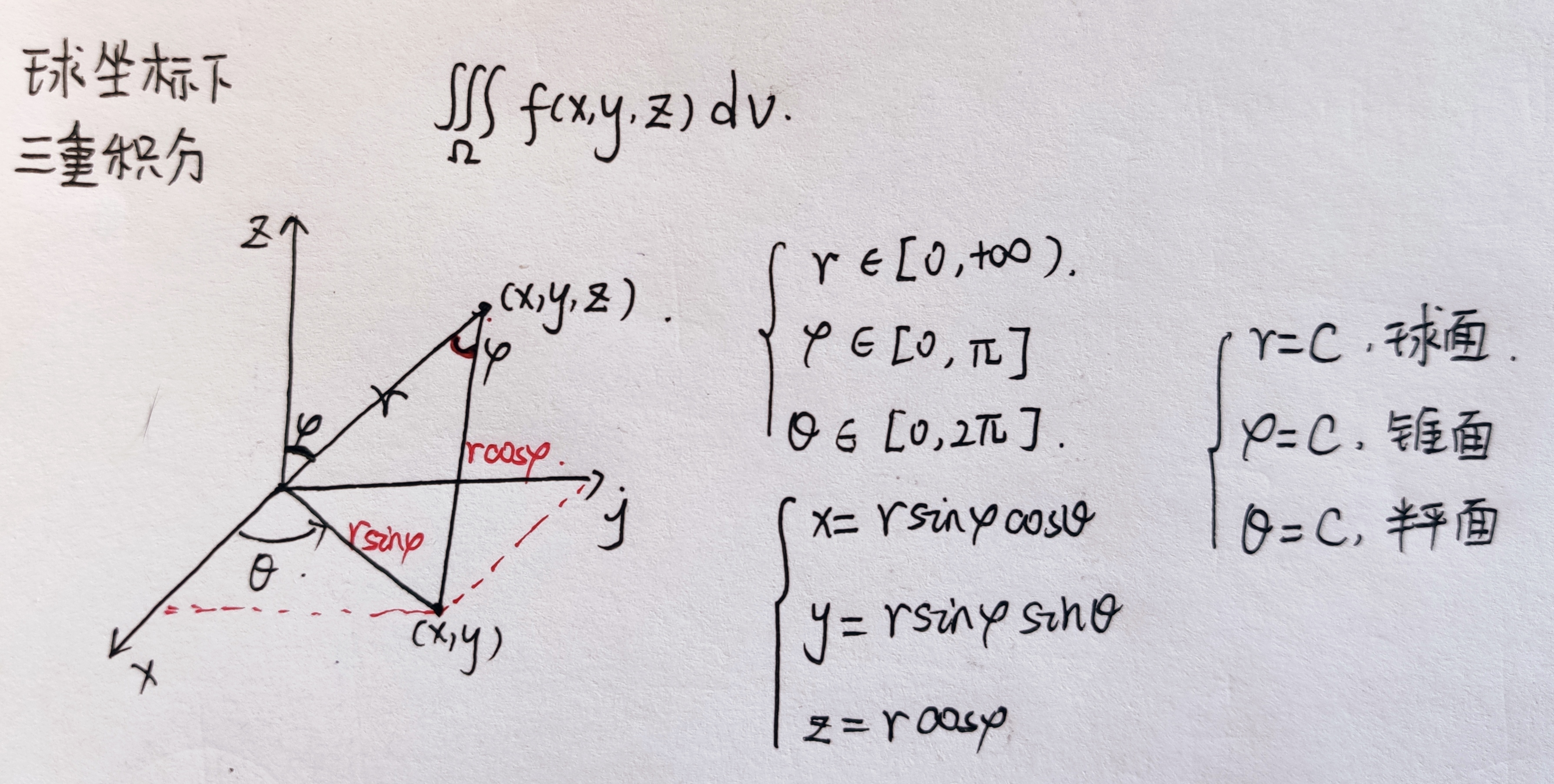
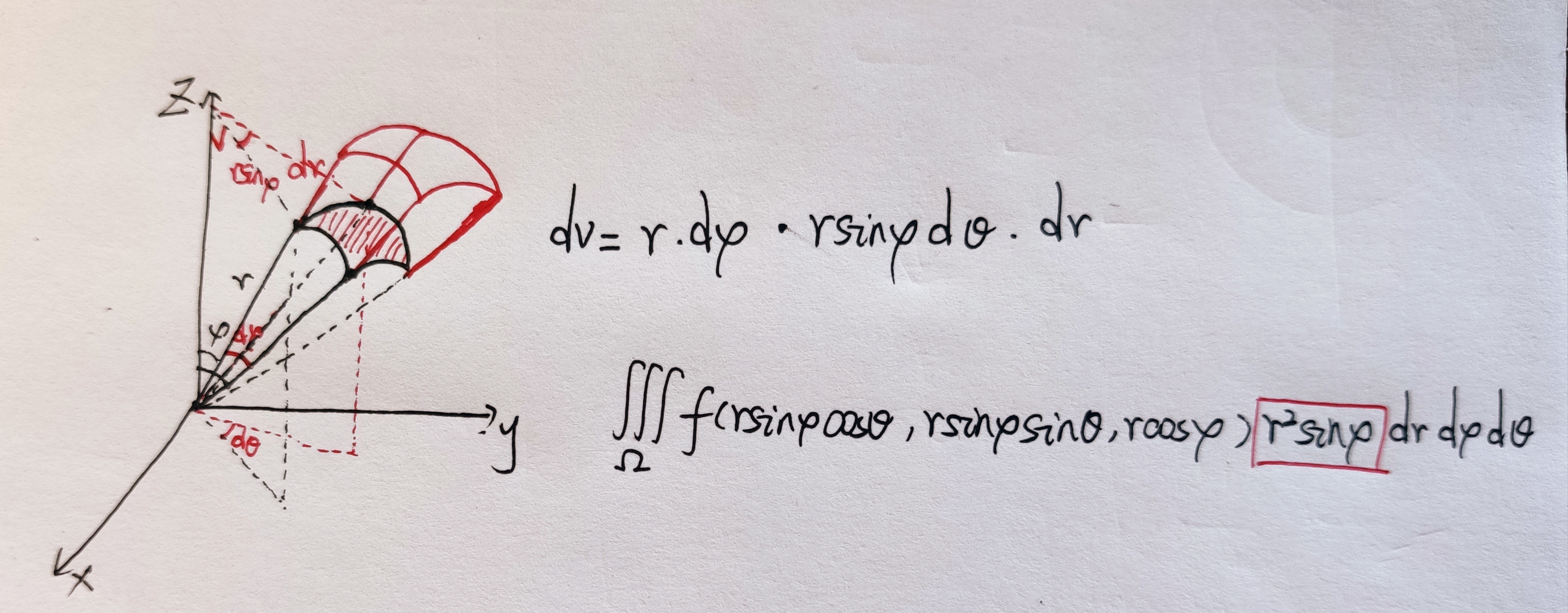
//另外两个直角坐标

---

奇偶性对称性

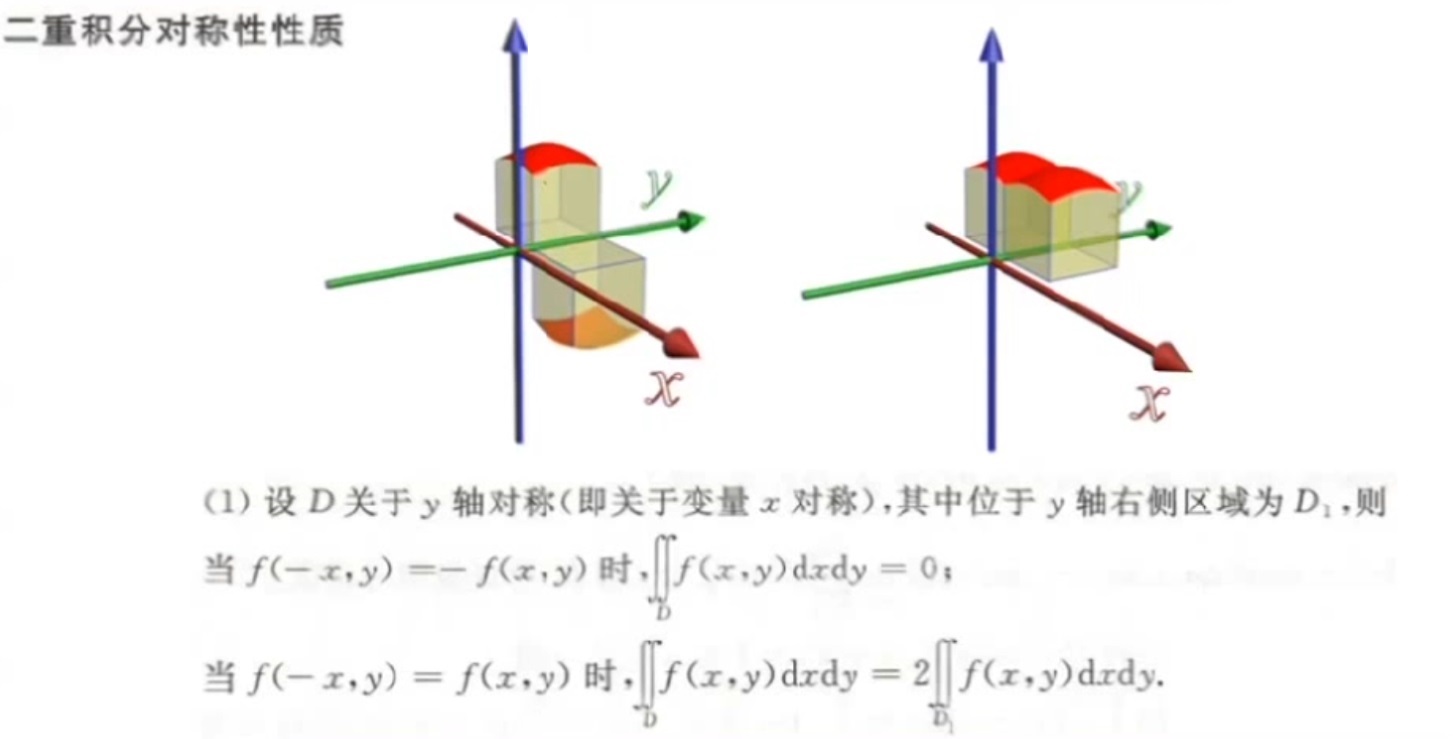
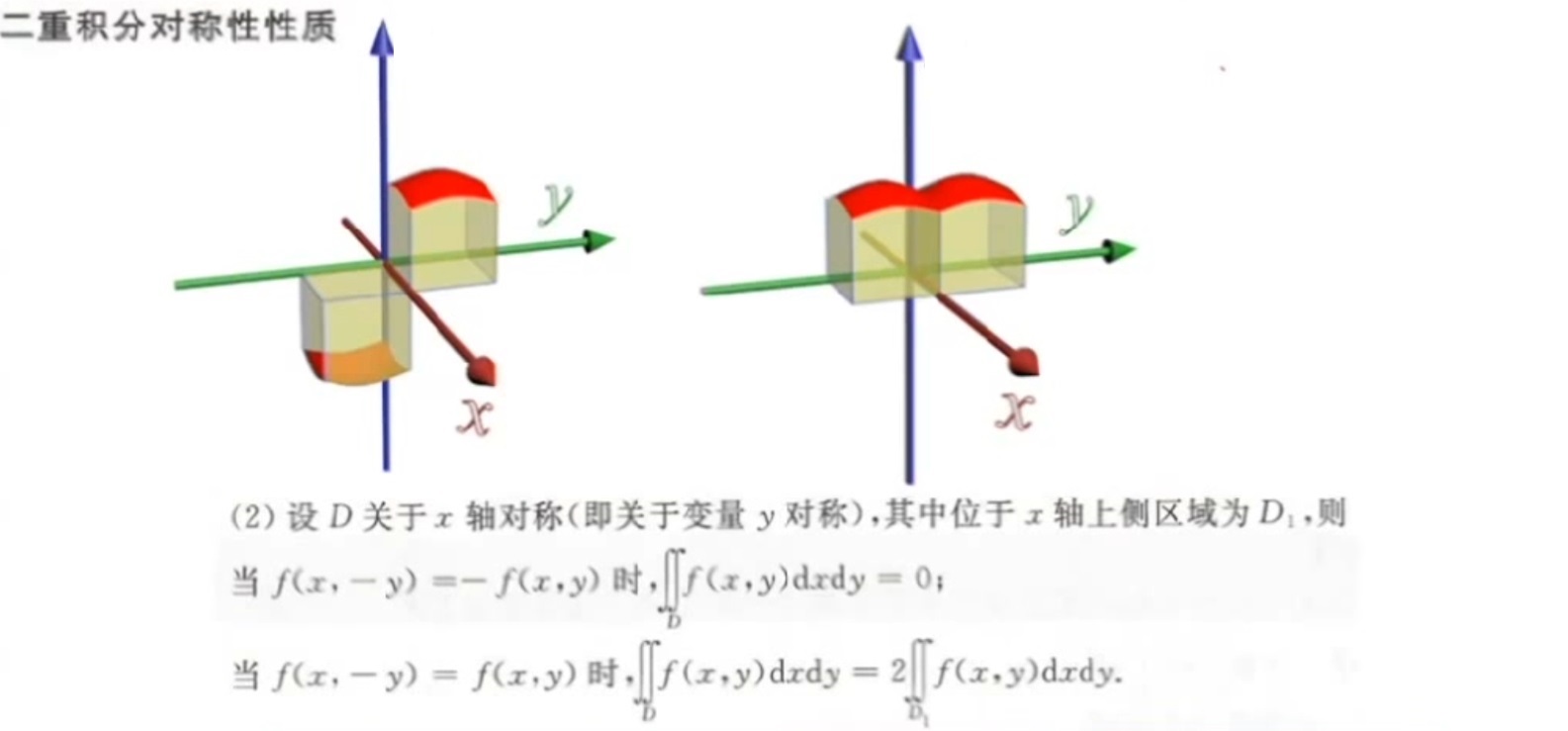
• 积分域关于某直线，某面对称

三重积分类似，换成关于面对称

---

---

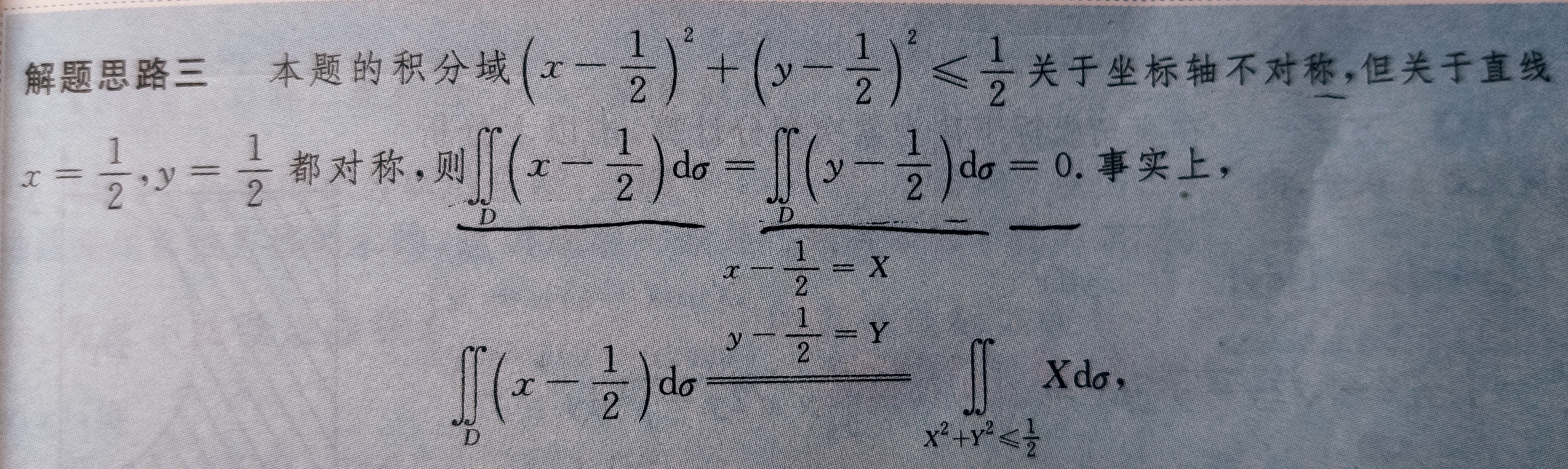
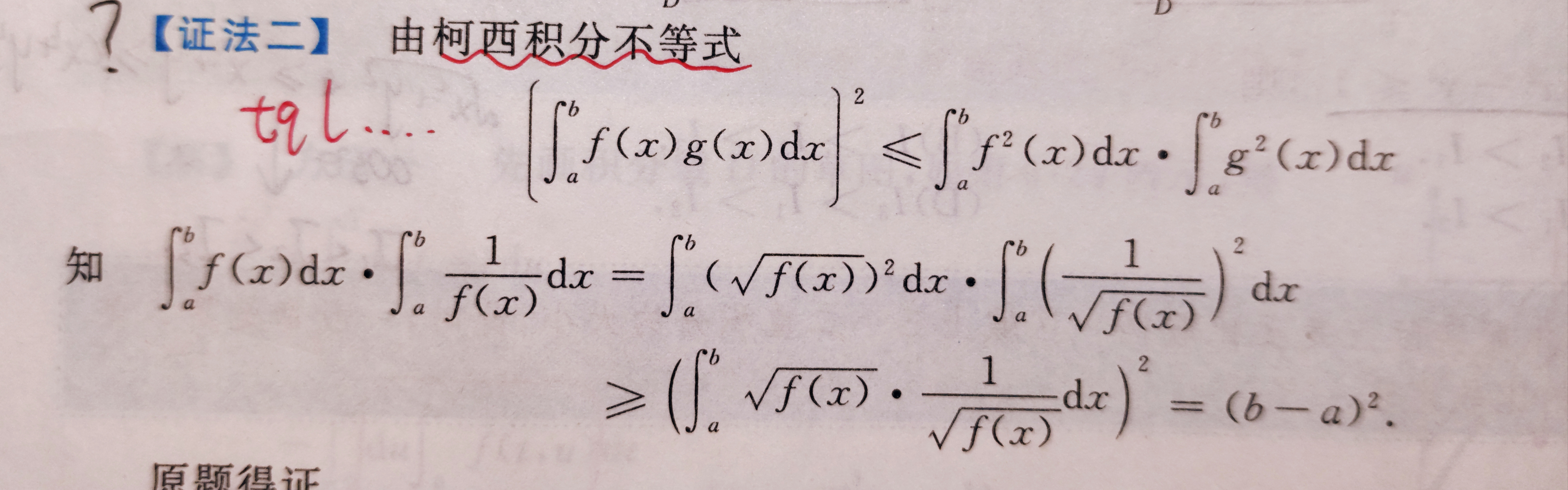
补充知识点

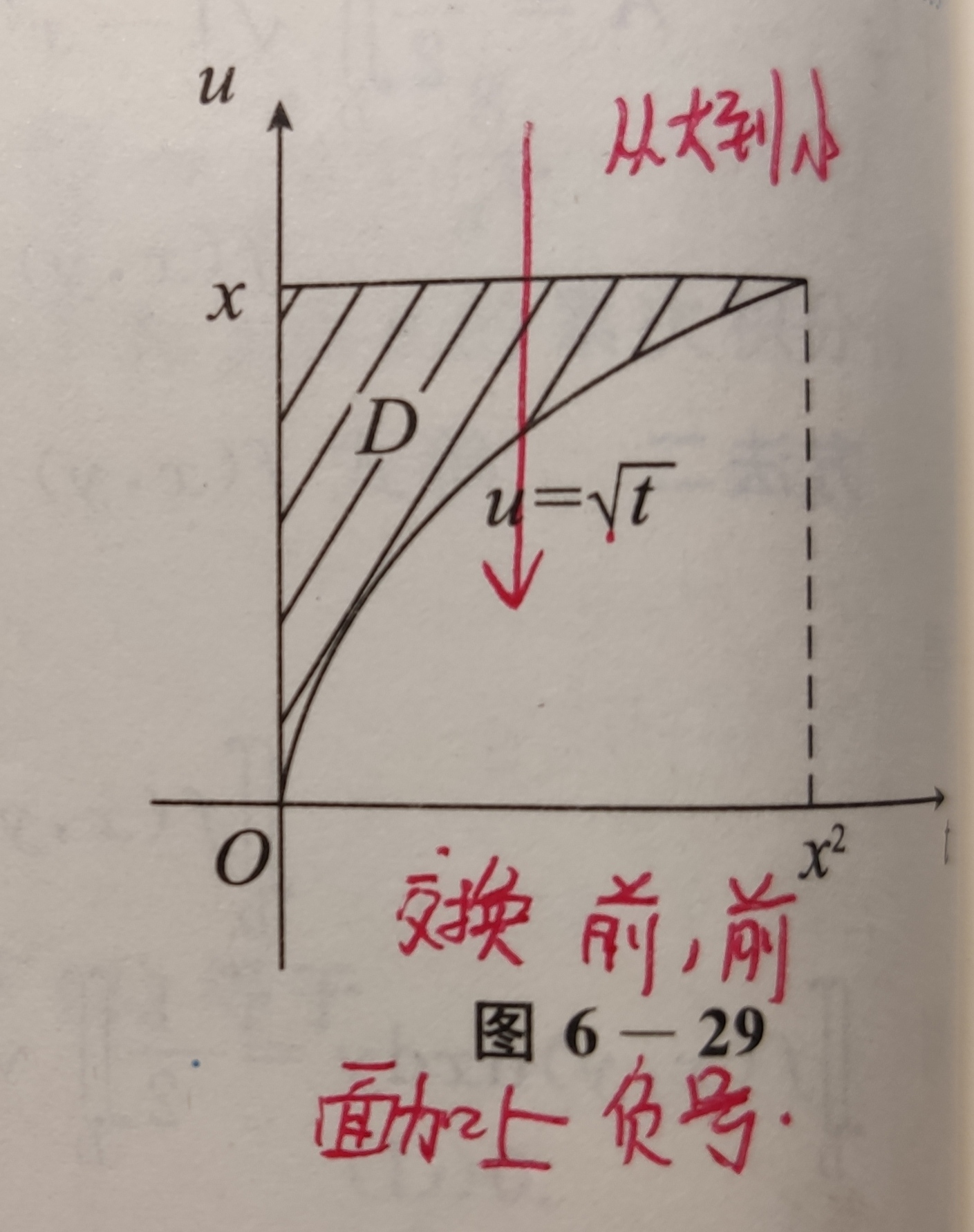
• 前挪大法，三重积分同理

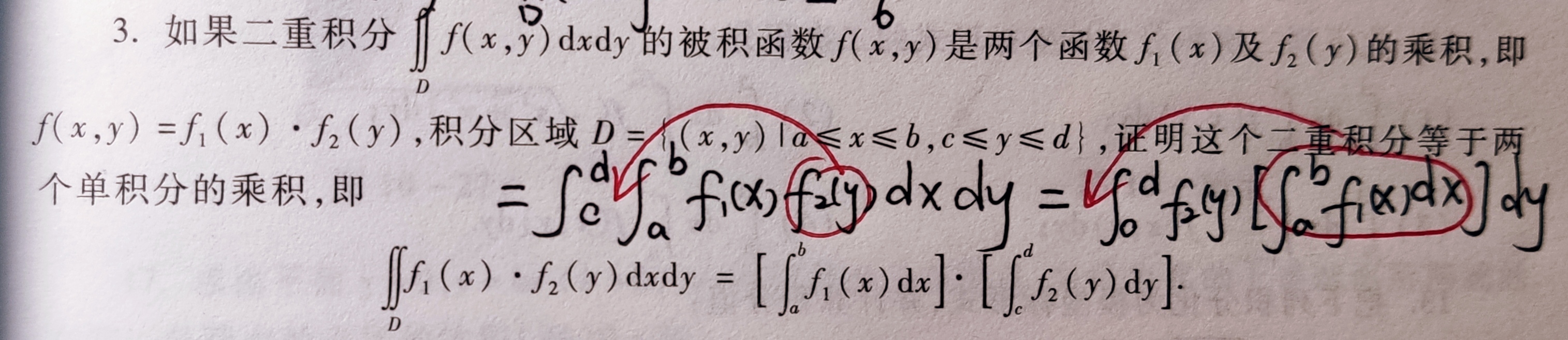
• 证明一个重要积分

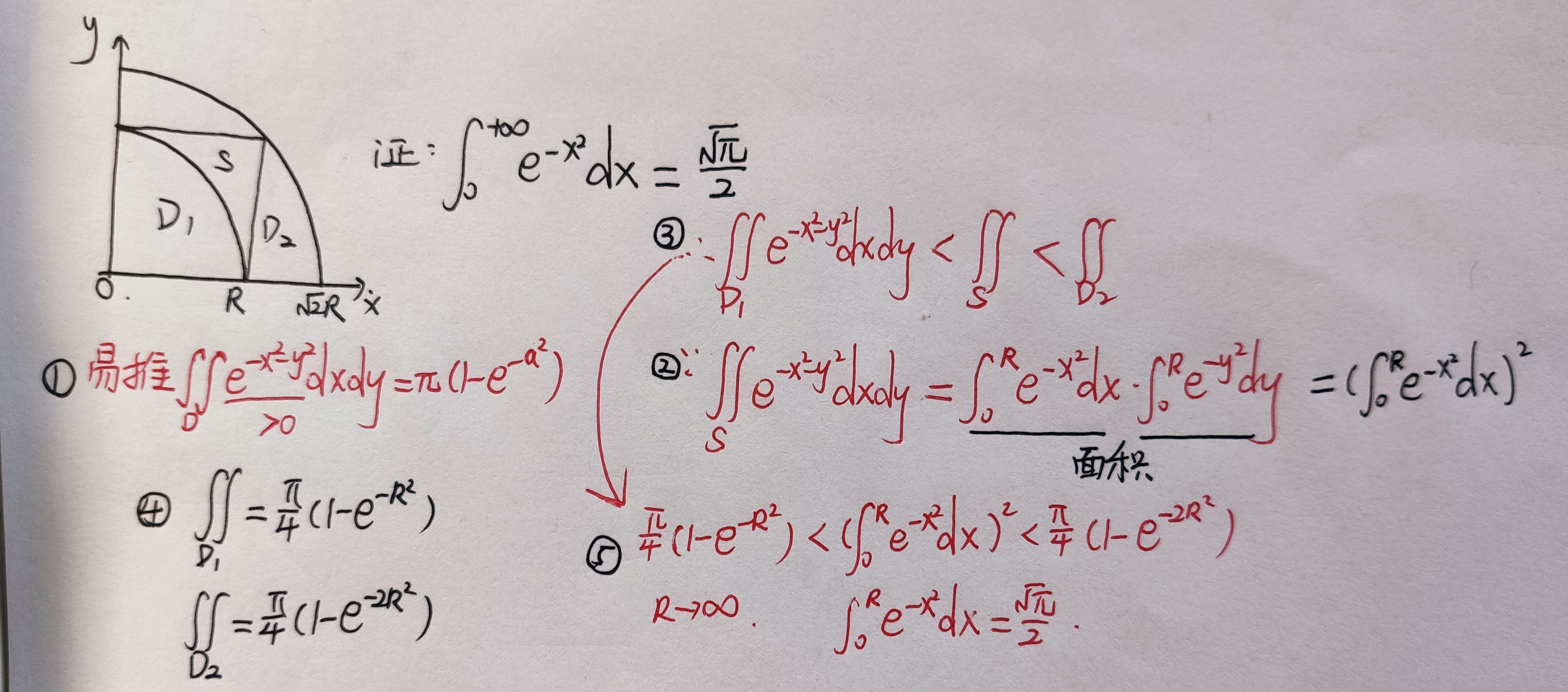
• 穿线的方向

• 形心

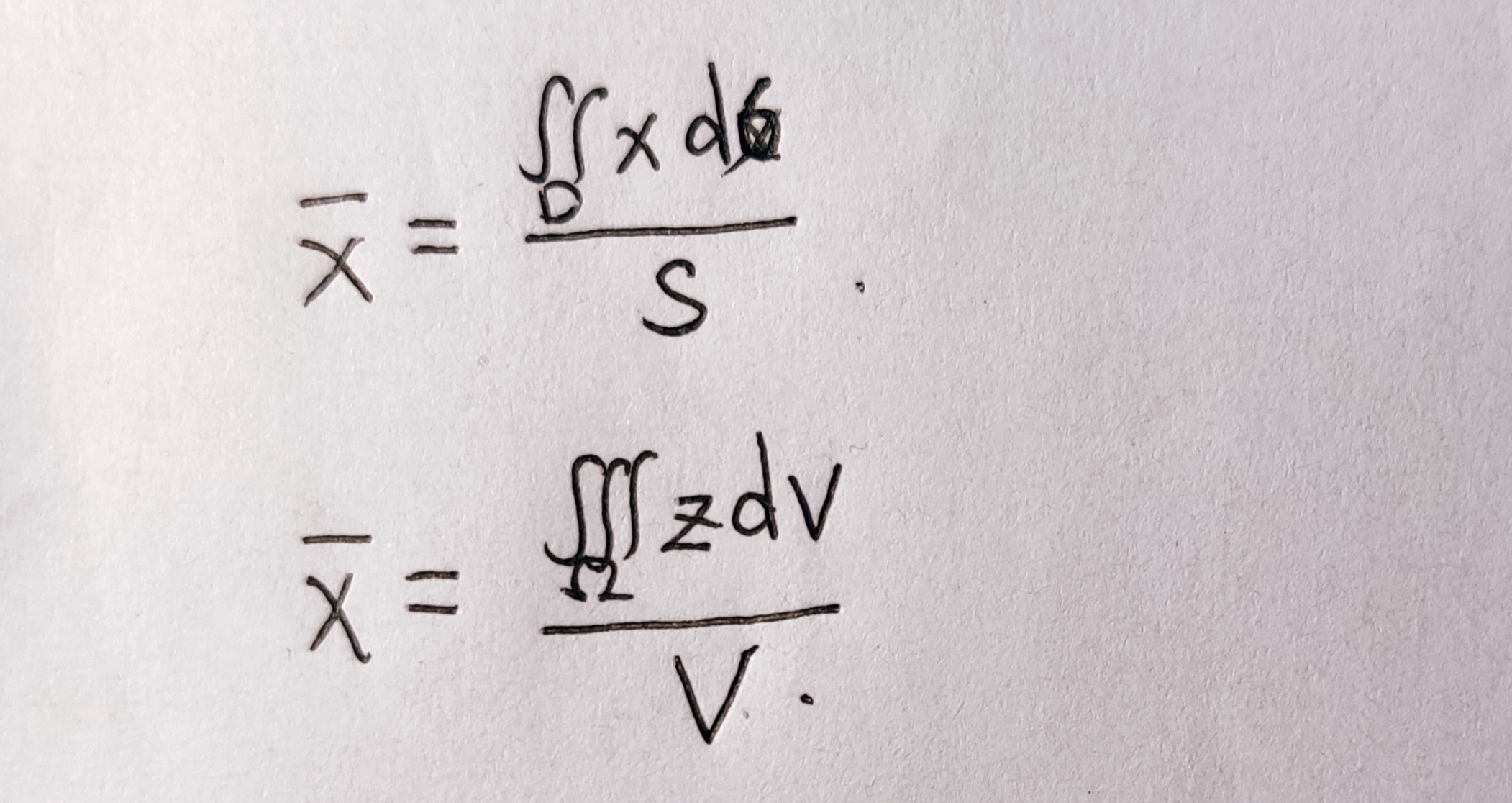
• 还原

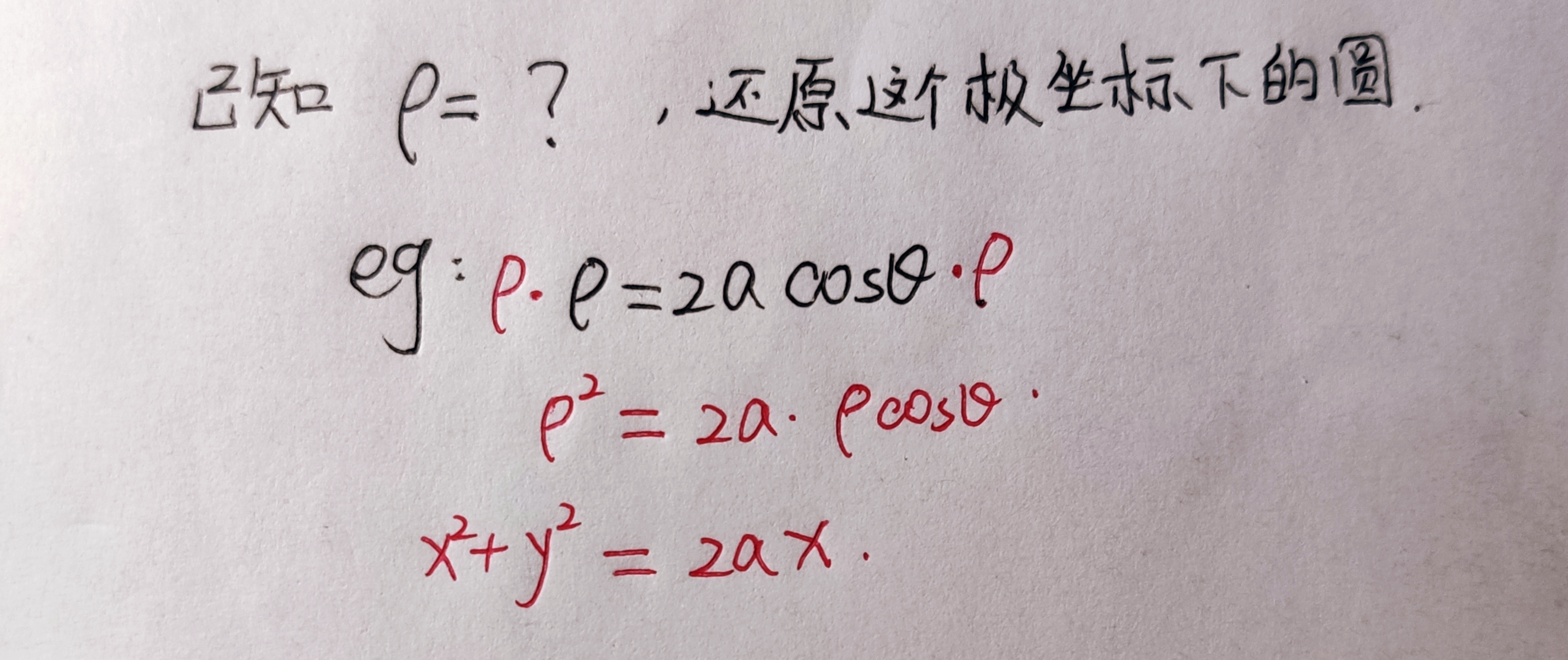
• 极坐标中的平移处理偏心⚪

---

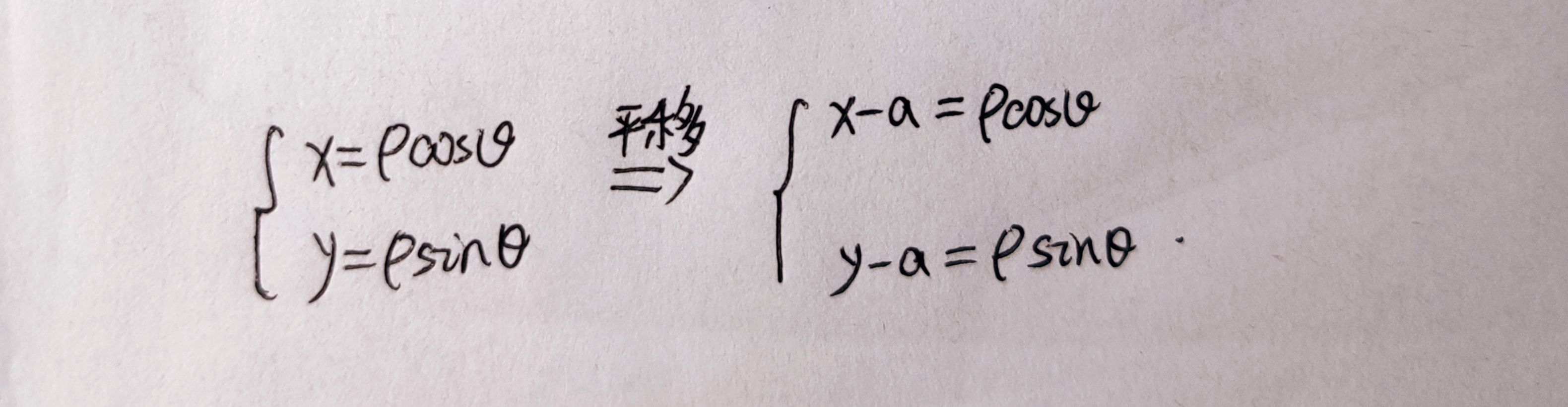
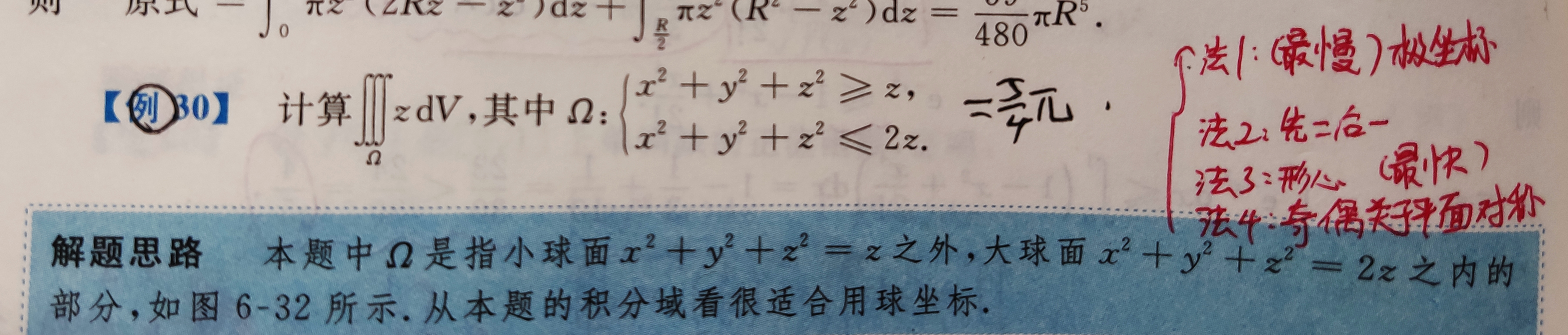
积分中值定理

喜欢和极限一起来考

---

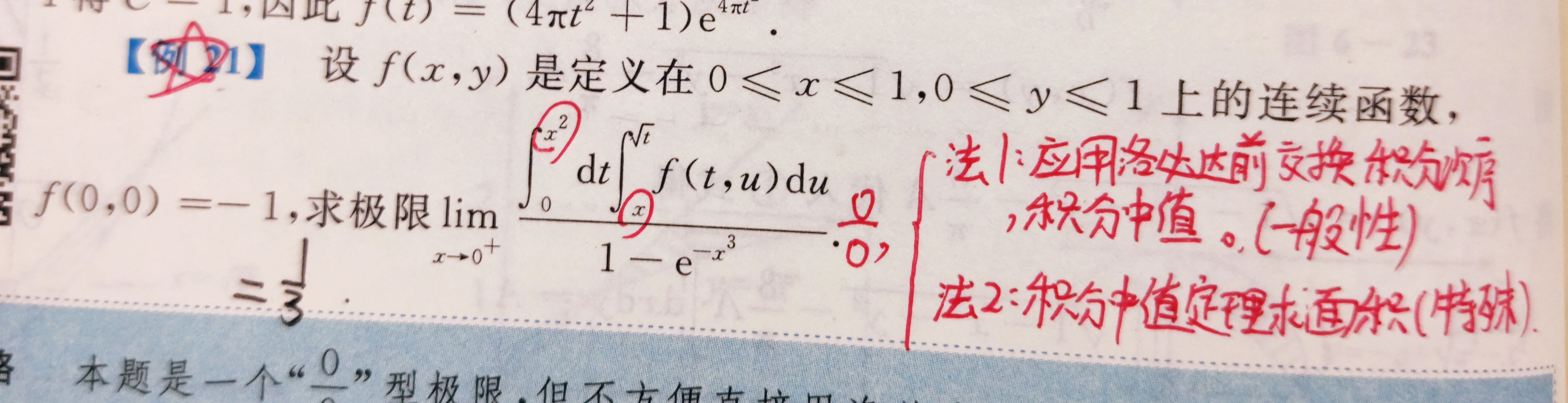
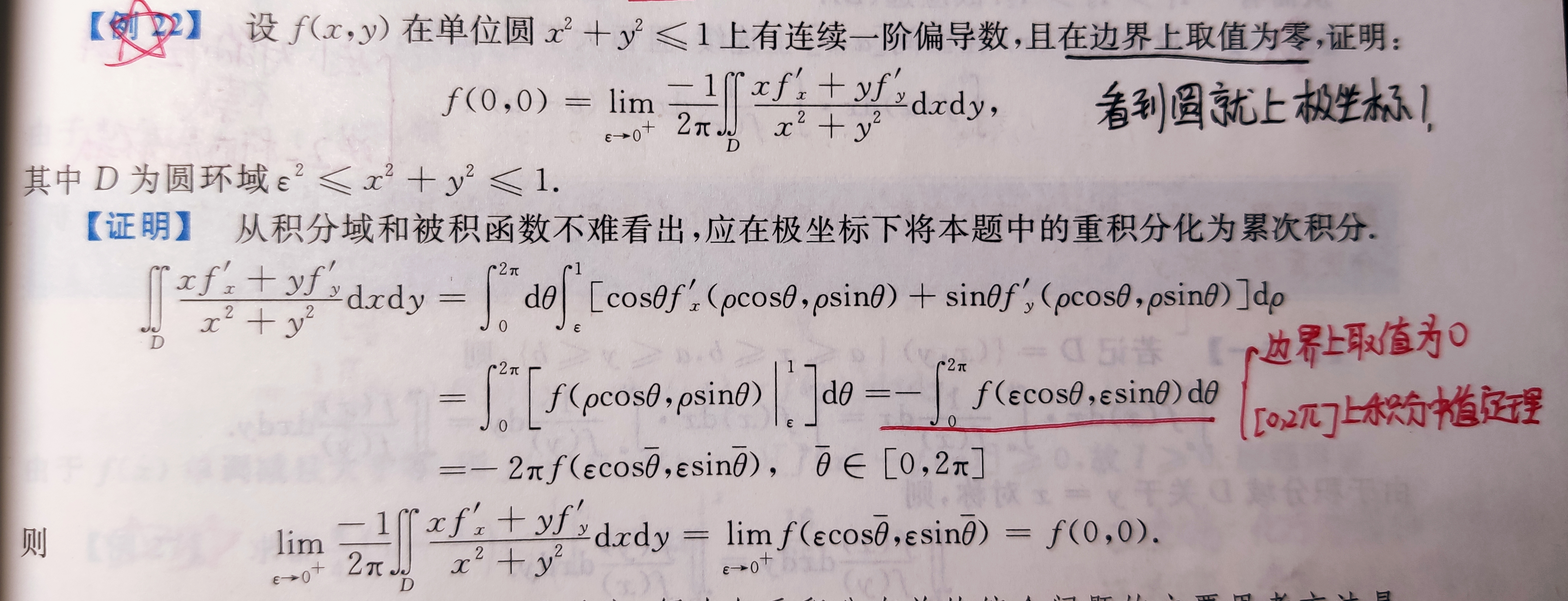
累次积分顺序

具体模型具体分析

---

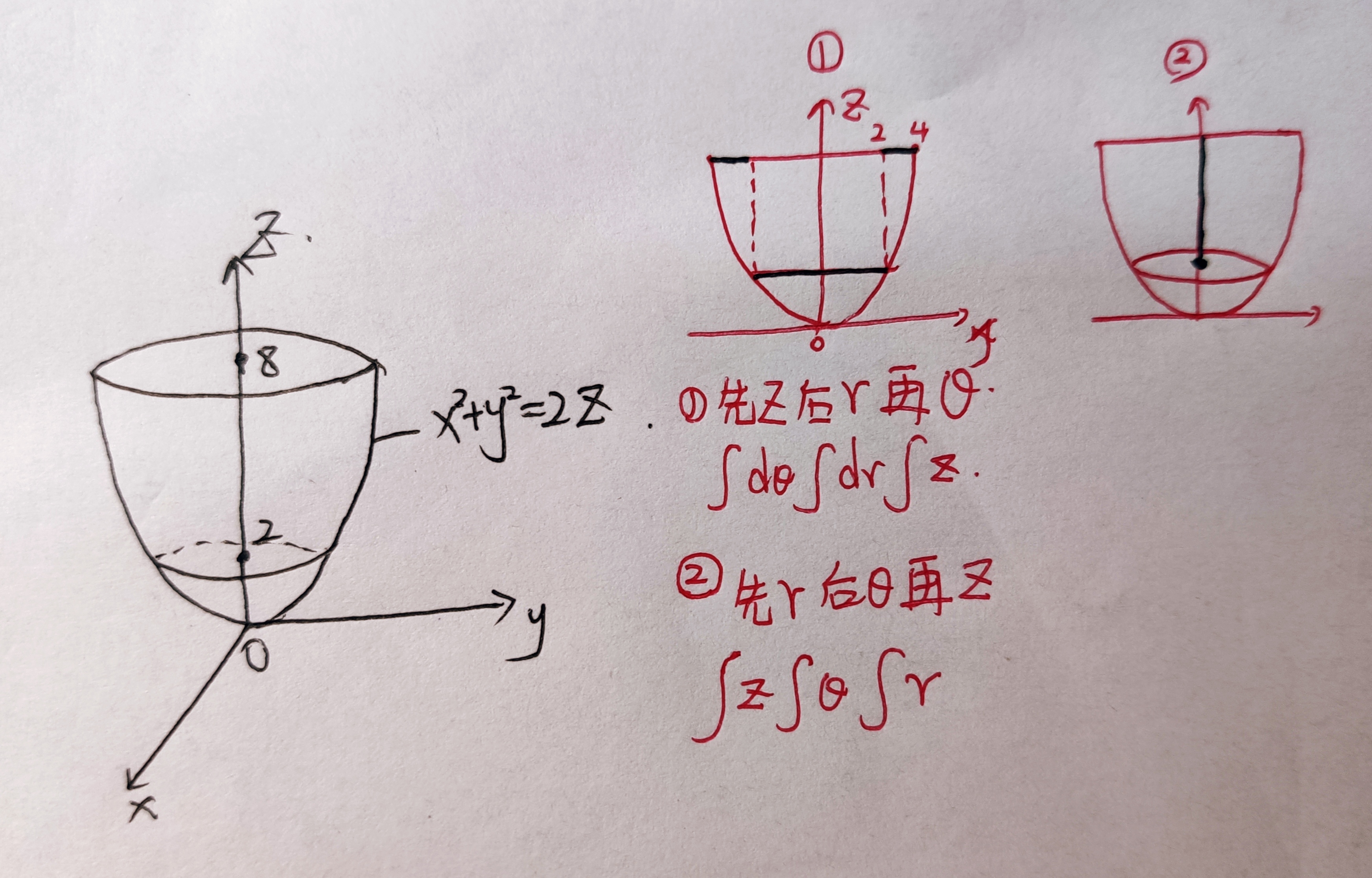
累次积分交换

两个平方二重极坐标or三重柱坐标，三个平方球坐标

---

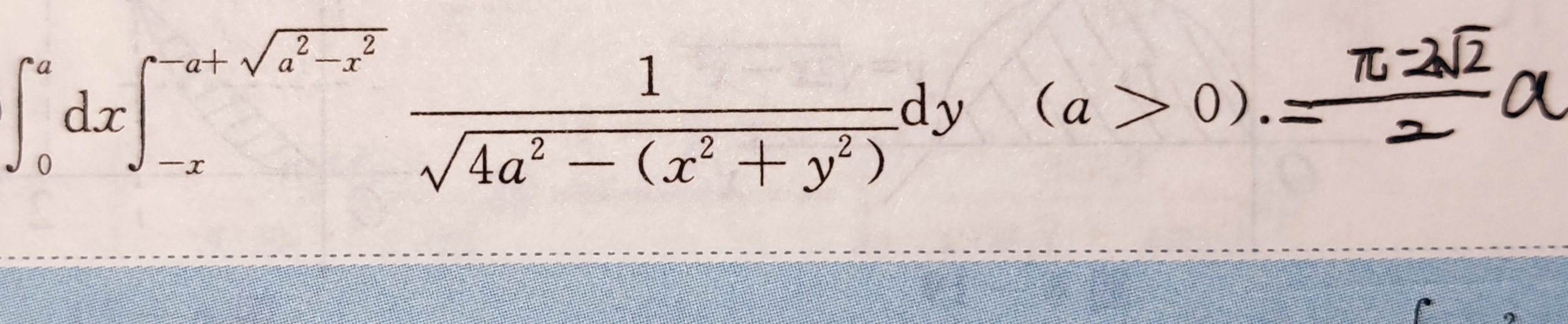
累次积分交换顺序

二重积分直接画空间图即可

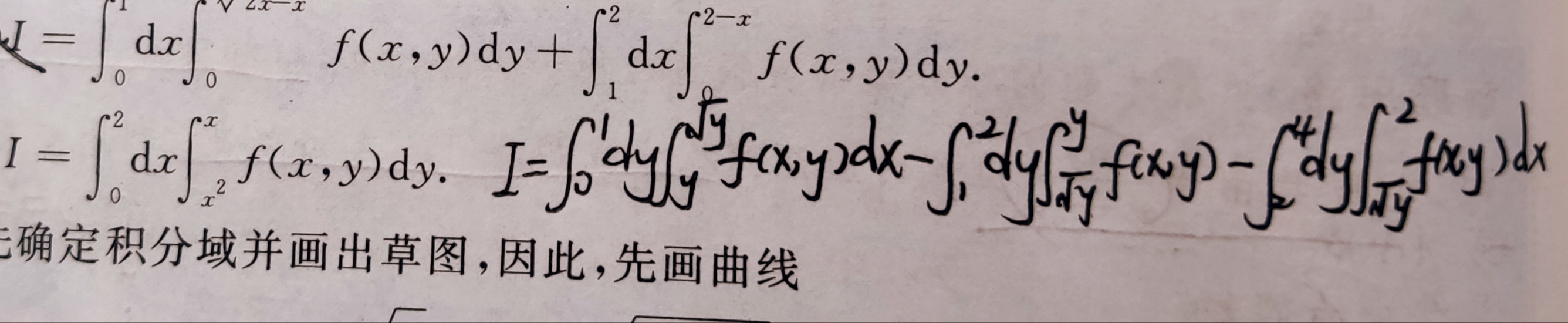
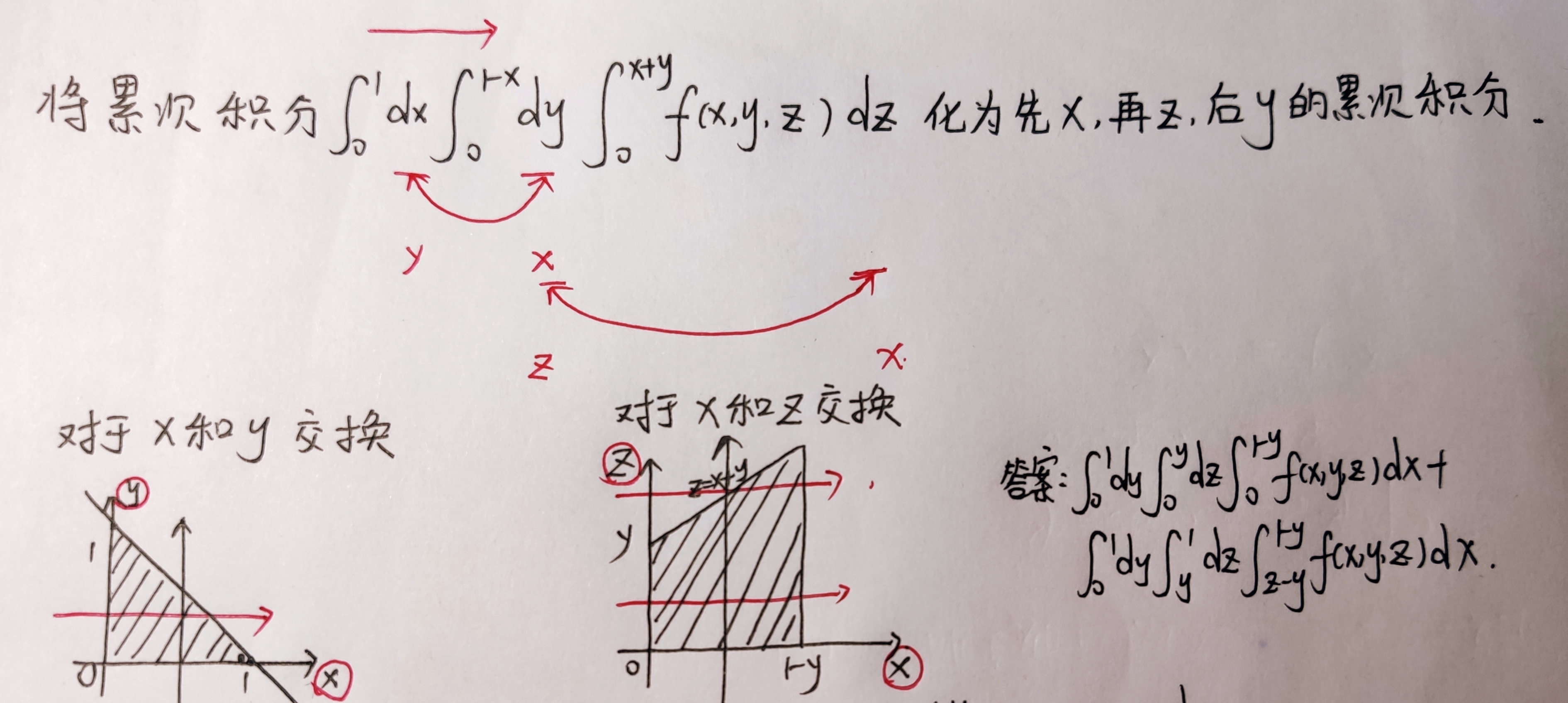
三重积分图比较抽象，换到二维投影

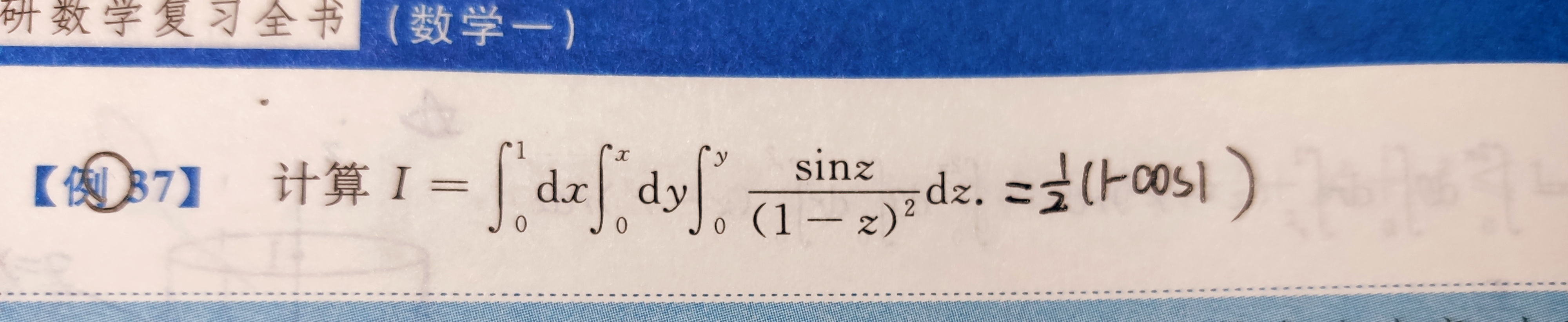
二重积分极坐标下的交换积分次序

---

变上限累次积分求导

---

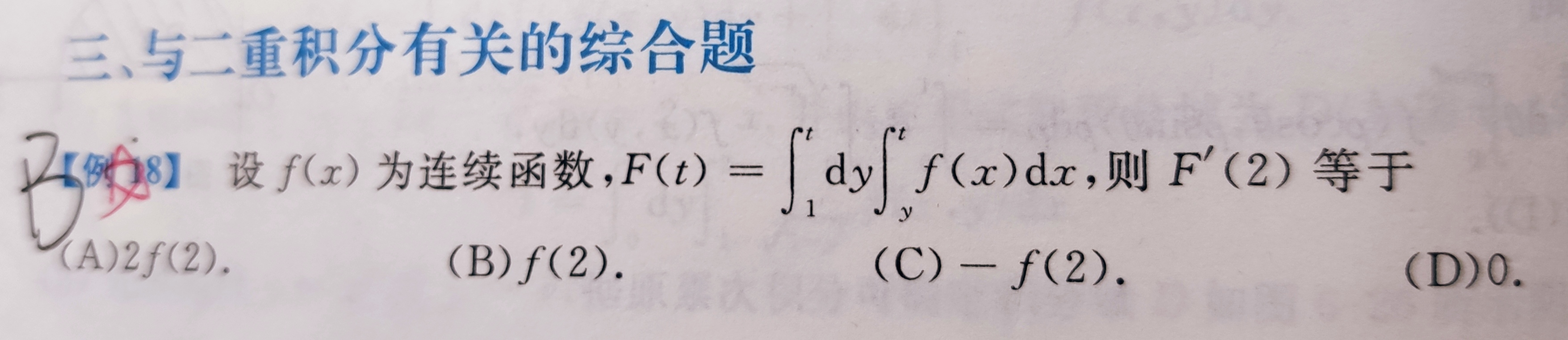
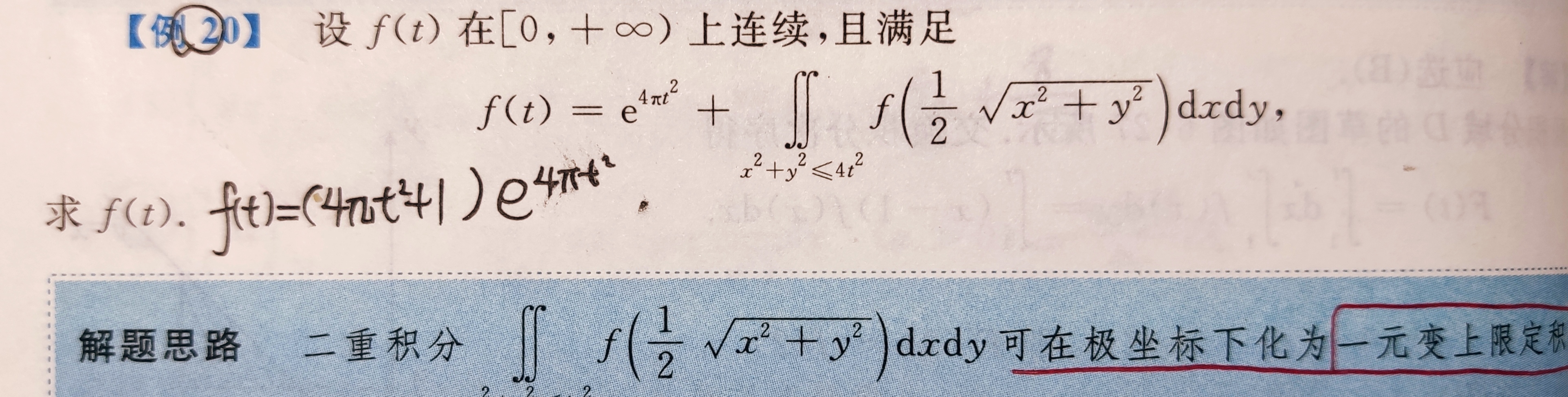
方程形式

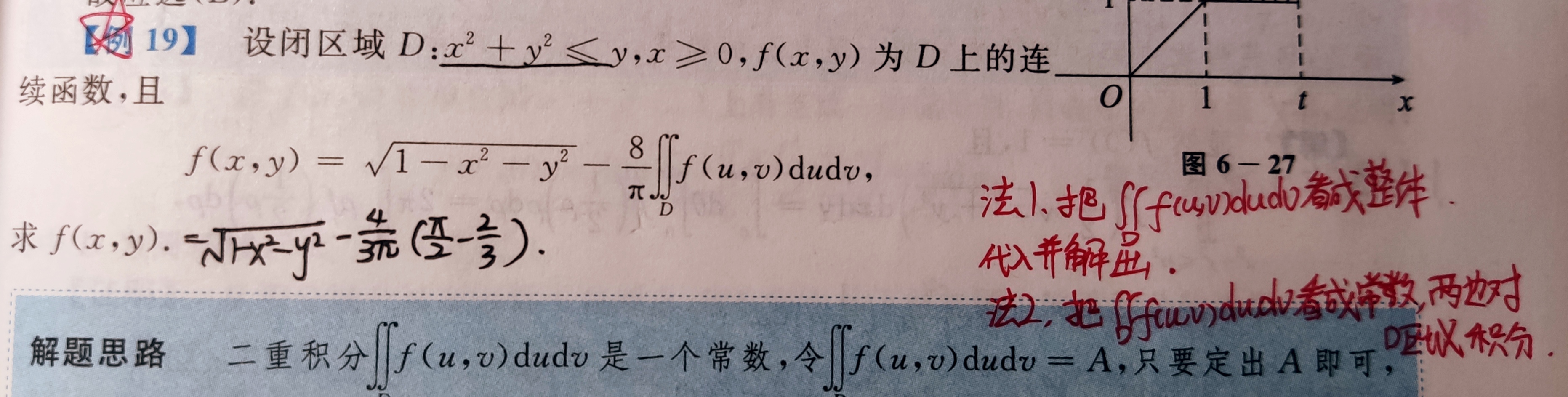
分段函数结合二重积分

参数方程结合二重积分

---

不等式的证明

---

课本补题

---

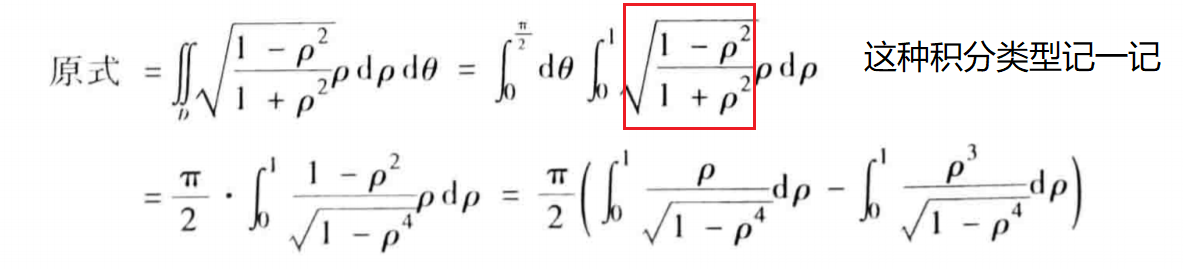
补充几个实记图

---