今天反思一下卡诺图化简法中的注意事项。另，文章太短被限流了，因此补充一下竞争冒险相关的知识点。
一、卡诺图化简法
卡诺图方法在这里不介绍了，这种方法看起来简单，但如果不熟悉的话很容易出错，因此要对花圈的规则比较熟悉。
①圈越少越好
②圈越大越好
③不能有多余圈，也不能有遗漏
④化简结果可能不同。
这里说一下我个人理解不到位的地方，如果，①和②相矛盾了该怎么办？
比如说这个图，我可以像图中这样，圈四个2格的圈，但我也可以在中间圈一个4格的圈+4个1格的圈，哪种化简出来最简呢。
实际上，应以①圈越少越好为优先，因为逻辑表达式化简的本来目的就是减少项数，如果为了追求单个圈的大小而增加了圈的个数（增加项数），那么这是南辕北辙的行为，因此，上图所示的圈法才是正确的。
文中未标明的参考文献在此处列出：
(60条消息) 卡诺图化简法_Samplay的博客-CSDN博客_卡诺图化简法
二、竞争冒险
1.竞争与冒险的定义：
（1）竞争的定义：比较正规的定义是“门电路的多个输入端同时发生方向相反的跳变的现象（比如一个0变1另一个1变0）”。
在网络中也经常出现另一种定义：“门电路的多个输入端的信号，由于路径时延的不同，导致到达门电路输入端的时间不同的现象”。
这两种定义是没有冲突的，如果要发生冒险那么需要上述两个定义的现象同时发生。
（2）冒险的定义：由于竞争的发生而导致门电路输出存在毛刺的现象，叫做冒险。
要注意，有竞争不一定有冒险，有冒险一定有竞争。
2.竞争冒险的判别
（1）代数法。
详见：(60条消息) 竞争冒险_宇哥啊的博客-CSDN博客_竞争冒险
注意区分0型冒险和1型冒险。
（2）卡诺图法
通过寻找卡诺圈的相切部分来判断是否有竞争的现象
这里要尤其注意判断竞争冒险的第二个条件，即“没有被另外的卡诺圈包围”，如果相切处被其他卡诺圈包围，那么是不会出现竞争冒险的。举个例子吧：
如上图所示，两个卡诺圈相切（ABCD=0101和ABCD=1101处相切），且相切处的两个最小项没有被另外的卡诺圈包围，此时，有竞争冒险
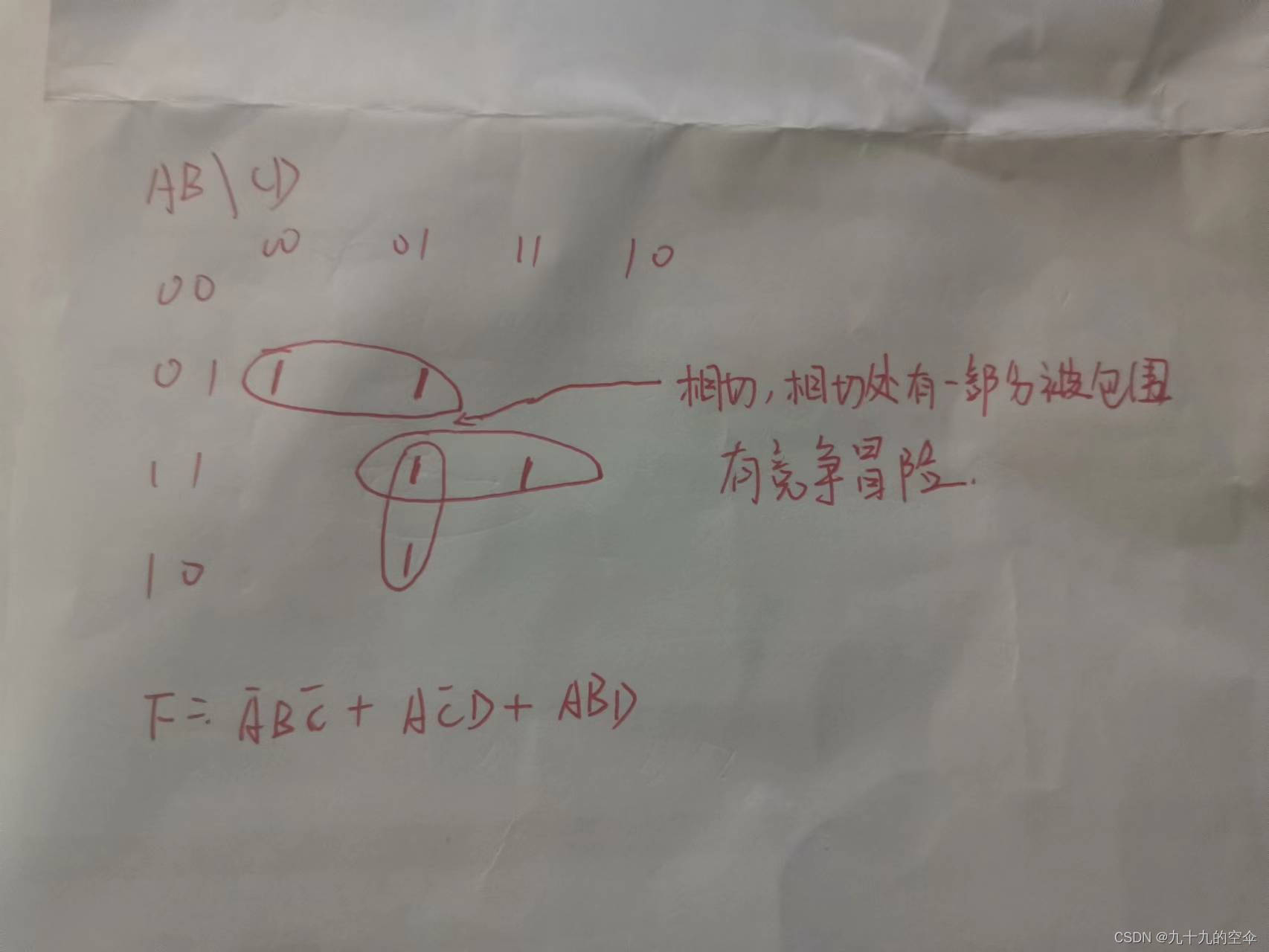
如上图所示，同样的相切位置，只不过这一次其中一个最小项被第三个卡诺圈包围，此时，仍没有竞争冒险。
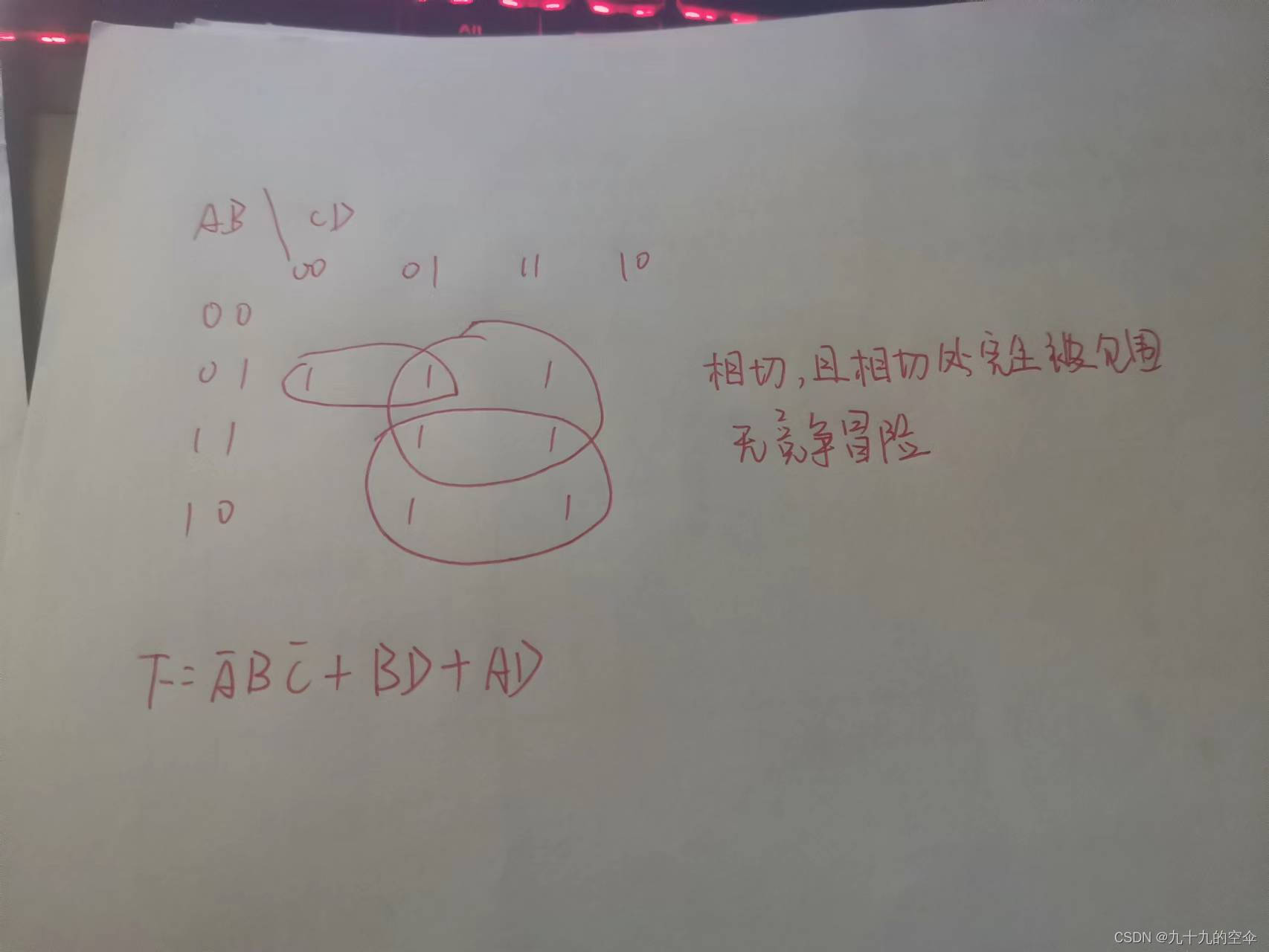
最后一个例子，还是同样的相切位置，但是相切处的两个最小项都被另外的卡诺圈包围，此时，无竞争冒险。
所以我们可以得出结论，判断出现竞争冒险的条件是“两个卡诺圈相切，且相切部分所涉及的两个最小项没有被其他卡诺圈完全包围，此时，有竞争冒险”。
如果相切，但是相切处的两个最小项都被其他卡诺圈包围，那么，没有竞争冒险。
PS：感觉还是代数法简单一点。
3.竞争冒险的处理方法
（1）加电容
缺点是输出波形质量变差。
（2）加选通脉冲。
等待0型脉冲或者1型脉冲产生以后，再对输出进行采样，避开了可能的脉冲信号。
（3）加冗余项
加冗余项不会改变电路逻辑功能，以上图为例，冗余项是B(~C)D，当BCD！=101时，F的表达式和加冗余项之前相同，因此此时功能是相同的，而当BCD=101时，D=A+(~A)+1，加不加冗余项都是1，因此也不会改变电路逻辑功能。
在这里，三种情况下都可能 发生竞争冒险，那么就要加三个冗余项，分别是
(~B)C、A(~C)、(~A)B
加了这么多冗余项，直觉上感觉电路的输出会被更改，但实际上电路的逻辑功能仍然是不会被更改的。因为：
F0=A(~B)+(~A)C+B(~C) 这是加冗余项之前的.
F1=F0+(~B)C 加了一个冗余项
F2=F1+A(~C) 加了二个冗余项
F3=F2+(~A)B 加了三个冗余项
之前已经证明F0和F1逻辑功能相同，同理我们可以证明F2和F1相同，F3和F2相同，因此F0和F3的逻辑功能不变，他们具有相同的真值表。
另外，冒险可以分为0型冒险和1型冒险，也可以分为逻辑冒险和功能冒险，详见：
(60条消息) 竞争冒险_宇哥啊的博客-CSDN博客_竞争冒险
以上就是我对竞争冒险的个人看法，如有错误请指出，大家一起讨论提高。
文中未标明的参考文献在此处列出：
(60条消息) 数字电子技术基础（九）：竞争—冒险现象成因及消除_QNee的博客-CSDN博客_竞争冒险产生的原因以及如何消除
5915
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
