det是什么意思矩阵_什么是dx——无穷小量的原理

高等数学是多数大学生进入大学的第一门课程，但有趣的是：很多大学生在学完高等数学后，并没有理解到什么是dx。往往对dx的印象停留在「一个无穷小的量」、「要多小有多小」、「比任意ε都小」等这样的初步直观印象。当然，这些说法的确都是正确的，但这无法解决无穷小量间的关系问题。

例如：如果问为什么dy=f'(x)dx？如果把dx和dy理解为两个独立而不相关的无穷小量，这一现象都变得无法理解。而如果无法理解到dx与dy的关系，对于后期多元函数的各种诡异而变化莫测的换元方法就更加难以理解了。光凭借死记硬背，或许应付高数的考试是足够的，但是在笔者看来，这不能算作学会了高数。从这个意义上，或许物理学系的对无穷小量dx理解得最透彻，因为他们做题时要一直对dx进行各种换元与分析。

在本文中，笔者会以讨论的形式，不断提出问题，以与读者讨论的方式来研究分析这些问题，最终探讨出一个答案。关于这些结论中的部分，笔者是有严谨的证明。但是本文的目的是培养对无穷小量dx的直观认识，故笔者将略去这些证明。对于少数笔者认为有必要让读者了解的关键步骤，笔者会单独提出来讲思路，但尽可能地不涉及具体的证明细节。

总之，本文的目的是培养读者对无穷小量的直觉。希望读者在阅读本文时，不要将本文当作教科书生硬地“学习”，而是要想象笔者站在你的面前，在与读者“探讨”问题。全文第一部分我将采用对话体，笔者自称「我」，对话对象称为「小羽咲」（这是设定，不要吐槽啦）。请读者自行代入「小羽咲视角」。

当然，由于本文是面向各个知识段的读者的，在全文开始之前，我将在下面罗列一些有必要掌握的定理，当读者遇到没有学过的内容时，可以参考以下说明进行补充阅读。

---

以下是公式定理说明表（已经了解这些定理的读者，可以直接跳到下一环节）

---

本文最理想的读者是学习完高等数学的《多元函数的重积分》及其之前的所有内容的读者，对于没有修习这些内容的读者，下面将列举你们所必要了解的一些内容/定理^[1]：

（已经了解这些定理的读者，可以直接跳到下一环节）

一、对于没有修习《高等数学（下）》的读者，你们需要了解的有：

1、全微分公式

即：

（笔者注1：事实上，本质上，隐函数求导公式可由该公式导出。在本文中，由于该公式具有非常好的对称美性质，我们将十分频繁地应用该公式）

（笔者注2：该公式具有很好的对称美性质，我们可以将该公式推广到n维情形，对于n维情形的该公式，我们也称之为「全微分公式」）

2、全微分形式不变性

即：在全微分公式

的基础上——

如果u，v是中间变量，即有

，

的换元关系，则有：

（笔者注1：通俗地说，就是：不管把什么当成自变量，dz都可以表示为这一组自变量(下以x为例)对应的

的求和）

（笔者注2：换言之：「全微分形式不变性」保证了——dz可以被写成对应的全微分，这一点与你选择的变量是自变量或中间变量无关）

（笔者注3：高阶微分不再具有微分形式不变性，这一点与「一元高阶微分不具有形式不变性」类似）

3、隐函数求导法则（偏导）

即：

（其中

代表F对x的偏导）

这一推导可以类比二元隐函数方程求导记忆——

我们通过对

左右全微分可以知道：

即：

同理，多元（未知数大于等于2）函数，不过是把d换成了∂罢了。

即：

二、对于没有修习《高等数学（上）》的读者，你们需要了解的有：

1、复合函数的链式求导法则

即：

（笔者注：这也暗示了微分的一大特性：微分可以被当成实体参与运算）

2、各种求导法则

例如乘积求导法则、除法求导法则等

3、求偏导

所谓求偏导，即把其他变量当成常数，只对指定变量求导，符号用

表示。如

表示z对x求偏导。

举例^[2]A：

，即把y当成常数，y x相当于斜率为y的一次函数。

B：

，不管你什么花里胡哨的，后面的统统当成常数处理，只对x求导。

C、

，即把y看成常数，我们知道

求导是

，同理把k换成y即可

4、隐函数求导法则

我们知道任意函数

总能被看作方程

更广义地，当y=f(x)不容易被显式地写出时，就可以将其写成一个方程

的形式，我们称之为隐函数方程。

（例如想要绕开反三角函数，就可以把

写成

，这就确定了一个方程

）

这样确定了一个隐函数，如果把

人为添加一个维度z，即看作

且z=0，那么对左右全微分，左面z=0微分显然为0，右面微分按照「全微分公式」（见

「公式定理说明表」一、1）即为

，导数自然是

。

（笔者注：看起来这里写的隐函数求导法则与《高等数学（上）》不同，但实质上是相同的。至于为什么，这就留待读者自行思考了）

---

以下是正文部分

全文采取对话体，请脑补「笔者」为「我」，脑补「读者」为「小羽咲」或「羽咲」

---

第一部分：从全微分不变性说起

---

我：小羽咲，你知道

等于多少吗？

（注：

是偏微分算符，意思是分子对分母求偏导，所谓求偏导即把其他变量看成常量，对分母求导，具体说明见

「公式定理说明表」二、3）

羽咲：这个还不简单吗？把y当成常数，这个就是最简单的求导，显然为1啊！

我：（露出阴险的笑容）

羽咲：（有一种阴谋的气息）

我：谁说的y相对x是常数了呢，你被我坑啦！

羽咲：？？？（黑人问号）

我：其实我认为

，其中u与x无关，这样

。哈哈哈，略略略……（发出欠打的笑声）

羽咲：怎么可以这样，x、y不是垂直的吗？垂直的话两者肯定无关啊！

我：想不到吧，哈哈哈哈哈（欠打ing）

配图配错了，懒得改了，意思就是x轴与y轴不一定垂直，在这里面我画成了x+y=z嘤嘤嘤

羽咲：お兄ちゃん、バカ！！！！（并将我拉入黑名单）

我：等等！羽咲别走！我再也不抬杠了！本当に申し訳ありません、お優し羽咲様（小仓朝日附体）

………………（一天后）

羽咲：哼（一脸不爽）！这个问题你得好好给我讲清楚，不然就……（比手刀姿势）

我：嗯嗯，我保证再也不抬杠了（本当に申し訳ありません、お優し羽咲様×2）

我：回到正题，我们都知道全微分公式

，那么自然地，如果

，就有

。

这样我们就能自然得出此时：

了。

（注：全微分公式见「公式定理说明表」一、1）

羽咲：你昨天不还说

吗？怎么现在又变成1了？

我：对，这就是问题的根源——事实上，

是

指代对象不明的。回忆求偏导的意义：把其他变量当成常数，对分母求导。那么问题来了——什么叫「其他变量」呢？

羽咲：这不显然x是变量，y是其他变量吗？你上面求全微分不也这么写的吗？

我：对，在上面我举的例子里，的确是指代对象明确的——因为我写了

和

，自然是默认x与y是两个无关的变量。但是如果没有指明的话，类比上面我举的例子，我可以令y=x+u，其中u是与x无关的变量。那么同理，为什么一定是x与y无关呢？

羽咲：那应该怎么办才好呢？

我：回忆《线性代数》里面的知识，我们可以把向量组

、

、

当做空间的一组「基」，那么我们也可以把向量组

、

、

当做空间的一组「基」。这样的选择有无限多种，还记得需要且仅需要满足一个什么条件吗？

羽咲：是线性无关对吧。或者说一组基中任意一个向量都不能由另一个向量线性表出。我记得这好像是一个被叫做「秩(rank)」的东西，只要变换矩阵的「行列式(det)」不为0，那么就线性无关。反之则线性相关。

我：对的，事实上，这个变换矩阵被称为「雅可比矩阵(Jacobian)」，不过考虑到篇幅，我对此按下不表。

羽咲：那既然你之前和我抬杠，那我现在也要杠一波。假如我设定基底为

和

，那么

全微分等于多少呢？

我：

把x看成变量，则

把y/x看成变量，则

即

羽咲：那么我们再把dx和dy看成一组新基底，又可以得到

，代入回去就是

。这也恰好印证了

全微分不变性。

我：是的。所谓全微分不变性，不过是从不同的基底分解dz，无论是哪一种分解，本质上都是相同的。

羽咲：但如果我把

看成分解的基，即

，那这不就只用了

一个基向量就完成分解了吗？

或者我把它看作

这些基的组合，其中u，v等等都与x、y都无关，那么我就可以分解为

。

我：你咋比我还能杠啊（看到羽咲紧攥着的拳头）……哦不不，没什么。这个问题说起来比较复杂，你看前面du、dv前面系数不都是0嘛，简而言之就是有多少个变量就最多有多少个非0的基向量，当然，比它少自然也是可以的，不过往往来说，我们习惯分解为dx、dy、dz这种简单的向量，这也是我们看到

第一反应是1的原因，这也不能说是错的，只不过这种表述的确不规范。平时习惯上，我们还是认为它是1的。

---

第二部分：无穷小元素的关系

---

经过前面的小剧场，相信大家对「全微分」有了一些基本的认识。值得注意的是，以上这些操作本质上是不严谨的，事实上，保证这些操作合法性的正是全微分形式不变性这一点。切记不能用它作为全微分形式的证明，否则将陷入循环论证的误区。当然，本篇的基调是直觉，以直觉为主线，我们只需要知道保证上述操作合法性的是全微分形式不变性就可以了。

正是因为全微分的形式不变性，我们可以把「微分」看作一个「实体」。什么叫「实体」呢？在我的定义里，「实体就是可以进行『加、减、乘、除』」。当然，1/dx是不被允许的，减的时候也要注意dx-dx可能会残余「高阶无穷小」，乘的时候dx dy往往表示面积^[3]，除的时候要注意

， 因为高阶微分不具有形式不变性，之所以一阶微分可以保证除法，是因为「一阶微分具有形式不变性」。虽然在前面说到本篇的基调是直觉，但是也不能随便乱用。这里只是列举了一些常见的误区，其他误区需要读者逐渐积累发现。

在下面部分的内容中，我们的吉祥物羽咲酱就此退场了。由于下面的环节是比较枯燥的，所以我会尽可能地压缩篇幅。

---

往往来说，微分都具有具体的物理含义。我们可以认为「微分」是「一个实际物体的代表元素」，例如

，其中dm就是物体质量的代表元素，如果我们想要求整个物体的质量，那么就是只需要将其积分即可。

。

同理，恰好今天物理课在讲电磁学，拿电磁学举个例子。

例题：假设与一个长为l，带电量为+q的均匀带电细棒的中垂线距离为R处有一个点M，求该点的场强大小。（见下图）

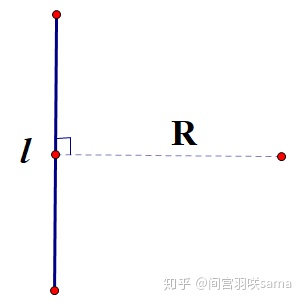
首先，由对称性，显然沿杆方向分量为0，只考虑中垂线方向。

用微元法分析，首先在细棒l上取出一个

长度的代表元素，其带电量

为

，假设距离中垂线为x，那么电场强度的分量

。

积分即为：

我们注意到：我们把dx、dq、dEx都是有物理含义的实体，它们都相当于一个实际物体的代表元素。

---

那么，我们就对这些代表元素的关系进行分析

下面，由于对话体写起来太费时间，我将以断言式的方式先给出各种微小元素的定义。读者将发现：这些定义中很多是显然的，但我们可以由这些显然的定义推导出整本高数的所有微元换元公式。

当然，这里的推导会频繁的应用到「隐函数求导公式（偏导）」，希望读者要将这一公式当成一个显然的、可以秒答的公式。

（注：隐函数求导公式（偏导）见「公式定理说明表」一、3）

1、弧长元素

结论：在一元函数里，长度元素为

2、面/体积元素

结论：在二元函数里，面积元素为

结论：在三元函数里，体积元素为

3、投影面积元素

其中投影平面垂直与什么，∂u就等于什么。
并且规定∂F可以与dx、dy、dz中任意一者结合，以dx为例，即为∂F/∂x

4、单位曲面法向量

注：分母那一坨只是为了单位化

5、单位曲面元素

规定∂F可以与dx、dy、dz中任意一者结合，以dx为例，即为∂F/∂x

---

下面是对上面公式的具体说明

上面的公式是高度抽象的，如果不加以说明，大家根本不知道如何应用它们。下面，我将阐述这些公式的含义，以及其应用方式。

在此之前，先定义几个符号：

1、

定义：将偏导数

简记为

或

2、

定义：将雅可比行列式

简记为

3、雅可比行列式可取倒数^[4]：

定理：

---

1、弧长元素

结论：在一元函数里，长度元素为

这一结论当然是显然的，我们要研究的是如何将

变化为

、

、

这些其他微小元素。

变换方法：

A、 变换为dt

原理： 方法为同时乘以dt与除以dt，分母上的dt与根号里的dx、dy结合，就变成了dx/dt、dy/dt了。

B、变换为dx

原理： 思路上与变换为dt一样，就是把t换为了x。

C、变换为dθ

原理： 此处利用了等式

，dy对应的等式同理。然后与前面类似的思路，同时乘以除以dθ即可。

2、面/体积元素

结论：在二元函数里，面积元素为

结论：在三元函数里，体积元素为

这一结论阐述的是多元函数的换元方法，正如一元函数有

一样，如果我们把

看作与雅可比行列式一样的伸缩因子。多元雅可比行列式也有类似的性质，即：

。

来具体举几个例子——

A、

B、

3、投影面积元素

其中投影平面垂直与什么，∂u就等于什么。
并且规定∂F与dx、dy、dz中任意一者结合，以dx为例，即为∂F/∂x

例如投影平面为xOy，则∂u=∂z。

如欲以dxdy来表示之，则令∂F与dz结合，即：

。

如欲求得dydz来表示之，则令∂F与dx结合，即：

再考虑到隐函数求导公式：

则：

4、单位曲面法向量

这一点是直观的。

首先说明：分母乘的那一坨是分子向量的模长，相当于单位化。

至于这为什么是法向量，一个直观的理解就是：考虑到全微分，有：

，故有：

。而后者的几何意义为曲面的任一微小向量，而前者与任意微小向量都垂直，自然是法向量了。

5、单位曲面元素

这里结合3的投影面积元素就显得好理解了。

投影面积元素

，其中u是被投影平面法向量。

单位曲面元素可以看做三个投影面积元素的平方和，也就是本公式。

当然，这个式子只是隐式地指出了单位面积元素，想要得到我们平时常用的公式，就需要把∂F与d结合。例如用dx dy表示（即消去dz），就可以把∂F与dz结合，即为：

放到根号里去则是：

利用隐函数求导公式化简即为：

---

第三部分：无穷小元素的在空间解析几何的代表性质

---

先从一个问题看起——

原来有同学问我：为什么形如

表示一个平面呢？

我给他的回答是：

考虑上面任意一点

这个方程又可以写成：

又可以看成向量

与

的点乘，即：

这表明：该方程上任意一点与点M构成的向量b都与向量a垂直。

这样的点的集合就是一个平面。

---

上面如果以「把dx看成实体」的角度看这个问题，这就变得更清晰了。

考虑方程：

进行全微分：

写成向量点乘：

这表明：该方程任意一点上的微小变化向量都与常向量

垂直。

这样我们不仅可以得到「这是一个平面」的信息，还可以知道任意一点的法向量。

这也引出了我们「求任意光滑空间曲面的法向量」的方法——

---

1、「求任意光滑空间曲面的法向量」的方法

首先，我们知道：通常来说^[5] ：

表示一个空间曲面。

表示一个空间曲线。

那么下面我将阐述——如何利用dx的实体性求解空间曲面的法向量/空间曲线的切向量。

先举一个简单的例子：

A、求球面

上任意一点的法向量。

解：将其全微分：

可以得到：

我们知道，与任意微小增量都垂直的必然是法向量。

故

为其法向量。

当然，从特殊到一般，我们可以推广得到下面命题——

B、

上任意一点法向量为

证明：将其全微分：

可以得到：

我们知道，与任意微小增量都垂直的必然是法向量。

故

为其法向量。

C、应用B解A

球面方程可以写成：

剩下同2操作即可。

---

2、求解任意空间曲线的切向量

通过几何直观，我们容易发现

是该点的切向量。

考虑方程：

全微分可得：

如果我们只把dx、dy看成变量，其他看成常数，这就是一个二元一次方程组。

以求解dx为例子，这里可以通过《线性代数》的「克莱姆法则(Cramer's Rule)」直接写出答案：

。

化简即为：

同理可以求得dy与dz的关系，可以发现：

即

与

同向。

那么自然方向向量就是：

了

---

其余空间几何的分析方法，本质上都是与上面两者等价的。读者应该理解到

作为任意微小增量向量的含义，通过其几何含义，得到各种空间几何的式子。

例如——

通过变形得到：

。

其它的读者可以自行摸索，通过几何对称的公式推导自己具体题目需要的公式是一件有趣的事情。

参考

1. ^这里略去了一些常见的条件，例如假设函数可微/可导/连续等，这是为了让读者直观理解定理
2. ^此处举例写法事实上是不严谨的，具体原因会在正文提到
3. ^（以下内容是根据大佬舍友提示）当然，dx与dy有时候不是简单的数量（标量）相乘关系，在有方向问题的情况时，dx与dy应当理解两个向量，它们两个的乘积相当于叉积（而不是标量乘积），得到的是一个叫做「二重向量」的东西。例如在这个框架下，dx dy=-dy dx。当然，为了处理方便，我在下面引入了一些技术，将其“封装”为了标量处理。至于这一技术的合理性的论证，考虑到篇幅，不予论证。
4. ^事实上，这显然是需要证明的，否则我们完全有理由相信这一定理不成立。读者可将其作为习题尝试证明之。
5. ^如果不是刻意构造一些诡异的东西，比如x^2+y^2+z^2+1=0这种实数域无解的东西的话，下面的断言总是成立的