简介:细化算法是图像处理中的关键技术,主要用于提取二值黑白图像的骨架,实现物体形状的紧凑表示。该技术广泛应用于模式识别、图像分析和生物医学图像处理等领域。本文项目基于VC++平台,采用C++语言实现细化算法,包含Hilditch算法、Medial Axis Transform(MAT)、迭代腐蚀与膨胀等多种主流细化方法。项目资源中包含详细代码和说明文档,帮助开发者掌握细化算法的核心实现过程,并提升图像处理实战能力。
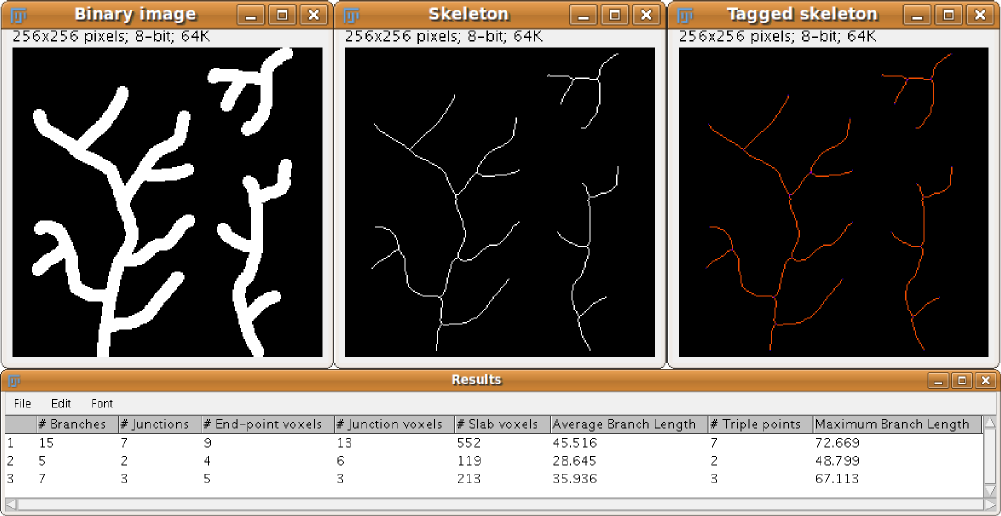
1. 图像细化算法概述
图像细化是数字图像处理中的核心操作之一,主要用于提取图像中物体的骨架结构。通过将图像中的目标对象压缩为一条单像素宽的中心线,细化算法在保留原始形状特征的同时显著降低数据维度,为后续的模式识别、形状分析与特征提取提供了高效基础。
本章将从图像细化的基本原理入手,探讨其在二值图像处理中的关键作用,特别是骨架提取过程中对拓扑结构和几何特征的保持要求。同时,我们将简要介绍几种主流细化算法,如Hilditch算法、Medial Axis Transform(MAT)算法以及基于数学形态学的迭代腐蚀与膨胀方法,为后续章节的深入分析与实现奠定理论基础。
2. 二值图像处理基础
二值图像处理是图像细化和骨架提取的基础环节,其核心在于将原始图像转化为只有黑白两种像素值的图像形式。通过二值化操作,不仅可以有效降低图像的复杂度,还能为后续的拓扑结构分析、形态学操作和骨架提取提供清晰的边界与结构信息。本章将从二值图像的基本概念入手,逐步深入探讨其预处理方法、拓扑结构特性以及数学形态学的基本运算,为理解图像细化算法的底层逻辑打下坚实基础。
2.1 二值图像的基本概念
2.1.1 二值图像的定义与表示
二值图像(Binary Image)是指每个像素仅取两个可能的灰度值:通常为0(黑色)和255(白色),分别表示背景和前景。其数学表示为一个二维矩阵 $ B(x, y) $,其中:
B(x, y) =
\begin{cases}
0, & \text{背景} \
1, & \text{前景}
\end{cases}
在实际图像处理中,常使用 numpy 数组来表示二值图像。例如,一个 $ 3 \times 3 $ 的二值图像矩阵可以表示如下:
import numpy as np
binary_image = np.array([
[0, 1, 0],
[1, 1, 1],
[0, 1, 0]
])
逐行分析:
- 第1行导入
numpy库,用于数组操作。 - 第4~7行定义了一个3x3的二维数组,模拟一个简单的二值图像。
参数说明:
-
0表示背景; -
1表示前景(物体); - 数组中的每个元素对应图像中的一个像素点。
2.1.2 二值图像在计算机视觉中的应用
二值图像广泛应用于图像分割、目标检测、文字识别和骨架提取等领域。其优势在于:
- 计算效率高 :仅需处理两个灰度级;
- 便于结构分析 :如连通区域分析、边界追踪;
- 适用于形态学操作 :如腐蚀、膨胀等。
例如,在OCR(光学字符识别)中,将图像二值化后可以更清晰地提取字符轮廓,便于后续识别。
| 应用领域 | 二值化的作用 |
|---|---|
| OCR识别 | 提取字符轮廓 |
| 医学影像 | 分割器官轮廓 |
| 工业检测 | 检测缺陷区域 |
| 骨架提取 | 为细化算法提供输入 |
2.2 图像预处理技术
2.2.1 图像二值化方法
图像二值化是将灰度图像转换为二值图像的过程,常用方法包括:
- 全局阈值法 :对整幅图像使用一个统一的阈值;
- 局部阈值法 :根据图像局部区域动态调整阈值;
- Otsu算法 :自动计算最优阈值。
以OpenCV为例,使用Otsu算法进行二值化:
import cv2
import numpy as np
# 读取灰度图像
gray_image = cv2.imread('image.jpg', 0)
# Otsu二值化
_, binary_image = cv2.threshold(gray_image, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)
逻辑分析:
- 第4行使用
cv2.imread读取图像并转为灰度图; - 第7行使用
cv2.threshold执行二值化操作,参数cv2.THRESH_OTSU表示自动选择最佳阈值; - 返回值
binary_image即为二值图像。
参数说明:
-
0和255是二值化的两个灰度值; -
cv2.THRESH_BINARY表示将大于阈值的设为255,小于的设为0; -
cv2.THRESH_OTSU表示使用Otsu算法自动计算阈值。
2.2.2 噪声去除与图像增强
二值图像在获取过程中可能受到噪声干扰,需进行去噪处理。常用方法包括:
- 形态学操作 :开运算(去除小对象)、闭运算(填充空洞);
- 中值滤波 :有效去除椒盐噪声;
- 边缘增强 :提高图像的清晰度。
# 使用中值滤波去除噪声
denoised_image = cv2.medianBlur(gray_image, 3)
# 形态学开运算
kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (3, 3))
opened_image = cv2.morphologyEx(binary_image, cv2.MORPH_OPEN, kernel)
逻辑分析:
- 第2行使用中值滤波对灰度图进行去噪;
- 第6~7行执行形态学开运算,去除小面积噪声;
-
cv2.getStructuringElement用于定义结构元素。
参数说明:
-
3表示滤波窗口大小; -
MORPH_RECT表示矩形结构元素; -
(3,3)表示结构元素的尺寸。
2.3 图像的拓扑结构分析
2.3.1 连通性与边界定义
在二值图像中,连通性是分析物体结构的基础。通常定义两种连通方式:
- 4连通 :仅上下左右相邻;
- 8连通 :包括对角相邻。
graph TD
A[像素点] --> B[4连通]
A --> C[8连通]
B --> D[(0,1)]
B --> E[(1,0)]
B --> F[(0,-1)]
B --> G[(-1,0)]
C --> H[(1,1)]
C --> I[(1,-1)]
C --> J[(-1,1)]
C --> K[(-1,-1)]
说明:
- 该图表示一个像素点的4连通与8连通邻域;
- 4连通只考虑直接相邻,8连通还包括对角线方向。
2.3.2 骨架线的拓扑保持要求
骨架提取要求在细化过程中保持图像的拓扑结构不变,即:
- 不断开连接;
- 不产生新的连接;
- 不改变端点数量。
为满足这些要求,细化算法必须遵循严格的判定条件,例如Hilditch算法中的8个判断规则。
2.4 二值图像的数学形态学基础
2.4.1 腐蚀与膨胀操作
腐蚀(Erosion) 和 膨胀(Dilation) 是形态学的基本操作,常用于图像细化和结构分析。
# 腐蚀操作
eroded_image = cv2.erode(binary_image, kernel, iterations=1)
# 膨胀操作
dilated_image = cv2.dilate(binary_image, kernel, iterations=1)
逻辑分析:
- 第2行执行腐蚀操作,使前景区域缩小;
- 第5行执行膨胀操作,使前景区域扩大;
-
iterations=1表示进行一次迭代。
参数说明:
-
kernel是结构元素; -
iterations控制操作次数。
2.4.2 开运算与闭运算的应用
开运算(Opening) 先腐蚀后膨胀,用于去除小对象;
闭运算(Closing) 先膨胀后腐蚀,用于填充小孔洞。
# 开运算
opened_image = cv2.morphologyEx(binary_image, cv2.MORPH_OPEN, kernel)
# 闭运算
closed_image = cv2.morphologyEx(binary_image, cv2.MORPH_CLOSE, kernel)
逻辑分析:
- 第2行执行开运算,去除图像中的孤立点;
- 第5行执行闭运算,填充图像中的空洞;
- 这两个操作对图像的结构有重要影响,常用于预处理。
| 操作类型 | 作用 | 示例 |
|---|---|---|
| 开运算 | 去除噪声 | 消除孤立像素 |
| 闭运算 | 填充空洞 | 闭合断点 |
总结:
通过对二值图像的定义、表示方法、预处理技术、拓扑结构分析以及形态学操作的深入探讨,我们可以清晰地理解其在图像细化中的基础作用。这些知识为后续章节中具体细化算法的设计与实现提供了理论依据与技术支撑。
3. 骨架提取原理详解
骨架提取是图像细化的核心任务之一,其目标是将原始图像中的目标区域简化为一条单像素宽度的线条结构,同时保持其拓扑不变性与几何特征。骨架不仅能够保留原始形状的关键信息,还为后续的模式识别、特征提取和形状匹配提供了强有力的支持。本章将从骨架的基本定义出发,深入剖析骨架提取的数学原理与算法思路,结合具体示例说明细化操作的实现逻辑与评估标准。
3.1 骨架的基本定义与性质
骨架(Skeleton)是描述图像目标区域中心结构的一种抽象表达形式。它不仅保留了原始形状的连接性与几何特征,而且具有最小的表示冗余度,因此在图像识别、模式匹配等领域中被广泛应用。
3.1.1 骨架的数学描述
在数学形态学中,骨架通常被定义为一组“最大内切圆”的中心点集合。对于任意一个目标区域 $ R $,其骨架 $ S $ 可以表示为:
S = \left{ p \in R \mid \exists r > 0, B(p, r) \subseteq R \land \forall r’ > r, B(p, r’) \not\subseteq R \right}
其中:
- $ p $ 是图像中的一个像素点;
- $ B(p, r) $ 表示以点 $ p $ 为圆心、半径为 $ r $ 的圆;
- $ R $ 表示目标区域;
- $ S $ 是骨架点集合。
该定义表明,骨架点是图像中所有能够容纳最大内切圆的点。这些点位于形状的“中轴”上,构成了骨架线。
3.1.2 骨架线的几何特性
骨架线具有以下关键几何特性:
| 特性 | 描述 |
|---|---|
| 单像素宽度 | 骨架线应保持单像素宽度,避免出现分支或断裂 |
| 拓扑保持 | 骨架应保持原始形状的连通性、孔洞结构和分支关系 |
| 中心性 | 骨架点应尽可能位于原始形状的几何中心 |
| 稳定性 | 对于图像的轻微扰动(如噪声),骨架应具有一定的鲁棒性 |
这些特性构成了骨架提取算法设计与评估的基础。在实际应用中,骨架的质量往往取决于是否能够良好地保持这些几何属性。
3.2 骨架提取的核心算法思路
目前主流的骨架提取方法主要分为两大类: 基于距离变换的方法 和 基于边缘追踪的方法 。它们分别从不同的角度实现骨架的提取,适用于不同的应用场景。
3.2.1 基于距离变换的方法
基于距离变换(Distance Transform)的方法是一种广泛使用的骨架提取策略。其核心思想是:
- 对二值图像中的前景区域(即目标区域)进行距离变换,计算每个前景像素到最近背景像素的距离。
- 找出距离变换图像中的局部极大值点,这些点即为骨架点。
算法流程图如下:
graph TD
A[输入二值图像] --> B[距离变换计算]
B --> C[局部极大值点检测]
C --> D[骨架提取结果]
示例代码(Python + OpenCV) :
import cv2
import numpy as np
# 读取二值图像
img = cv2.imread('binary_image.png', 0)
dist = cv2.distanceTransform(img, cv2.DIST_L2, 5)
local_max = np.zeros_like(dist, dtype=np.uint8)
local_max[dist == dist.max()] = 255 # 假设最大值为骨架点
skeleton = cv2.ximgproc.thinning(local_max) # 细化处理
cv2.imshow('Skeleton', skeleton)
cv2.waitKey(0)
代码解释:
- cv2.distanceTransform :计算每个前景点到最近背景点的欧氏距离;
- DIST_L2 表示使用欧氏距离;
- local_max 提取距离图中的局部极大值点;
- cv2.ximgproc.thinning 对局部极大值图像进行细化,提取单像素骨架线。
该方法适用于规则形状的骨架提取,但在处理复杂形状时可能出现断裂或分支过多的问题。
3.2.2 基于边缘追踪的骨架生成
边缘追踪方法通过检测目标区域的边缘轮廓,沿着边缘向内收缩,逐步提取骨架线。其基本流程如下:
graph TD
A[输入图像] --> B[边缘检测]
B --> C[轮廓提取]
C --> D[轮廓收缩与骨架生成]
D --> E[骨架输出]
这种方法适用于轮廓清晰的目标,尤其在医学图像和工业检测中表现良好。
示例代码(OpenCV轮廓骨架化) :
import cv2
import numpy as np
img = cv2.imread('binary_image.png', 0)
contours, _ = cv2.findContours(img, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
# 创建空图像用于绘制骨架
skeleton = np.zeros_like(img)
# 轮廓逐步收缩
for cnt in contours:
for i in range(10): # 模拟收缩10次
epsilon = i * 0.01 * cv2.arcLength(cnt, True)
approx = cv2.approxPolyDP(cnt, epsilon, True)
cv2.drawContours(skeleton, [approx], -1, (255), thickness=cv2.FILLED)
cv2.imshow('Skeleton via Edge Shrinking', skeleton)
cv2.waitKey(0)
代码解释:
- findContours :提取目标轮廓;
- approxPolyDP :对轮廓进行逼近,模拟逐步收缩;
- drawContours :绘制每次逼近后的轮廓,模拟骨架生成。
该方法简单直观,但容易受到噪声影响,需结合平滑处理或中值滤波进行优化。
3.3 细化操作的数学基础
细化(Thinning)是骨架提取的核心操作,其目标是将图像中目标区域逐渐“削薄”,直到只剩下骨架线。细化过程需满足拓扑不变性,即不能破坏图像的连通性和分支结构。
3.3.1 连续细化与离散细化的对比
| 特性 | 连续细化 | 离散细化 |
|---|---|---|
| 数学基础 | 基于连续空间中的距离与曲率 | 基于离散像素空间 |
| 实现方式 | 使用微分方程或几何变形 | 使用像素级判断规则 |
| 应用场景 | 理论研究、连续模型分析 | 实际图像处理、工程应用 |
连续细化更适用于理论研究,而离散细化是实际图像处理中常用的方法。例如,Hilditch算法、Zhang-Suen算法等均属于离散细化方法。
3.3.2 拓扑保持的判定准则
细化过程中,必须确保不会破坏图像的拓扑结构。常见的拓扑保持判定准则包括:
- 连通性保持 :删除像素后,目标区域仍保持连通;
- 孔洞保持 :删除像素不应导致新的孔洞产生或原有孔洞消失;
- 端点保持 :不删除端点像素,避免骨架断裂;
- 非孤立点删除 :删除的像素应至少有两个相邻前景点。
例如,在Zhang-Suen细化算法中,对每个像素点 $ p $,判断其是否满足以下条件:
- $ p $ 是前景点;
- $ p $ 的邻接点数量在2到6之间;
- $ p $ 的邻接点中存在至少一个背景点;
- $ p $ 的邻接点变化次数为1。
这些规则确保了细化过程中的拓扑不变性。
3.4 骨架提取的质量评估
骨架提取的质量直接影响后续图像处理的效果。因此,必须建立合理的评估标准来衡量骨架的质量。
3.4.1 骨架连通性评估
骨架连通性是指骨架线是否保持完整的连接结构,没有断裂或孤立点。评估方法包括:
- 路径追踪法 :从骨架线的任意起点出发,能否遍历所有骨架点;
- 连通区域统计 :统计骨架图像中连通区域的数量,理想情况下应为1(单目标)。
代码示例(连通区域统计) :
import cv2
skeleton = cv2.imread('skeleton_image.png', 0)
num_labels, labels = cv2.connectedComponents(skeleton)
print(f'Number of connected components: {num_labels}')
3.4.2 骨架线的细度与准确性
骨架线应保持单像素宽度,同时准确位于目标区域的几何中心。评估指标包括:
| 指标 | 描述 |
|---|---|
| 细度 | 统计骨架线的最大宽度是否为1像素 |
| 准确性 | 计算骨架线与理想中心线的欧氏距离均值 |
| 分支数量 | 检测骨架线的分叉点数量,避免过多分支 |
示例代码(细度检测) :
import cv2
import numpy as np
skeleton = cv2.imread('skeleton_image.png', 0)
kernel = np.ones((3, 3), np.uint8)
dilated = cv2.dilate(skeleton, kernel, iterations=1)
width = cv2.absdiff(dilated, skeleton)
mean_width = np.mean(width)
print(f'Average width of the skeleton: {mean_width:.2f} pixels')
逻辑分析:
- 使用膨胀操作模拟骨架线的“加粗”;
- 计算膨胀后与原骨架的差值图像;
- 差值图像的平均灰度值反映了骨架线的宽度;
- 理想情况下,骨架线宽度应接近1像素,均值应在1.0左右。
通过上述章节的深入分析,我们可以看到,骨架提取不仅依赖于数学理论的支撑,也离不开具体算法的实现与优化。在下一章中,我们将深入探讨 Hilditch 算法的实现细节与优化策略。
4. Hilditch算法设计与实现
Hilditch算法是图像细化领域中最具代表性的串行细化算法之一,由T. Y. Hilditch于1970年代提出。该算法通过逐次删除边界像素来逐步提取图像的骨架线,同时确保图像的拓扑结构不被破坏。Hilditch算法在保持骨架连通性和细度方面具有良好的性能,广泛应用于字符识别、手写体识别和图像骨架化等领域。
4.1 Hilditch算法的基本原理
4.1.1 算法流程概述
Hilditch算法的核心思想是基于一个迭代删除机制,在每次迭代中对图像中的前景像素(值为1)进行判断,决定是否可以安全删除而不影响图像的拓扑结构。该算法主要分为两个阶段:
- 阶段一(Pass 1) :从左上角开始,逐行扫描图像,删除满足特定条件的像素。
- 阶段二(Pass 2) :从右下角开始反向扫描图像,继续删除满足另一组条件的像素。
这两个阶段交替进行,直到图像不再发生变化,即没有像素可以被删除为止。
4.1.2 判断条件与迭代策略
Hilditch算法定义了四组判断条件,用于决定某个像素是否可以被删除:
- C1 :像素点为前景像素(值为1)。
- C2 :像素点的邻域中有至少两个前景像素,且不超过六个前景像素。
- C3 :像素点的邻域中至少有1个背景像素(值为0)。
- C4 :删除该像素不会导致图像连通性被破坏。
这四个条件共同确保了在删除像素时不会破坏图像的骨架结构。算法的迭代策略采用交替扫描方向的方式,以避免局部最优和陷入死循环。
4.2 算法的伪代码实现
4.2.1 图像扫描策略
Hilditch算法采用交替方向扫描的方式进行迭代处理。伪代码如下:
repeat
changed = false
for each pixel in image (扫描方向:左上到右下)
if 满足删除条件C1~C4
标记该像素为待删除
删除所有标记的像素
if 有像素被删除
changed = true
for each pixel in image (扫描方向:右下到左上)
if 满足另一组删除条件
标记该像素为待删除
删除所有标记的像素
if 有像素被删除
changed = true
until not changed
4.2.2 像素点状态判断规则
Hilditch算法在判断像素是否可以删除时,需要检查其8邻域(3×3邻域)内的像素值。定义邻域如下:
P1 P2 P3
P8 P0 P4
P7 P6 P5
其中P0为当前像素,其余为邻域像素。算法判断条件如下:
- A :2 ≤ N(P0) ≤ 6(N(P0)表示P0邻域中前景像素的个数)
- B :T(P0) = 1(T(P0)表示邻域中从前景到背景的变化次数)
- C :P2 × P4 × P6 = 0 或者 P4 × P6 × P8 = 0(用于阶段一)
- D :P2 × P4 × P8 = 0 或者 P2 × P6 × P8 = 0(用于阶段二)
只有同时满足A、B和C或D的像素才能被删除。
4.3 算法的编程实现
4.3.1 VC++环境下的图像读取与显示
在VC++环境下,我们可以使用OpenCV库来读取和显示图像。以下是一个图像读取与显示的示例代码:
#include <opencv2/opencv.hpp>
using namespace cv;
int main() {
Mat src = imread("input.png", IMREAD_GRAYSCALE);
threshold(src, src, 128, 1, THRESH_BINARY); // 二值化为0和1
imshow("Original Image", src * 255); // 显示原始图像
waitKey(0);
return 0;
}
代码逻辑分析:
-
imread函数读取灰度图像; -
threshold函数将图像二值化为0和1; -
imshow函数显示图像; -
waitKey(0)保持窗口显示。
4.3.2 二维数组表示图像数据
在实现Hilditch算法时,我们通常将图像表示为二维数组。以下是一个图像数据结构的定义和初始化方式:
int width = src.cols;
int height = src.rows;
int** img = new int*[height];
for (int i = 0; i < height; ++i) {
img[i] = new int[width];
for (int j = 0; j < width; ++j) {
img[i][j] = (int)src.at<uchar>(i, j);
}
}
代码逻辑分析:
- 使用
new动态分配二维数组; - 将图像每个像素值(0或255)转换为0或1;
-
img[i][j]表示第i行第j列的像素值。
4.4 算法优化与边界处理
4.4.1 边界像素的特殊处理
在Hilditch算法中,图像的边界像素由于邻域不完整,容易出现误删或漏删的情况。为了提高算法的鲁棒性,我们可以在处理边界像素时做以下优化:
- 零填充(Zero Padding) :在图像周围添加一圈0值像素,使边界像素也能完整访问其8邻域。
- 边缘检测预处理 :在细化前先提取图像边缘,减少边界像素的误删。
// 添加零填充
int padWidth = width + 2;
int padHeight = height + 2;
int** paddedImg = new int*[padHeight];
for (int i = 0; i < padHeight; ++i) {
paddedImg[i] = new int[padWidth];
for (int j = 0; j < padWidth; ++j) {
if (i == 0 || i == padHeight - 1 || j == 0 || j == padWidth - 1) {
paddedImg[i][j] = 0; // 边界填充0
} else {
paddedImg[i][j] = img[i - 1][j - 1];
}
}
}
代码逻辑分析:
- 新建一个尺寸为
padHeight x padWidth的数组; - 图像边界填充为0;
- 中间区域复制原图像数据。
4.4.2 算法执行效率提升策略
Hilditch算法由于需要多次迭代扫描图像,计算量较大。为了提升效率,可以采取以下策略:
- 提前终止迭代 :当某次迭代中没有像素被删除时,直接终止算法;
- 使用标记数组 :避免重复访问图像数据;
- 并行化扫描 :在现代CPU/GPU上并行处理图像像素;
- 稀疏矩阵优化 :只处理前景像素,跳过背景像素。
以下是一个使用标记数组优化的代码片段:
bool changed;
do {
changed = false;
bool** mark = new bool*[height];
for (int i = 0; i < height; ++i) {
mark[i] = new bool[width];
memset(mark[i], 0, width);
}
for (int i = 1; i < height - 1; ++i) {
for (int j = 1; j < width - 1; ++j) {
if (paddedImg[i][j] == 1 && checkDeleteConditions(paddedImg, i, j)) {
mark[i][j] = true;
changed = true;
}
}
}
// 删除标记的像素
for (int i = 1; i < height - 1; ++i) {
for (int j = 1; j < width - 1; ++j) {
if (mark[i][j]) {
paddedImg[i][j] = 0;
}
}
}
// 释放标记数组
for (int i = 0; i < height; ++i) delete[] mark[i];
delete[] mark;
} while (changed);
代码逻辑分析:
- 使用
mark数组记录需要删除的像素; - 只在标记后统一删除,避免重复扫描;
- 提高执行效率,减少内存访问冲突。
表格:Hilditch算法与MAT算法对比
| 特性 | Hilditch算法 | Medial Axis Transform (MAT) |
|---|---|---|
| 处理方式 | 串行删除像素 | 基于距离变换 |
| 骨架连续性 | 保持较好 | 保持较好 |
| 细度 | 1像素宽 | 通常1像素宽 |
| 计算复杂度 | O(n²)(n为图像尺寸) | O(n² log n) |
| 适用场景 | 文字、图形细化 | 医学图像、复杂结构 |
| 实现难度 | 中等 | 较高 |
Mermaid流程图:Hilditch算法执行流程
graph TD
A[读取图像] --> B[二值化处理]
B --> C[添加零填充]
C --> D[初始化标记数组]
D --> E[第一阶段扫描]
E --> F{满足删除条件?}
F -- 是 --> G[标记删除像素]
F -- 否 --> H[继续扫描]
G --> I[第二阶段扫描]
I --> J{满足另一组条件?}
J -- 是 --> K[删除像素]
J -- 否 --> L[继续扫描]
K --> M{是否有像素被删除?}
M -- 是 --> E
M -- 否 --> N[输出骨架图像]
通过本章的详细讲解,读者应已掌握Hilditch算法的设计原理、实现步骤以及优化策略。下一章我们将介绍Medial Axis Transform(MAT)算法的实现方法,并对比其与Hilditch算法的异同。
5. Medial Axis Transform (MAT) 算法实现
5.1 MAT算法的基本思想
Medial Axis Transform(MAT),即中轴变换,是一种基于距离变换的骨架提取方法。其核心思想是将图像中每个前景像素点视为某个最大内切圆的圆心,这些圆心的集合构成了图像的骨架结构。
5.1.1 基于距离变换的骨架提取
MAT算法依赖于距离变换(Distance Transform),即为每个前景像素计算其到最近背景像素的距离。通过找到距离变换图像中的局部最大值点,即可获得图像的中轴线。这些局部最大值点代表了图像形状的“脊梁”,是骨架提取的关键。
数学表达为:
对于一幅二值图像 $ I(x,y) $,若 $ I(x,y) = 1 $ 表示前景像素,$ I(x,y) = 0 $ 表示背景像素,则距离变换定义为:
D(x, y) = \min_{(u,v) \in B} \sqrt{(x - u)^2 + (y - v)^2}
其中 $ B $ 是所有背景像素集合。
5.1.2 最大圆盘中心点的判定
在完成距离变换后,MAT算法的核心步骤是识别出图像中每个像素点是否为局部最大值。局部最大值的定义是:该点的值大于其邻域内所有点的值。
在二维图像中,通常采用4邻域或8邻域判断局部最大值。例如,在8邻域中,某点 $ (x,y) $ 的值如果大于其周围8个点的值,则认为该点为局部最大值点。
5.2 距离变换的实现方法
5.2.1 欧式距离与曼哈顿距离比较
在MAT算法中,距离变换可以使用不同的距离度量方式,常见的是欧式距离(Euclidean Distance)和曼哈顿距离(Manhattan Distance):
| 距离类型 | 定义公式 | 特点 |
|---|---|---|
| 欧式距离 | $ d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $ | 精确度高,计算量大,适合高质量骨架提取 |
| 曼哈顿距离 | $ d = | x_1 - x_2 |
在实际实现中,欧式距离更常用于精确的骨架提取,而曼哈顿距离则用于快速原型开发或性能优先的场景。
5.2.2 快速距离变换算法
为了提升计算效率,通常采用 并行距离变换算法(如Borgefors算法) ,其核心思想是分两趟扫描图像(从左上到右下,再从右下到左上),在每趟扫描中更新每个像素的距离值。
伪代码如下:
# 快速距离变换(欧式)伪代码
def distance_transform(image):
height, width = image.shape
dt = np.zeros((height, width), dtype=np.float32)
# 初始化距离图
for i in range(height):
for j in range(width):
if image[i][j] == 0: # 背景点
dt[i][j] = 0
else:
dt[i][j] = np.inf
# 第一趟扫描(从左上到右下)
for i in range(height):
for j in range(width):
if image[i][j] == 1:
if i > 0 and j > 0:
dt[i][j] = min(dt[i][j], dt[i-1][j-1] + sqrt(2))
if i > 0:
dt[i][j] = min(dt[i][j], dt[i-1][j] + 1)
if j > 0:
dt[i][j] = min(dt[i][j], dt[i][j-1] + 1)
# 第二趟扫描(从右下到左上)
for i in reversed(range(height)):
for j in reversed(range(width)):
if image[i][j] == 1:
if i < height - 1 and j < width - 1:
dt[i][j] = min(dt[i][j], dt[i+1][j+1] + sqrt(2))
if i < height - 1:
dt[i][j] = min(dt[i][j], dt[i+1][j] + 1)
if j < width - 1:
dt[i][j] = min(dt[i][j], dt[i][j+1] + 1)
return dt
5.3 MATLAB与OpenCV中的实现
5.3.1 OpenCV库函数的使用
OpenCV提供了内置的 distanceTransform 函数用于快速实现距离变换:
#include <opencv2/opencv.hpp>
int main() {
cv::Mat src = cv::imread("input.png", 0); // 读取图像
cv::Mat binary;
cv::threshold(src, binary, 128, 255, cv::THRESH_BINARY); // 二值化处理
cv::Mat dist;
cv::distanceTransform(binary, dist, cv::DIST_L2, 5); // 欧式距离变换
cv::Mat skeleton;
cv::normalize(dist, skeleton, 0, 1, cv::NORM_MINMAX); // 归一化显示
cv::imshow("Distance Transform", skeleton);
cv::waitKey(0);
return 0;
}
5.3.2 OpenCV图像数据结构转换
在使用OpenCV进行图像处理时,需要注意图像数据类型的转换:
-
CV_8UC1:8位单通道图像(适合原始图像) -
CV_32FC1:32位浮点型单通道图像(适合距离图)
示例:将距离图转换为局部最大值图(骨架提取):
cv::Mat local_max;
cv::dilate(dist, local_max, cv::Mat()); // 膨胀操作获取邻域最大值
cv::compare(dist, local_max, local_max, cv::CMP_EQ); // 比较获取局部最大值点
cv::bitwise_and(binary, local_max, skeleton); // 结合二值图保留骨架
5.4 细化算法的完整流程整合
5.4.1 算法流程的模块化设计
MAT算法的完整流程可以分为以下几个模块:
graph TD
A[输入图像] --> B[图像预处理]
B --> C[二值化处理]
C --> D[距离变换]
D --> E[局部最大值检测]
E --> F[骨架提取]
F --> G[结果输出]
模块化设计使得算法结构清晰,便于调试和优化。
5.4.2 图像处理与结果输出的整合实现
将上述模块整合成一个完整的MAT算法实现:
import cv2
import numpy as np
def mat_skeletonize(image_path):
# 1. 读取图像并二值化
img = cv2.imread(image_path, 0)
_, binary = cv2.threshold(img, 128, 255, cv2.THRESH_BINARY)
# 2. 距离变换
dist = cv2.distanceTransform(binary, cv2.DIST_L2, 5)
# 3. 局部最大值检测
local_max = cv2.dilate(dist, None)
skeleton = (dist == local_max) & (binary.astype(bool))
# 4. 转换为图像格式输出
result = (skeleton * 255).astype(np.uint8)
cv2.imshow("MAT Skeleton", result)
cv2.waitKey(0)
cv2.destroyAllWindows()
# 调用函数
mat_skeletonize("input.png")
此实现完整地展示了从图像输入到骨架提取的整个流程,具有良好的可扩展性和可移植性。
简介:细化算法是图像处理中的关键技术,主要用于提取二值黑白图像的骨架,实现物体形状的紧凑表示。该技术广泛应用于模式识别、图像分析和生物医学图像处理等领域。本文项目基于VC++平台,采用C++语言实现细化算法,包含Hilditch算法、Medial Axis Transform(MAT)、迭代腐蚀与膨胀等多种主流细化方法。项目资源中包含详细代码和说明文档,帮助开发者掌握细化算法的核心实现过程,并提升图像处理实战能力。





















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








