Mathematica 显示连分数的4种方法

Mathematica 显示连分数的4种方法

实数的连分数展开

连分数可用来方便地得到对无理数的优异的有理数逼近。例如$\pi$的连分数表示形式为

$$\pi =3+\frac{1}{7+\frac{1}{15+\frac{1}{1+\frac{1}{292+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{2+\frac{1}{1+\dots }}}}}}}}}$$

可记为$[3;7,15,1,292,1,1,1,2,1,\cdots ]$。

截取其前2项及前3项分别为 $3+\frac{1}{7}=\frac{22}{7}$和$3+\frac{1}{7+\frac{1}{15}}=\frac{333}{106}$，正是祖冲之得到的约律$\frac{22}{7}$和密率$\frac{333}{106}$。

那么，怎样得到连分数中的整数序列呢？

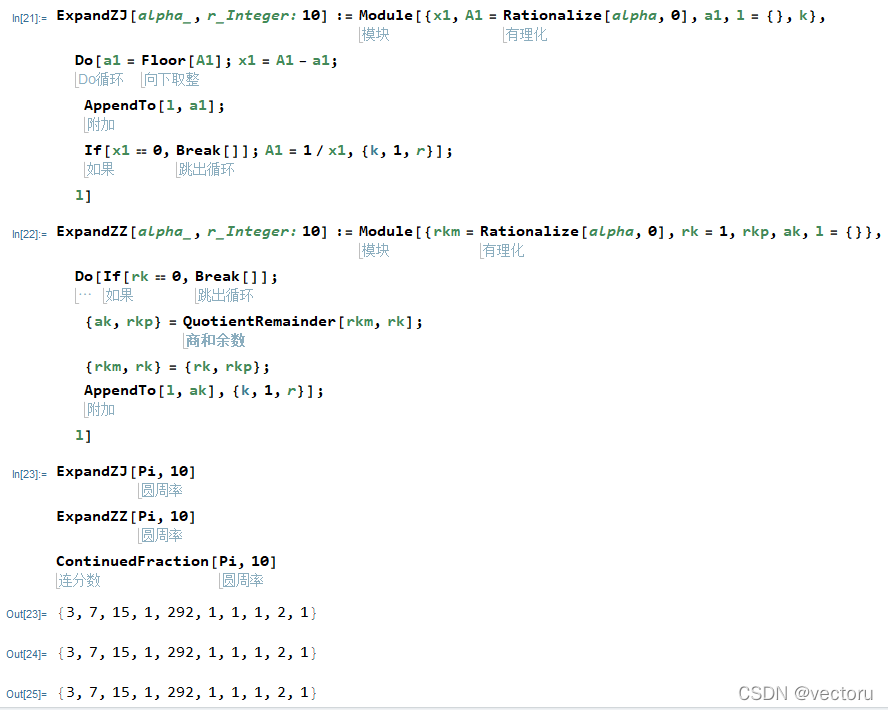
可以通过直接展开法¹：

ExpandZJ[alpha_,r_Integer:10]:=Module[
	{x1,A1=Rationalize[alpha,0],a1,l={},k},
	Do[
		a1=Floor[A1];x1=A1-a1;
		AppendTo[l,a1];
		If[x1==0,Break[]];A1=1/x1,
		{k,1,r}
	];
	l
]

注意，用计算机计算时，alpha需被转化为有理数进行运算，因为浮点数的精度问题导致迭代几次后数值不准。

也可以通过辗转相除法¹：

ExpandZZ[alpha_,r_Integer:10]:=Module[
	{rkm=Rationalize[alpha,0],rk=1,rkp,ak,l={}},
	Do[
		If[rk==0,Break[]];
		{ak,rkp}=QuotientRemainder[rkm,rk];
		{rkm,rk}={rk,rkp};
		AppendTo[l,ak],
		{k,1,r}
	];
	l
]

不过作为世界三大数学软件之一，Mathematica内置了连分数展开的函数，即用ContinuedFraction[x,n]生成 x 的连分数表示中前 n 项的列表。这三个函数运行如下：

计算连分数的值

有限连分数的形式表明它的计算方法是由下向上的，即对于$a+\frac{1}{b+\frac{1}{c+\frac{1}{d}}}$，我们先计算$c+\frac{1}{d}$，再计算$b+\frac{1}{(c+\frac{1}{d})}$，最后计算$a+\frac{1}{(b+\frac{1}{c+\frac{1}{d}})}$。这可以看做一种“含参数”函数的迭代过程，即$f_a(f_b(f_c(d))))$，其中$f_i(x)=i+\frac{1}{x}$。或者看做$f(f(f(d,c),b),a)$，其中$f(x,i)=i+\frac{1}{x}$。对于一般的迭代，mma中的Nest函数可以实现，而对于这种“含参数”函数的迭代，mma中的FoldList函数恰好可以实现。

查阅mma的文档，我们可以得知：Fold[f, {d, c, b, a}]==f[f[f[d, c], b], a]

于是我们可以这样计算连分数：list = ContinuedFraction[Pi, 10]; Fold[#2 + 1/#1 &, Reverse@list]。
其中#2 + 1/#1 &表示一个纯函数，其意义相当于定义了f[x_,y_]:=y+1/x后的f。Reverse表示反转列表，因为如前所述，我们的计算是由下向上的。
实际运行如下：

显示连分数

在得到连分数中的整数序列后，下面来看看怎么显示连分数。
我们对整数的访问过程与上面的计算方法一样，不过要避免数字的计算。

1.String&Orderless

如果a=“1”,b=“1”,那么a+b的值输入mma后会得到"1+1"，但显示的效果不带引号，就好像它忘记了计算数字1+1。
我们可以设想，如果把每个整数加上引号变成字符串，那么分数就不会化简了²。实际操作一下：
Fold[(#2 + 1/#1) &, ToString /@ Reverse@ContinuedFraction[Pi, 10]]

发现连分数的效果有了，但是排列的并不美观。猜测与表达式的排序有关（它自动忽略了加法的顺序，当然加法默认没有顺序）。不过可以清除Plus的无序属性来取消它的自行排列。当然清除后建议立刻恢复，否则输入a + b + a的结果将原封不动地返回，而不是2 a + b。如果要从显示的连分数恢复成化简后的分数，需要将所有的字符串替换成它的表达式结果。这是代码实现及效果：

ClearAttributes[Plus, Orderless]
Fold[(#2 + 1/#1) &, ToString /@ Reverse@ContinuedFraction[Pi, 10]]
% /. x_String :> ToExpression[x]
SetAttributes[Plus, Orderless]

2.HoldForm

HoldForm保持表达式不计算的形式，恢复计算则需要ReleaseHold //@expr。

Fold[#2 + 1/HoldForm[#] &, Reverse@ContinuedFraction[Pi, 10]]
ReleaseHold //@ %

3.Inactivate

Inactivate使Plus失效，恢复只需要Activate作用。

Fold[Inactivate[#2 + 1/#1, Plus] &, Reverse@ContinuedFraction[Pi, 10]]
Activate[%]

4.Defer

Defer(推迟计算)，只有当表达式显式地输入时才计算，而恢复则需要复制结果后直接输入。

Fold[#2 + 1/Defer[#1] &, Reverse@ContinuedFraction[Pi, 10]]

写在最后

以上四种方法中，个人比较喜欢HoldForm实现的。因为听群里大神说mma中字符串效率比Inactive低很多。而Inactive实现的结果中加号的颜色变暗了，且最后一个分数中分母是1时，没显示成1/1。Defer的话，还要再手动复制输入一遍，程序处理中显得不方便。实际上，HoldForm(还有Inactive)加的位置也是多次尝试出来的，读者可以试试Fold[#2 + HoldForm[1/#1] &, Reverse@ContinuedFraction[Pi, 10]]，其显示末尾的“1×1/1”，并不好看，也不知原因(欢迎补充)。

显示连分数原本是数学实验作业中遇到的问题，本文中四种方法的(貌似)中间两种是在mma群里询问大佬们才得知的。当年迎难而上，精益求精，可今非昔比，岁月蹉跎，感慨万千。

最后，送给大家给大家准备一个连分数：
5+1/(4+1/(1+1/(29+1/(1+1/(1+1/(1+1/(3+1/(1+1/(2+1/(1+1/(2+1/(1+1/(1+1/9)))))))))))))，它是由某个小数填入代码
Fold[#2 ~~ "+1/(" ~~ #1 ~~ ")" &, ToString /@ Reverse@ContinuedFraction[Rationalize[1.42857, 0]]]中1.42857的位置得到的，至于该小数是多少，大家一算便知[滑稽]。

---

1. 李尚志《数学实验》 ↩︎ ↩︎

2. Mathematica基础——处理连分数问题-百度经验 https://jingyan.baidu.com/article/7c6fb42821117b80642c90f3.html ↩︎