树(Tree)——(一)基础知识

目录

关于树的术语 

儿子兄弟链式表示法

二叉树概念和基本特征 

二叉树的形态

前序、中序、后序遍历特性

                  习题梳理：

---

 

---

树存在的主要意义就是为了方便查找，如二叉树就有二分的思想。

 

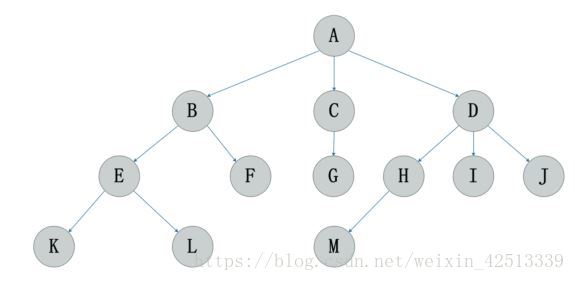
关于树的术语 

1.结点的度(Degree)：结点的子树个数。   （例如上面的图中A有三个节点，那么A的度为3）

2.树的度：树的所有结点中最大的度数。    （上图树的度为3）

3.叶结点( Leaf)： 度为0的结点。

4.父结点( Parent)：有子树的结点是其子树的根结点的父结点。 

5.子结点( Child)：若A结点是B结点的父结点，则称B结点是A结点的子结点；子结点也称孩子结点。

6.兄弟结点( Sibling)：具有同一父结点的各结点彼此是兄弟结点。 

7.祖先结点(Ancestor)：沿树根到某一结点路径上的所有结点都是这个结点的祖先结点。 

8.子孙结点(Descendant)：某一结点的子树中的所有结点是这个结点的子孙。 

9.结点的层次( Level)：规定根结点在1层，其它任一结点的层数是其父结点的层数加1。 

10.树的深度( Depth) ：树中所有结点中的最大层次是这棵树的深度。 

 

儿子兄弟链式表示法

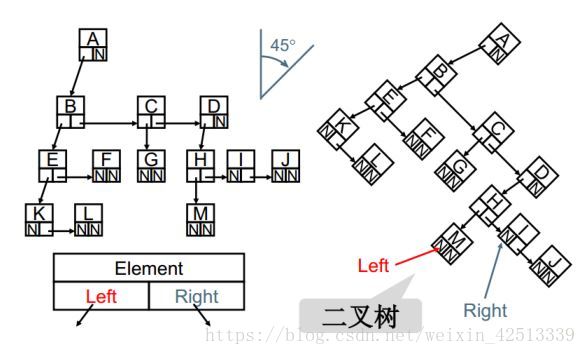
如上图所示，这几步经历了从 多叉树 变成 二叉树 的过程。

这个方法形成了二叉树，实现了节点和结构的统一。

 

二叉树概念和基本特征 

二叉树包含左右子树，左右子树可为空，而且只有左右子树也可以，下面均是二叉树。

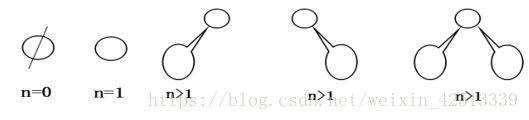
基本特征包括

1.每个结点最多只有两棵子树(不存在度大于2的结点)；

2.二叉树的子树，有左右之分，左子树和右子树次序不能颠倒。所以下面是两棵不同的树。 

 

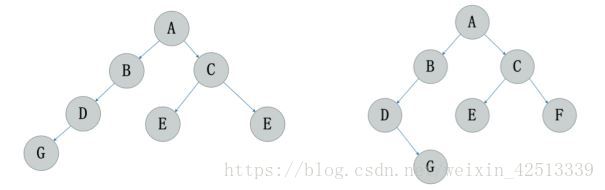
二叉树的形态

1.普通二叉树（如上面图中的就是）

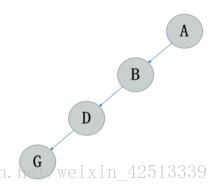
2.斜二叉树 （实质也是链表，所以对于二叉树，这种树是用不到的）

 

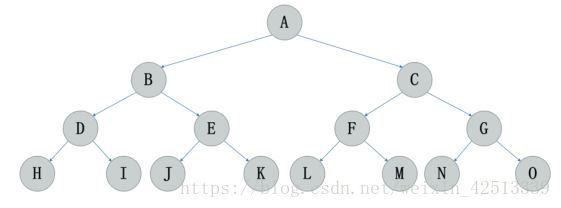
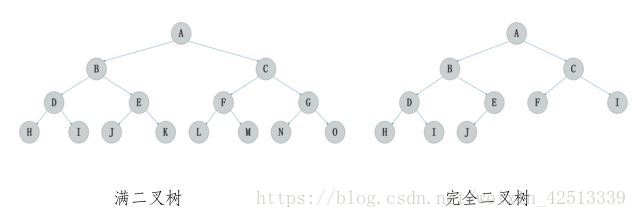
3.满二叉树 ：如果所有分支结点都存在左子树和右子树，并且所有叶子结点都在同一层上，这样的二叉树称为满二叉树。 

 

4.完全二叉树 ：如果一棵深度为k，有n个结点的二叉树中各结点能够与深度为k的顺序编号的满二叉树从1到n标号的结点相对应的二叉树称为完全二叉树。（ 换句话说，完全二叉树从根结点到倒数第二层满足完美二叉树，最后一层可以不完全填充，其叶子结点都靠左对齐。）

5.完满二叉树：所有非叶子结点的度都是2。（只要你有孩子，你就必然是有两个孩子。）

 

前序、中序、后序遍历特性

前序遍历	中序遍历	后序遍历
1.访问根节点   2.前序遍历左子树   3.前序遍历右子树	1.中序遍历左子树   2.访问根节点  3.中序遍历右子树	1.后序遍历左子树   2.后序遍历右子树  3.访问根节点
可以记为根左右，若二叉树为空，则结束返回。	可以记为左根右	记为左右根

这里的遍历，是遍历到哪一个点，然后对这个继续求遍历。（本质就是递归）

举例：

拿下图的左边的题来说。它求中序的步骤是：第一步对于节点 A 的"左根右"，就是到了 D 这个点，然后立马对 D 这个点中序遍历 "左根右"，由于D没有左，所以输出 D 这个‘根’，所以第一个输出D。然后到‘右’，就是 E 点，由于 E 没有子节点，所以不用遍历 E ，直接输出就可以。

现在输出了 D - E .

回到之前的‘根’ A 节点，左边遍历完，根据"左根右"，所以输出‘根’  A 。然后到了‘右’，这就是 B ，立马对 B 继续遍历，得到 C 节点，根据"左根右"，没有‘左’，输出‘根’，就是 C ，然后是‘右’ 节点 F 。

这样我们输出了 D - E - A - C - F ,最后就是‘右’节点 B 了。这样中序就是 D - E - A - C - F - B .

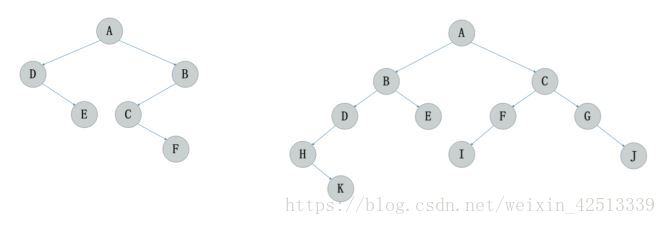
我们可以用上面相似的方法，求前中后序。

上面两图的答案分别是：

	左边	右边
先序	A - D - E - B - C - F	A - B - D - H - K - E - C - F - I - G - J
中序	D - E - A - C - F - B	H - K - D - B - E - A - I - F - C - G - J
后序	E - D - F - C - B - A	K - H - D - E - B - I - F - J - G - C - A

 

习题梳理：

直接上题：

1.有如下两种遍历方式，请写出第三种遍历方式并画图 。(考研题)

（1）

先序遍历结果：A  B  D  H  K  E  C  F  I  G  J 
中序遍历结果：H  K  D  B  E  A  I  F  C  G  J 

思路：从先序可以知道 A 是根节点，所以我们可以从中序的结果反推出（H K D B E    A       I F C G J）得到 H K D B E在左节点， I F C G J在右节点。然后根据先序的B D H K E 我们可以知道，B是中间节点，利用中序同样可以得到B的左节点和右节点，依次操作我们便能得到树的图

（2）

中序遍历结果：B D C E A F H G 
后序遍历结果：D E C B H G F A 

思路：主要还是要靠中序结果，因为后序遍历是"左右根"，所以最后一个节点就是根节点，为 A ，然后我们就能从中序，得到 A 的左右节点。然后再根据后序 D E C B ，我们知道 B 就是根节点，根据中序得知  D C E 都在右节点上，根据后序的”左右根“，说明 C 是 D E C 的根节点，再根据中序的D C E 的顺序，就能得知，D是 C 的左节点，E 是右节点。

 

总结：知两者可求第三者，必须是先中求后，或者后中求先。

比如：满足先序: AB   后序:BA，那么树是不唯一的。