目录
- 1 前言
- 2 回归的评估指标
- 2.1 均方误差 ( MSE,Mean Squared Error)
- 2.2 均方根误差(RMSE,Root Mean Square Error)
- 2.3 平均绝对误差(MAE,Mean Absolute Error)
- 2.4 平均绝对百分比误差 (MAPE,Mean Absolute Percentage Error)
- 2.5 对称平均绝对百分比误差(SMAPE, Symmetric Mean Absolute Percentage Error)
- 2.6 R平方(R², Coefficient of Determination)
- 2.7 调整后的R平方(Adjusted R²)
- 2.8 平均平方对数误差 ( MSLE,Mean Squared Logarithmic Error)
- 2.9 均方根对数误差 (RMSLE,Root Mean Squared Logarithmic Error)
- 2.10 最大误差 (Max Error)
- 2.11 中位数绝对误差 (Median Absolute Error, MedAE)
- 3 分类的评估指标
- 4 总结
- 参考学习
1 前言
对于机器学习模型,评价模型的好坏是十分重要的一环,不同的任务对应的评估指标也有所差异,以更好的评价和比较模型的优劣。诸如分类(classification)、回归(regression)、排序(ranking)、聚类(clustering)、主题模型(topic modeling)等。本文则对不同场景的评估指标进行总结梳理1。
碎碎语:最近书籍看的有点乱,各方面都在涉及,极大地分散了精力,导致对各方面了解的都不够细致,该理理头绪,排排顺序学习了
2 回归的评估指标
回归模型的输出是连续型的数值。常用的评估指标包括:
- 均方误差 ( MSE,Mean Squared Error)
- 均方根误差 (RMSE,Root Mean Squared Error)
- 平均绝对误差(MAE,Mean Absolute Error)
- 平均绝对百分比误差 (MAPE,Mean Absolute Percentage Error)
- 对称平均绝对百分比误差(SMAPE, Symmetric Mean Absolute Percentage Error)
- 决定系数,R平方(R², Coefficient of Determination)
- 调整后的R² (Adjusted R²)
- 平均平方对数误差 ( MSLE,Mean Squared Logarithmic Error)
- 均方根对数误差 (RMSLE,Root Mean Squared Logarithmic Error)
- 最大误差 (Max Error)
- 中位数绝对误差 (Median Absolute Error, MedAE)
2.1 均方误差 ( MSE,Mean Squared Error)
均方误差:计算模型预测值与真实值之间差异的平方的平均值。
M S E = ∑ ( y i − y ^ i ) 2 n MSE=\frac{\sum(y_i - \hat y_i)^2}{n} MSE=n∑(yi−y^i)2
其中, y i y_i yi是第i个样本的真实值, y ^ i \hat y_i y^i是第i个样本的预测值,n是样本的个数。
优点:
- 容易计算和理解
- 对大误差更加敏感,适合希望模型对异常值敏感的情况。
缺点:
- 量纲与原始数据不同,不便于解释
- 容易受到离群值的影响,对异常值敏感
2.2 均方根误差(RMSE,Root Mean Square Error)
均方根误差:计算所有的预测值与真实值偏差的平方之和的均值,再求平方根,即均方误差的平方根。
R M S E = M S E = ∑ ( y i − y ^ i ) 2 n RMSE = \sqrt{MSE} = \sqrt{\frac{\sum(y_i - \hat y_i)^2}{n}} RMSE=MSE=n∑(yi−y^i)2
其中, y i y_i yi是第i个样本的真实值, y ^ i \hat y_i y^i是第i个样本的预测值,n是样本的个数。
优点:与MSE相比,RMSE具有与原始数据相同的单位,因此更容易解释。
缺点:容易受到离群值的影响,对异常值比较敏感。
2.3 平均绝对误差(MAE,Mean Absolute Error)
平均绝对误差:计算预测值与真实值之间差异的绝对值的平均值。
M A E = ∑ ( ∣ ( y i − y ^ i ) ∣ ) n MAE= \frac{\sum(\vert{(y_i - \hat y_i)}\vert)}{n} MAE=n∑(∣(yi−y^i)∣)
优点:
- 对离群值的敏感度较低,更为稳健,适用于噪声较大的数据集
- 量纲与原始数据一致,便于解释。
缺点:
- MAE在优化时的梯度信息不如MSE明确,可能导致收敛速度较慢。
- 不惩罚大误差,适合误差分布较为均匀的情况。
2.4 平均绝对百分比误差 (MAPE,Mean Absolute Percentage Error)
平均绝对百分比误差:预测值与实际值之间的绝对误差相对于实际值的百分比。
M A P E = ∑ ∣ ( y i − y ^ i ) y i ∣ n ∗ 100 MAPE=\frac{\sum\vert{\frac{(y_i - \hat y_i)}{y_i}}\vert}{n}*100 MAPE=n∑∣yi(yi−y^i)∣∗100
优点:无量纲,便于跨数据集比较。
缺点:
- 当实际值接近零时,MAPE 会变得非常大,数值不稳定。
- 不适用于实际值为零或接近零的情况。
2.5 对称平均绝对百分比误差(SMAPE, Symmetric Mean Absolute Percentage Error)
对称平均绝对百分比误差:SMAPE 是对MAPE的改进,避免了对实际值接近零时的不稳定性。
S M A P E = 1 n ∑ ∣ y i − y ^ i ∣ ( ∣ y i ∣ + ∣ y ^ i ∣ ) / 2 ∗ 100 SMAPE=\frac{1}{n}\sum{\frac{\vert{y_i-\hat y_i}\vert}{(\vert{y_i}\vert+\vert{\hat y_i}\vert)/2}}*100 SMAPE=n1∑(∣yi∣+∣y^i∣)/2∣yi−y^i∣∗100
优点:对实际值接近零的情况更加稳健。
缺点:计算较为复杂。
2.6 R平方(R², Coefficient of Determination)
R平方(R²):表示模型解释的方差占总方差的比例,取值范围在0到1之间。R² 越接近1,模型的解释能力越强。
R 2 = 1 − ∑ ( y i − y ^ i ) 2 ∑ ( y i − y ˉ ) 2 R^2=1-\frac{\sum{(y_i-\hat y_i)^2}}{\sum{(y_i-\bar y)^2}} R2=1−∑(yi−yˉ)2∑(yi−y^i)2
优点:易于解释,表示模型对数据的拟合程度。
缺点:
- 当新特征加入时,R² 可能不会下降,甚至可能增加,即使这些特征对模型没有帮助。
- 对于数据量较小的样本,R² 可能不稳定。
2.7 调整后的R平方(Adjusted R²)
调整后的R平方(Adjusted R²):调整后的R² 考虑了模型中特征的数量,避免盲目增加特征导致R² 虚高。
A d j u s t e d R 2 = 1 − ( 1 − R 2 ) ( n − 1 ) n − k − 1 Adjusted \hspace{3pt} R^2=1-\frac{(1-R^2)(n-1)}{n-k-1} AdjustedR2=1−n−k−1(1−R2)(n−1)
优点:能够避免过拟合,对于特征多的模型更加公平。
缺点:计算相对复杂。
2.8 平均平方对数误差 ( MSLE,Mean Squared Logarithmic Error)
平均平方对数误差 :对输出取对数后的均方误差。
优点:
- 适用于目标值范围跨度大的情况。
- 减少大误差的影响。
缺点:目标值需要为正数。
2.9 均方根对数误差 (RMSLE,Root Mean Squared Logarithmic Error)
均方根对数误差:MSLE的平方根。
优点:单位与对数变换后的单位一致,可能更直观。
缺点:同MSLE,目标值需为正数。
2.10 最大误差 (Max Error)
最大误差 (Max Error):所有样本中最大的预测误差。
优点:直观反映模型可能犯下的最大错误。
缺点:只关注最坏情况,可能不反映整体性能。
2.11 中位数绝对误差 (Median Absolute Error, MedAE)
中位数绝对误差 (Median Absolute Error, MedAE):测误差的中位数绝对值。
优点:对异常值不敏感,因为使用中位数。
缺点:不如均值敏感,可能无法反映整体误差。

3 分类的评估指标
分类模型的输出是离散的标签。常用的评估指标包括:
- 准确率(Accuracy)
- 平均类准确率(Per-class Accuracy)
- 精确率(Precision)
- 召回率(Recall)
- 平均类精确率、平均类召回率
- F1值(F1-Score)
- 混淆矩阵(Confusion Matrix)
- ROC曲线(Receiver Operating Characteristic Curve)
- AUC(Area under the Curve)
- 对数损失(Log Loss) / 交叉熵损失(Cross-Entropy Loss)
- 马修斯相关系数(Matthews Correlation Coefficient, MCC)
3.1 准确率(Accuracy)
准确率:模型预测分类正确的样本个数占总样本数的比例。
准确率 = 正确分类的样本个数 总样本数 = T P + T N T P + T N + F P + F N 准确率=\frac{正确分类的样本个数}{总样本数}=\frac{TP+TN}{TP+TN+FP+FN} 准确率=总样本数正确分类的样本个数=TP+TN+FP+FNTP+TN
优点:简单易懂,适用于类别分布均衡的场景。
缺点:当类别分布不均衡时,可能会产生误导(例如,少数类样本被忽略)。
3.2 平均类准确率(Per-class Accuracy)
平均类准确率:准确率的一个变形,指每个类别下的准确率,然后再计算它们的平均值。
- 准确率是宏观平均
- 平均类准确率则是一个微观的平均。
备注:
- 当某一个类别下的类别远多于另外的类别,准确率会给出一个扭曲的结果;
- 当某个类别的样本个数很少,那么造成该类的准确率的方差过大,该类的准确率的可靠性则要比其他类要差。
宏平均适用于类别分布均衡的场景,微平均适用于类别分布不均衡的场景。
3.3 精确率(Precision)
精确率:在模型预测为正类的样本中,实际为正类的比例。
P r e c i s i o n = T P T P + F P Precision=\frac{TP}{TP+FP} Precision=TP+FPTP
优点:关注模型预测的“准确性”,适用于需要减少误报的场景(如垃圾邮件检测)。
缺点:忽略了未被预测为正类的样本,可能低估了模型的性能。
3.4 召回率(Recall) / 真阳性率(True Positive Rate, TPR)
召回率:在实际为正类的样本中,模型正确预测为正类的比例。
R e c a l l = T P T P + F N Recall=\frac{TP}{TP+FN} Recall=TP+FNTP
优点:关注模型的“覆盖率”,适用于需要减少漏报的场景(如癌症检测)。
缺点:忽略了误报的情况,可能导致模型过于宽松。
3.5 平均类精确率、平均类召回率
平均类精确率、平均类召回率 和 精确率、召回率的关系,这一点和准确率和平均类准确率类似。
3.6 F1值(F1-Score)
F1值:精确率和召回率的调和平均值,综合考虑了模型的准确性和覆盖率。
F 1 = 2 × 精确率 × 召回率 精确率 + 召回率 F1=2 \times \frac{精确率\times召回率 }{精确率+召回率} F1=2×精确率+召回率精确率×召回率
优点:适用于类别分布不均衡的场景,尤其需要平衡精确率和召回率时。
缺点:仅考虑了正类的情况,未考虑负类的影响。
3.7 混淆矩阵
混淆矩阵:一个 n×n的矩阵,用于展示模型的分类结果。
- TP(True Positive): 正类样本被正确分类。
- FP(False Positive): 负类样本被错误分类为正类。
- FN(False Negative): 正类样本被错误分类为负类。
- TN(True Negative): 负类样本被正确分类。
优点:全面展示模型的分类结果,便于分析误差类型。
缺点:计算和解释相对复杂。
3.8 ROC曲线(Receiver Operating Characteristic Curve)
ROC曲线:ROC曲线是描述分类模型在不同阈值下,真阳性率(TPR)和假阳性率(FPR)的关系曲线。
- TPR(True Positive Rate): 同召回率。
- FPR(False Positive Rate): F P R = F P F P + T N FPR=\frac{FP}{FP+TN} FPR=FP+TNFP
优点:适用于类别分布不均衡的场景,能直观展示模型的分类能力。
缺点:需要手动选择分类阈值,计算较为复杂。
3.9 AUC(Area Under Curve)
AUC:AUC是ROC曲线下的面积,取值范围为0到1。AUC越大,模型的分类性能越好。
优点:对类别分布不敏感,适用于评估不同模型的整体性能。
缺点:无法直接反映精确率或召回率的具体数值。
3.10 对数损失(Log Loss)
对数损失:衡量模型预测概率分布与真实分布的差异。
L o g L o s s = − 1 N ∑ [ y i log ( y ^ i ) + ( 1 − y i ) log ( 1 − y ^ i ) ] Log \hspace{2pt} Loss=-\frac{1}{N}\sum{[y_i \log(\hat y_i)+(1-y_i)\log{(1-\hat y_i)}]} LogLoss=−N1∑[yilog(y^i)+(1−yi)log(1−y^i)]
优点:适用于概率输出模型,能反映模型的预测不确定性。
缺点:对分类错误非常敏感,数值范围较大,不易直观解释。
3.11 马修斯相关系数(Matthews Correlation Coefficient, MCC)
马修斯相关系数:考虑所有类别的分类性能,取值范围为-1到1,1表示完美的分类性能。
M C C = T P × T N − F P × F N ( T P + F P ) ( T P + F N ) ( T N + F P ) ( T N + F N ) MCC = \frac{TP \times TN-FP \times FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}} MCC=(TP+FP)(TP+FN)(TN+FP)(TN+FN)TP×TN−FP×FN
优点:适用于类别分布不均衡的场景。
缺点:计算较为复杂。
4 总结
4.1 回归指标总结
| 指标 | 适用场景 | 优点 | 缺点 |
|---|---|---|---|
| 均方误差 (MSE) | 数据中异常值较少 | 对异常值敏感,能够突出大误差的影响 | 单位是原始单位的平方,不直观 |
| 均方根误差 (RMSE) | 数据中异常值较少 | 单位与原始数据单位一致,更直观 | 对异常值敏感 |
| 平均绝对误差 (MAE) | 数据中有较多异常值 | 不对异常值敏感,更稳健 | 对于小误差和大误差的处理方式相同,可能无法突出大误差的影响 |
| 平均绝对百分比误差 (MAPE) | 需要百分比误差的情况 | 以百分比表示,便于比较不同规模的数据 | 当真实值接近零时,分母很小,可能引起数值不稳定或无穷大;不适用于分母为零的情况 |
| R² (R-squared) | 衡量模型解释的方差比例 | 取值范围从负无穷到1,1表示完美拟合;可以比较不同模型对数据的解释能力 | 可能会出现负值,表示模型比均值还要差;容易高估模型性能,尤其是特征较多时 |
| 调整R² (Adjusted R²) | 考虑模型复杂度 | 避免模型因增加特征而过度优化R² | 仍可能受到过拟合的影响 |
| 平均平方对数误差 (MSLE) | 目标值范围跨度大且为正数 | 适用于目标值范围跨度大的情况;减少大误差的影响 | 目标值需要为正数 |
| 均方根对数误差 (RMSLE) | 目标值范围跨度大且为正数 | 单位与对数变换后的单位一致,可能更直观 | 目标值需要为正数 |
| 最大误差 (Max Error) | 关注最坏情况的误差 | 直观反映模型可能犯下的最大错误 | 只关注最坏情况,可能不反映整体性能 |
| 中位数绝对误差 (MedAE) | 需要稳健性的情况 | 对异常值不敏感,因为使用中位数 | 不如均值敏感,可能无法反映整体误差 |
4.2 分类指标总结
| 指标 | 适用场景 | 优点 | 缺点 |
|---|---|---|---|
| Accuracy | 类别分布均衡 | 简单易懂 | 类别分布不均衡时可能误导 |
| Precision | 误报成本高(如垃圾邮件检测) | 关注预测的准确性 | 忽略漏报 |
| Recall | 漏报成本高(如疾病检测) | 关注模型的覆盖率 | 忽略误报 |
| F1-Score | 需要平衡精确率和召回率 | 综合考虑精确率和召回率 | 未考虑负类的影响 |
| ROC曲线 & AUC | 类别分布不均衡 | 直观展示模型性能 | 计算复杂 |
| Log Loss | 概率输出模型 | 能反映预测不确定性 | 数值范围大,不易直观解释 |
| 混淆矩阵 | 需要详细分析误差 | 全面展示分类结果 | 计算和解释复杂 |
| MCC | 类别分布不均衡 | 考虑所有类别的分类性能 | 计算复杂 |
参考学习

《评估机器学习的模型》,Alice Zheng,张建译, ISBN:9781491932469 ↩︎











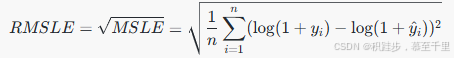



















 4471
4471

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










