正方形里面两个扇形相交部分_双正方形模型（一）

在正方形的题目中，有很常见的一类是和两个正方形有关的图形，如图1：

图1

在这个图形中，有很多有意思的性质，也衍生出了很多的题目．我们讲分几次一一道来．

「手拉手」模型

在学习全等的时候，我们知道有一类很重要的全等模型——旋转全等模型，俗称「手拉手」模型．说的是两个共顶点且顶角相等的等腰三角形，一定伴随着一组旋转全等，如图2：

图2

和

是两个顶角相等的等腰三角形，易证

．这是一个旋转全等，旋转角度等于两个等腰三角形的顶角角度．

关于这个模型，也有很多相关的结论，不过大部分和这次的内容关系不大，有机会我们另开文讲述．

那么，对于两个共顶点的正方形，也有类似的结论．在图1中，我们可以把它看成是两个等腰直角三角形

和

的「手拉手」，于是就有

，而且旋转角度为

．

图3

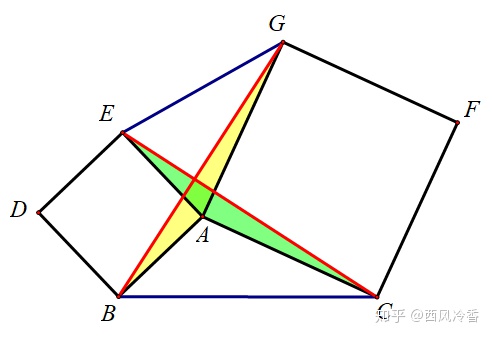
于是，我们就得到了一个对角线垂直且相等的四边形

．

和中点四边形相关的问题

熟悉中点四边形的朋友马上就会想到，这样一个四边形的中点四边形一定是一个正方形，也就是下面这个图：

图4

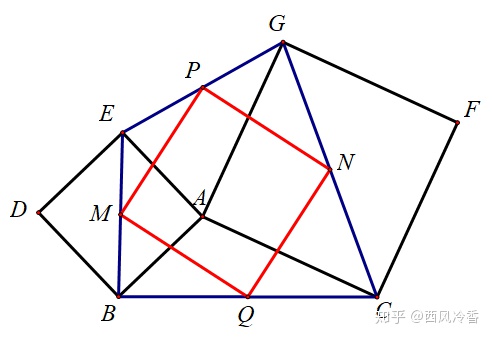
在这个图中，中点四边形

就是一个正方形．

另一个和中点相关的问题

在图1中，如果我们取

的中点

，连结

，则

且

．（如果取

中点，有类似的结论）

图5

对于中点问题，我们知道一种常见的处理方法就是「倍长中线」，因此我们倍长

至

，可以证明

．注意这是一个旋转

的全等，因此

和

垂直且相等，所以上面的结论成立．

图6

这个命题逆命题也成立，即如果

，则

为

的中点，且

．

这个命题也可以利用上图来证明，不过这个时候需要直接延长作

来证明全等．

这个时候另外一种处理方法是做垂直，利用弦图的模型来证明全等．

图7

如图7，延长

交

于

，作

于

，

于

，则

，

，于是

且

，因此

是平行四边形，于是

这两个证明同时还都证明了另一个结论，就是

．由割补法知这两个三角形的面积的确是相等的．

当然，如果熟悉三角函数的话，这两个三角形的面积相等是显然的．因为

和

互补，而角的两边对应相等，因此面积也是相等的．

变形一

前面我们说了

是一个对角线垂直且相等的四边形，因此，这个题的可以这样来出：

如图8，在四边形

中，

，且

，分别取

、

、

的中点

、

、

，分别过

、

作

、

的垂线交于

，则

．

图8

这个图如果把

、

、

、

都连起来，显然有

，注意这是一个旋转

的全等，因此

、

都是等腰直角三角形．于是这就变成了

图5一样的图了，后面的证明和上面相同．

图9

变形二

如果我们把两个正方形中间再加一个小正方形，那么结论会变成什么样子？

如图10，有三个正方形

、

、

，取

中点

，则有

且

．

图10

很明显，这个图是上面图5的一个推广，如果中间的小正方形缩成一个点，那么就变成了图5．

既然是推广，那么证明应该也是类似的．我们还是可以倍长

来做，不过这个时候要找的全等变得复杂了一些．

图11

如图11，我们倍长

至

，可以类似地证明

．

不过在证明的时候需要注意，这里面隐藏着两个「手拉手」的全等模型，在证明上面的全等的时候需要用到，如图12，有

，

，都是旋转

的全等．

图12

拓展联想

在圆的内接四边形中，有一个类似的结论：

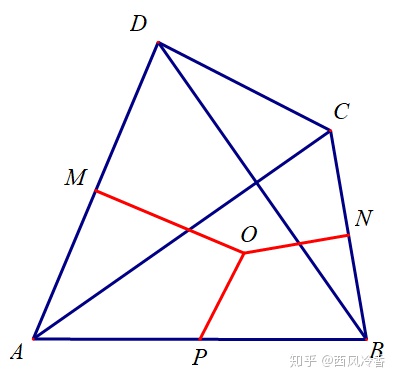
若圆内接四边形的对角线相互垂直，则垂直于一边且过对角线交点的直线将平分对边．

这就是 Brahmagupta 定理，一般译作「婆罗摩笈多定理」，或者「布拉美古塔定理」．

如图13，在圆的内接四边形

中，

，过对角线的中点

作

点

，交

于点

，则

是

的中点．

图13

这个的证明是比较简单的，

于是

故

，直接倒角就证明了．

这个定理的逆命题也成立，即如果

是

的中点，那么

．证明和上面类似．

---

总结一下，这类问题主要是和中点有关系，主要的方法是「倍长中线」和「手拉手」的全等．还有一类问题是借助于中位线来解决的，这一类题目讨论的不是

的中点（图2中），而是

的中点．这一类问题，我们放到下一篇文章中来讨论．