正方形里面两个扇形相交部分_【003】第二章 几个重要的拓扑概念-部分笔记

【更新一下 增加了概念地图和第四五小结】

最因为疫情在家宅，总算有点时间继续看数学了。

说实话目前看的部分与我自己的工作内容距离还是比较远的 ，不知道何年何月才能和手上实际的工作结合在一起。

不过就权当进行头脑体操，预防老年痴呆了。不过年纪大了，记忆力实在不如年轻的时候，公理多了就乱，内容要看好几遍才能记得下来，所以年轻人还是多学习吧，老了有点后悔当年没有好好学数学。

《基础拓扑学讲义》（尤承业 北京大学出版社）● 学习笔记

第二章 几个重要的拓扑概念 - 部分笔记

• 前言

• 这一章在说什么

在前一章节，通过定义开集，我们构建了一种更为广泛意义上的空间结构：拓扑空间。但是构建这个空间结构的初衷之一是将欧氏空间的一些概念延展过来，而前面定义的拓扑空间过于一般性。

为此本章节定义了更多相对高级的概念，来约束空间结构。

本章节主要是介绍：可分离性、可数性、紧致性和联通性

这一章可以明显看到前人从无到有去逐渐构造各种数学空间的过程。脑子里面来源于欧氏空间的概念，在这些空间中并非天经地义，而是由一些列更为基础的性质逐渐构造来的，非常有意思。

最终我们在工科中使用的往往都是性能非常好的空间结构，一般并不会讨论这些结构性质的来源，不过了解一下本章节涉及到的定义、名称、概念还是非常有意义的。

这一章节都是各种抽象的概念，死背定记不住， 学习的时候一定要想办法对每个概念有“直观”的理解
相关的“直观”理解可以在网上找一下，这个很重要

下面是这一张的概念地图：

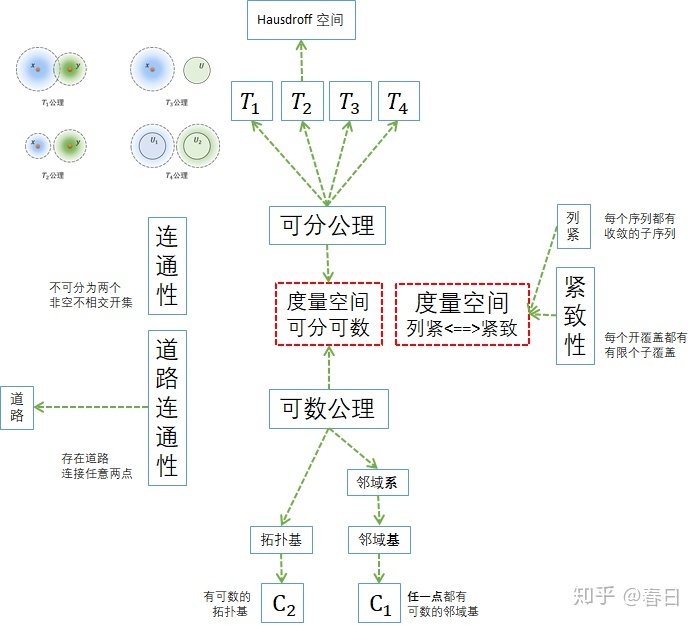
只是为了方便记忆

• 第一节：分离公理和可数公理

要注意之前给出的拓扑定理只是给出了拓扑空间的最最基本的性质，而不是拓扑空间的全部性质！这种缺失会让后续的推到和证明缺少根基，为此需要补充一些空间结构的性质。其中分离性和可数性常作为附加性质来弥补拓扑公理的不足。

有两个可数公理和四个分离公理

。

• 分离公理

分离公理都是关于两个点（或者是闭集）能否通过邻域来分割的性质。

公理：任何两个不同点

与

，

有邻域不包含

,同时

有邻域不包含

。

公理：任何两个不同点有不相交的邻域。

公理：任何一点与不包含它的任一闭集有不相交的邻域。

公理：任何两个不相交的闭集有不相交的邻域。

这里的"邻域"改为开邻域也是完全正确的。（邻域就是包含点的开集）

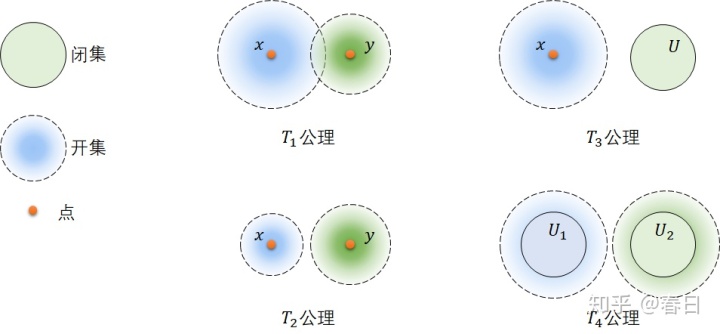
这里绘制了这个几个概念的示意图，虽然用欧氏空间的图来讲解概念不是个好习惯，但是对于工科的我更容易记忆，大家多包含吧。

• 分离公理 的一些推论

可数公理分为：第一可数公理

和第二可数公理

，满足

的拓扑空间被称为：

空间，

空间又被称为完全可数空间。

1. 满足
   公理 等价于
   的有限子集是闭集
2. 满足
   公理 等价于 任意点
   和它的开邻域
   ，存在
   的开邻域
   ，使得
3. 满足
   公理 等价于 任意闭集
   和它的开邻域
   ，存在
   的开邻域
   ，使得
4. 空间：
   公理是最重要的分离公理 ，满足
   公理的空间被称为
   空间。
5. *空间中一个序列不会收敛到两个点
6. 度量空间
   满足所有分离公理

• 可数公理

可数公理分为： 第一可数公理

和第二可数公理

，满足

的拓扑空间被称为：

空间，

空间又被称为完全可数空间。

首先定义几个基础概念：

邻域系：设

.把

所有邻域的集合称为

的邻域系，记作

邻域基：

的一个子集

被称为邻域基，如果

的每个邻域至少包含

中

的一个成员。（

是可以完整描述

邻域这个一概念的更小的集合）

（

是可以完整描述

邻域这个一概念的更小的集合）

可数集：每个元素都能与自然数集N的每个元素之间建立一一对应的集合

公理：任一点都有可数的邻域基。

公理：有可数的拓扑基。

•

公理 的解释和性质

1. 度量空间满足
   公理 ： 说明：可以构造球形邻域系，
   ，它显然满足邻域基的要求，同时它与自然数集合元素一一对应，因此是可数的。
2. 如果
   在
   处有可数的邻域基，则
   有可数的邻域基
   ，使得
3. 诺
   是
   空间，
   ，且
   ，则
   中存在收敛到
   的序列。

•

公理 的解释和性质

1. 公理是一个很强的要求，以至于一些度量空间也不是
   空间
2. 一定也是
   空间
3. 空间是可分空间
4. 可分度量空间是
   空间
5. Hilbert空间是
   空间

• 拓扑性质的遗传性和可乘性

1. 遗传性：拓扑空间具有的性质，子空间也具有
2. 可乘性：两个空间都具有的性质，乘积空间也具有

• 补充一些相关概念：

柯西序列: 在数学中，一个柯西序列是指一个这样一个序列，它的元素随着序数的增加而愈发靠近。更确切地说，在去掉有限个元素后，可以使得余下的元素中任何两点间的距离的最大值不超过任意给定的正的常数。柯西列是以数学家奥古斯丁·路易·柯西的名字命名的。

完备空间：完备空间或者完备度量空间是具有下述性质的空间：空间中的任何柯西序列都收敛在该空间之内。以有限维空间来说，向量的范数相当于向量的模的长度。

线性空间：向量空间又称线性空间，是线性代数的中心内容和基本概念。

赋范线性空间：赋范线性空间(normed linear space)是在线性空间中引进一种与代数运算相联系的度量，即由向量范数诱导出的度量。赋范线性空间称为Banach空间，是指由范数导出的度量是完备的。

内积空间：在数学里面，内积空间是增添了一个额外的结构的向量空间。这个额外的结构叫做内积，或标量积，或点积。这个增添的结构允许我们谈论向量的角度和长度。内积空间由欧几里得空间抽象而来，这是泛函分析讨论的课题。

Hilbert空间：完备的内积空间被称为希尔伯特空间（Hilbert）。希尔伯特空间是欧几里德空间的直接推广，希尔伯特空间也是一个内积空间，其上有距离和角的概念。希尔伯特空间还是一个完备的空间，其上所有的柯西序列等价于收敛序列，从而微积分中的大部分概念都可以无障碍地推广到希尔伯特空间中。

• 第二节：

引理 和

扩张定理

两个定理都是

公理的等价条件。

•

引理（urysohn引理）

Urysohn: 中文翻译是：乌雷松，

实在是不知道如何读音，大家知道的可以回复我一下，感谢

定义：如果拓扑空间

满足

公理。则对于

上的任意两个不相交闭集

和

，存在

上的连续函数

，它在

和

上的取值分别是0和1.

应用：

引理和

公理是等价的。

•

扩张定理

定义：如果

满足

公理，则定义在

的闭子集

上的连续函数可连续的扩张到

上。

太有用了，证明函数在闭子集上连续，就可被推广到整个集合。

应用：Tietze定理和

公理是等价的。

下面开始讨论度量化的问题也是本节的重点

•

度量化定理

（urysohn度量化定理）

可度量化：一个拓扑空间

是可度量的，如果可以在集合

上规定一个度量

，使得

.

命题：拓扑空间

是可度量的

到一个度量空间的嵌入映射

Urysohn度量化定理：拓扑空间

满足

和

公理

可以嵌入到到Hilbert空间

中

是可度量的。

是

维的欧式空间

Urysohn度量化定理的作用是给出了如何证明一个空间是可度量的！

• 第三节：紧致性

首先说一下序列相关的概念：

列紧：拓扑空间是列紧的，如果他的每个序列都有收敛的子序列。

命题：定义在列紧拓扑

空间上的连续函数

，是有界的，可以取得最大值和最小值。

在拓扑空间中，序列不是一种好的表达形式，因此 紧致性概念使用开集表达形式来描述上述性质。

紧致性：拓扑空间称为紧致的，如果它的每个开覆盖都有有限个子覆盖。

紧致性：是一种最基本、最常见的拓扑性质
紧致性与列紧看起来没有直接联系，但是他们之间却有着密切的关系，尤其是度量度量空间上，这两种性质是等价的！（其他空间不一定）

紧致度量空间

命题：紧致

空间是列紧的

由于度量空间满足

空间，因此紧致的度量空间是列紧的。

-网：

度量空间

的子集

称为

的

-网，

有

这个定义可以等价于：

命题：对于任意

，列紧度度量空间存在有限的

-网（

是一个正数）

省略了Lebesgus数的部分，感兴趣大家自行阅读

命题：列紧度量空间是紧致的。

定理：如果

是度量空间：则

是列紧的<==>

紧致

这个定理由上述命题得到

• 紧致空间的性质

证明了一大堆，紧致空间到底有什么好处？

紧致子集：一个拓扑空间

的子集

如果作为子空间是紧致的，就称为

的紧致子集

命题：

是

的紧致子集 <===>

在

中的任一开覆盖有有限的子覆盖

命题：紧致空间的闭子集紧致

命题：紧致空间在连续函数映射下的像也紧致

• Hausdorff空间（

空间）的紧致子集

公理和紧致性共同作用的性质

命题：若

是Hausdorff空间

的紧致子集，

，则

与

有不相交的邻域。

推论：Hausdorff空间的紧致子集是闭集

定理：设

是连续的一一对应，其中

是紧致的，

是Hausdorff空间，则

是同胚的。

命题：Hausdorff空间的不相交紧致子集有不相交的邻域

• 乘积空间紧致性

紧致的可乘性：若

和

都是紧致的，则

也是紧致的

这个性质可以推广到无穷多个空间构成的乘积空间

• 局部紧致性与仿紧

紧致性是一种很好的拓扑性质，但是它太强了，连欧氏空间也不是紧致的!
为此提出了两种紧致性额的推广：局部紧致和仿紧

局部紧致：拓扑空间

称为局部紧致，如果对于

有紧致的邻域。

欧氏空间 是局部紧致的。

加细：设

和

都是X的覆盖，如果

中每个成员都包含在

的某称成员中，则称

是

的加细，如果

是开覆盖，则称

是

的开加细。

仿紧：拓扑空间

被称为仿紧的，如果X的每个开覆盖都有U局部有限的开加细

了解了解概念就好 不强求~ ~ ~ ~

• 第四节 连通性

• “连通”的两个直观含义“：

​ 1、图形不能分割为两个互不”粘连“的部分 【拓扑学中对应为：连通性】

​ 2、图形上任意两个点可以以讴歌图形上的线链接 【拓扑学中对应为：道路连通性】

• 连通性的定义

连通性定义:拓扑空间

是连通的，如果它不能分解为两个非空不相交开集合的并

• 连通性的性质

命题：连通空间在连续映射下也是连通的

命题：若

有一个连通的稠密子集，则

连续

稠密的直观解释参考
稠密跟连续有一步之差，连续是说数轴上你随便选个地方一刀切下去，切点上一定有一个实数，这个就叫实数的连续性。对有理数这个就不成立了，一刀下去有可能刚好切空了没切到有理数；但是如果你用两刀削下来一个有长度的线段（开区间），不管你刀工多精妙，线段长度再小，只要不为0，其中就一定有至少一个——甚至可以说，有无穷多个有理数。这个就叫做有理数的稠密性。把线段（开区间）换成空心邻域，最多少一个有理数，那么剩下的有理数仍然是无限多个，也就是说任意一个点的任意空心邻域中都仍然有有理数。
作者：灵剑 链接： https://www. zhihu.com/question/3557 0204/answer/130377390 来源：知乎

命题：

如果

有一个连通覆盖

(

的每个成员都是连通的)，并且

有一个连通子集

，与

中每个成员都相交，则

是连通的

很直观啊，画两个心，再画一个箭穿过它们，哈哈哈~~~

• 连通分支

定义：拓扑空间

的一个子集成为

的连通分支，如果： 1）它是连通的

​ 2）它不是

的其他连通子集的真子集

真子集：如果A包含于B,且A不等于B,就说集合A是集合B的真子集

命题：

的每个非空连通子集都包含在唯一的一个连通分支中

命题：连通分支是闭集

• 局域连通性

定义：拓扑空间

称为局部连通的，如果

，

的所有连通邻域构成

的邻域基

每个邻域中都有连通邻域

注意：连通空间不一定是局域连通的

命题：局域连通空间的连通分支是开集

• 第五节 道路连通性

• 道路

直观理解：“道路”是“曲线”这种直观概念的抽象化

定义：设

是拓扑空间，从单位闭区间

到

的一个连续映射

称为

上的一条道路。

起点：

终点：

道路有两种运算：逆 和 乘积

道路的逆：一条道路

的逆也是

上的道路，记作

，规定：

道路的乘积：

上的两条道路，

和

如果满足：

，则规定他们两个的乘积为：

，它也是

上的道路，规定为：

• 道路连通空间

定义：拓扑空间

称为道路连通的，如果

存在

中分别以

和

为起点和终点的道路

命题：道路连通空间一定连通

命题：道路连通空间的连续映像是道路连通的

• 道路连通分支

• 局部道路连通

感兴趣的请自行阅读