强化学习的本质贝尔曼最优方程理解

强化学习的各种方法都是围绕贝尔曼公式和贝尔曼最优公式进行的，强化学习牵涉的概念较多，不易理解，公式中包含的符号较多，容易绕晕，本文从一些基本的概念出发，阐述状态、策略、动作、奖励的原始概念，然后导出贝尔曼公式，并给出相关的例子，便于理解概念。

1 计算return的方法

一个智能体，在环境中，会采用不同的动作，得到不同的奖励
从起点出发，转移到其它状态，并根据一定的折扣因子（我更喜欢物理学中的衰减因子这个称呼）进行奖励衰减，折扣因子的引入是为了权衡当前奖励和未来奖励的权重，当折扣因子为0时就相当于只重视当前短期的利益，而折扣因子为1时，就看中长远利益。

上面不同的状态v的未知数，转换为矩阵形式就可以求解方程，而这个表达式就是特殊的确定性策略下的贝尔曼公式

2 state_value

有了上面的概念，下面给出一般意义下的状态值的定义。

求不同策略π下得到的Gt均值

举例说明，以下通过三种策略，s1到终点s4，求取s1的state_value为：

在上面求解过程中，策略给定后就是确定性的问题了，到达终点后一直在终点保持不动，就会形成无限多的变量。

贝尔曼公式

求取状态在所有策略下奖励的均值。
包含两部分，立即奖励和未来奖励，是不同状态和策略之间的相互关系，状态值越大，说明该状态越有意义。

举例说明：

写成矩阵向量形式：

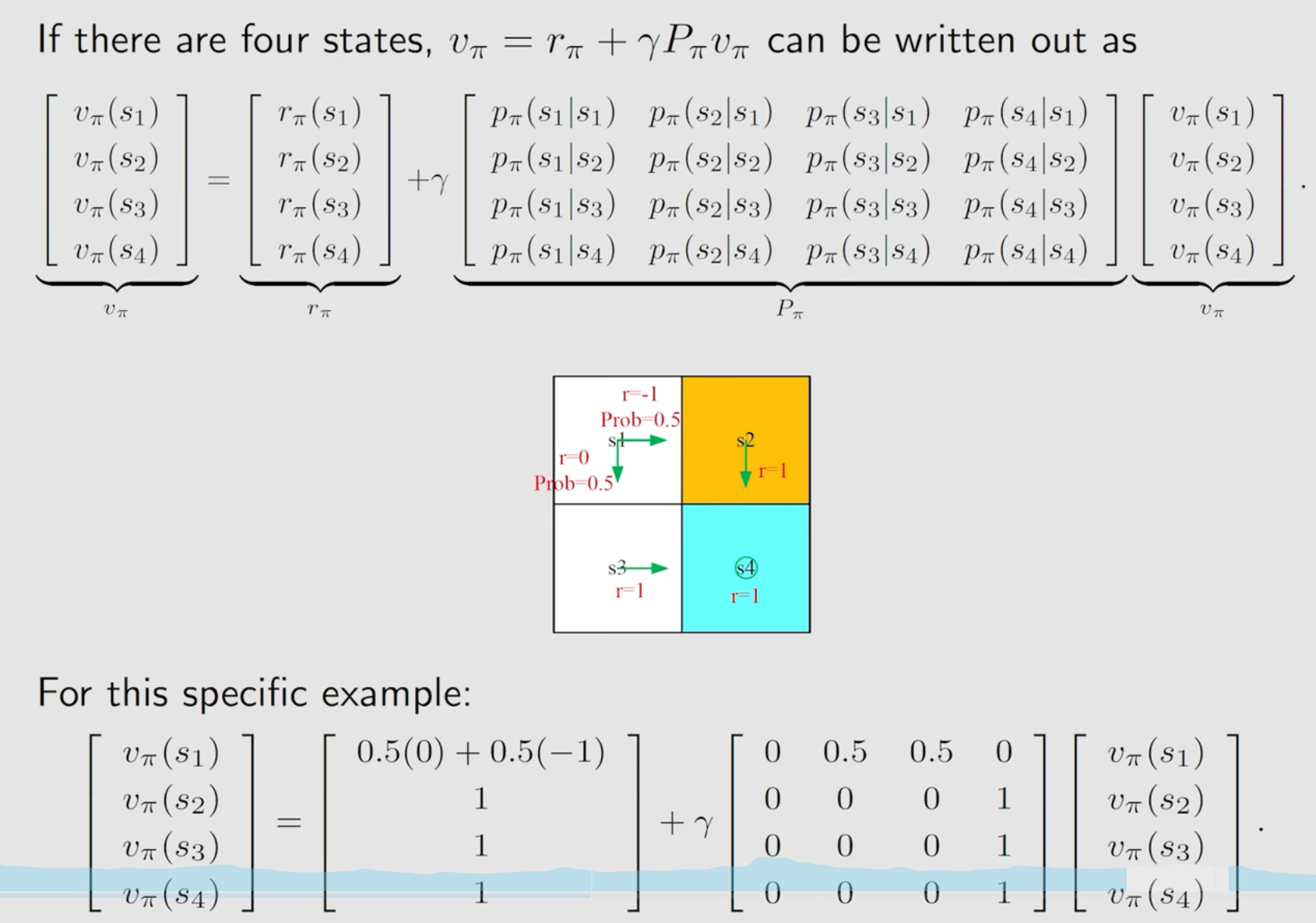
求解贝尔曼方程有两种方法：

一种是解析法（需要知道状态转移概率P，但现实中很难知道）；

一种是迭代法（可以证明在折扣因子在0到1之间时是收敛的）；

策略评估policy evaluation：

给定策略π，计算所有的状态值。

状态值和动作值：

状态值：从一个状态返回的回报的均值

动作值：从一个状态和一个动作返回的回报的均值

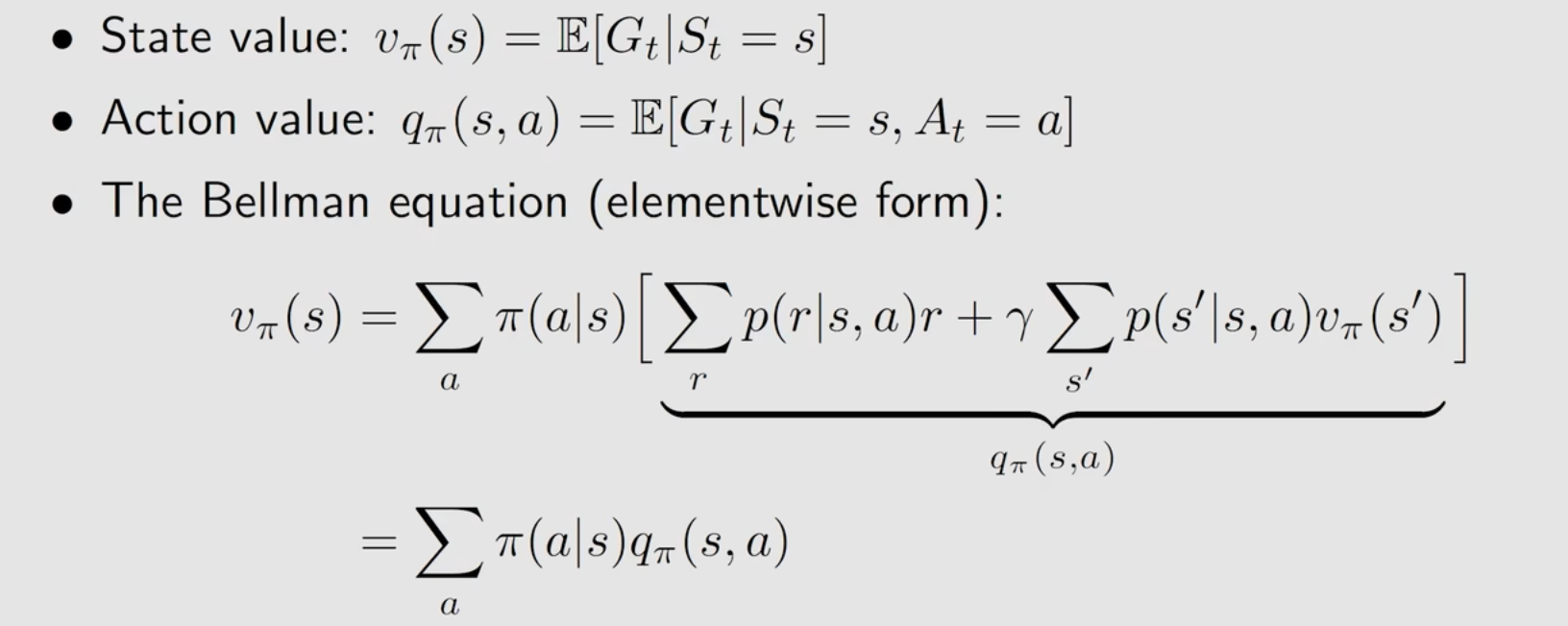
贝尔曼最优公式

需要求解最优策略π，使得v最大。

已知状态转移概率p，r和γ，求π和v。

不动点理论：

贝尔曼最优公式的解的性质

• 存在性
• 唯一性
• 指数收敛
• 可迭代性