MATLAB PDE工具箱电磁场仿真平行电容板及电偶极子详解

首先打开matlab，在命令行输入pdetool打开PDE工具箱

工具箱的功能我就不赘述了，大概就是以有限元的数值计算方法，计算二阶偏微分方程，因此可以解决电磁场、热力学等问题。

首先点击左上角按钮，画三个矩形

画完一个后可以双击矩形编辑，参数如下：



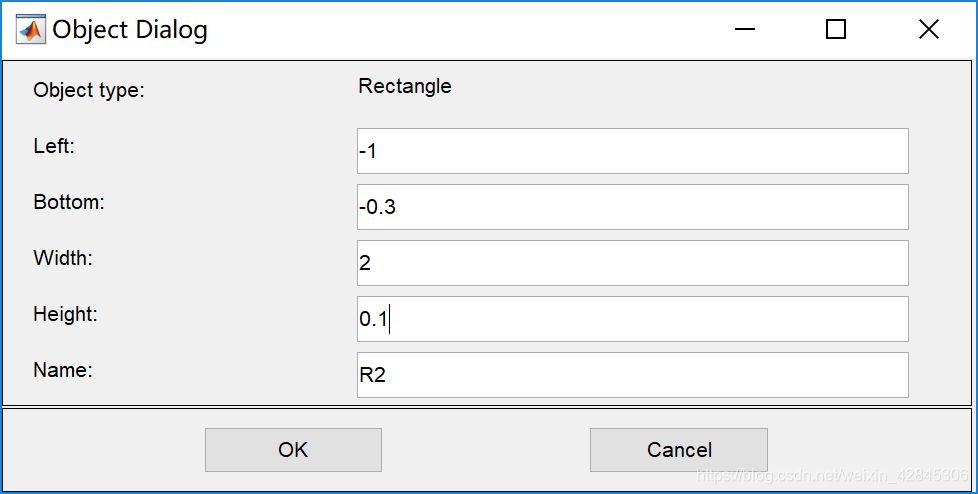
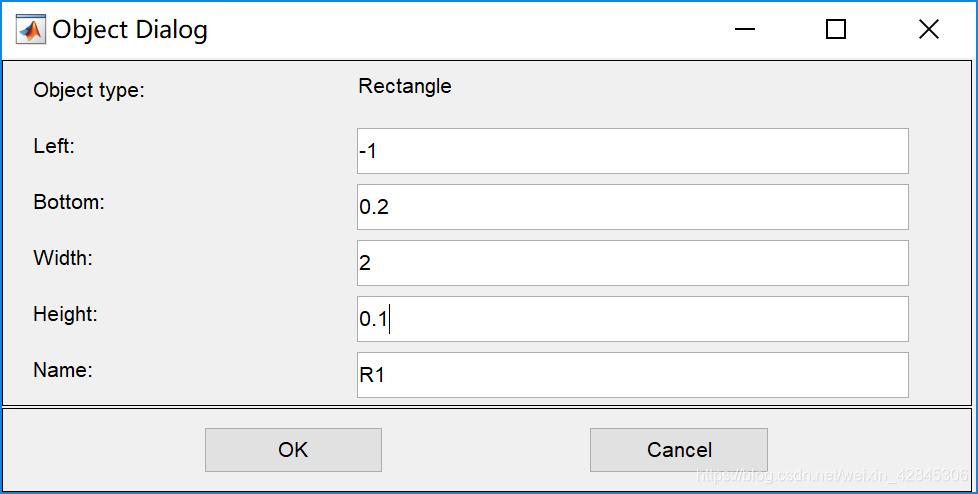
其中R1表示上极板，R2表示下极板，R3表示整个空间区域。

在上方Set formula为R3-R2-R1，表示求解区域是整个空间区域减去两个极板。下拉框选择Electrostatics表示求解的是静电场问题。
接下来点击上方菜单栏中的这个按钮，表示编辑边界条件。


红色线表狄利克雷边界，按住shift连续点击上极板的四个边界（选中会变黑）最后双击，可以打开边界编辑框。

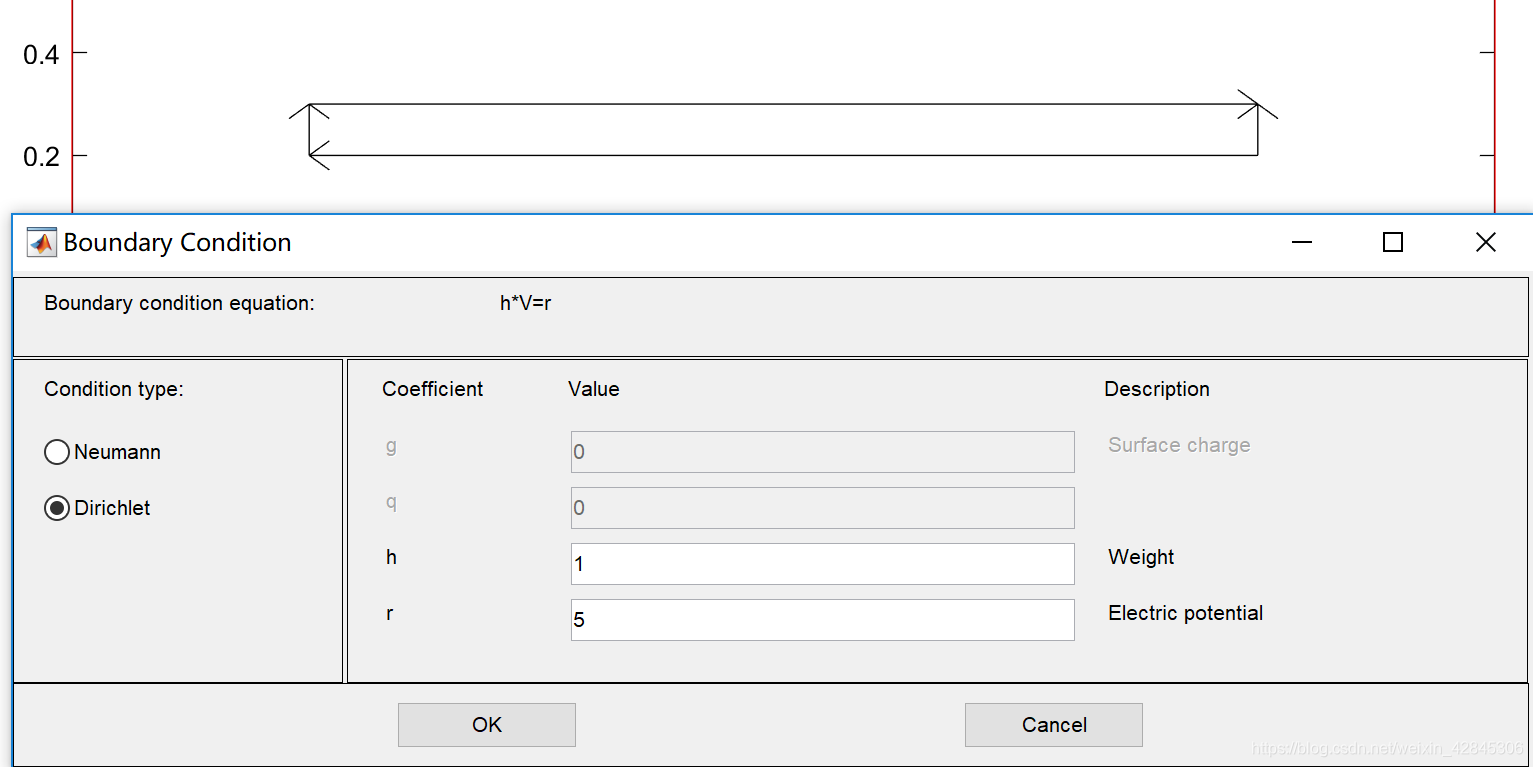
选择狄利克雷边界（第一类边界条件，给定边界的值）
上面是纽曼边界（第二类边界条件，给定边界的导数值）
此外还有混合边界（混合第一第二类的情况）
权重h设置为1，上极板电位设置为5v。

重复上述步骤，将R2的四个边界电位设置为-5v，R3的四个边界电位设置为0v（表示无穷远处电位为0）

点击上方菜单栏中的PDE按钮，可以看到计算公式，默认是泊松方程，就是电磁场里面很熟悉的：
$$\nabla \cdot E=\frac{\rho }{ϵ}$$
$$E=\nabla v$$

不过我们研究的区域没有电荷源（或者认为两个电容板带电大小相等极性相反，抵消了），于是设置rho=0，等式变为了拉普拉斯方程，即
$${\nabla }^{2}v=0$$

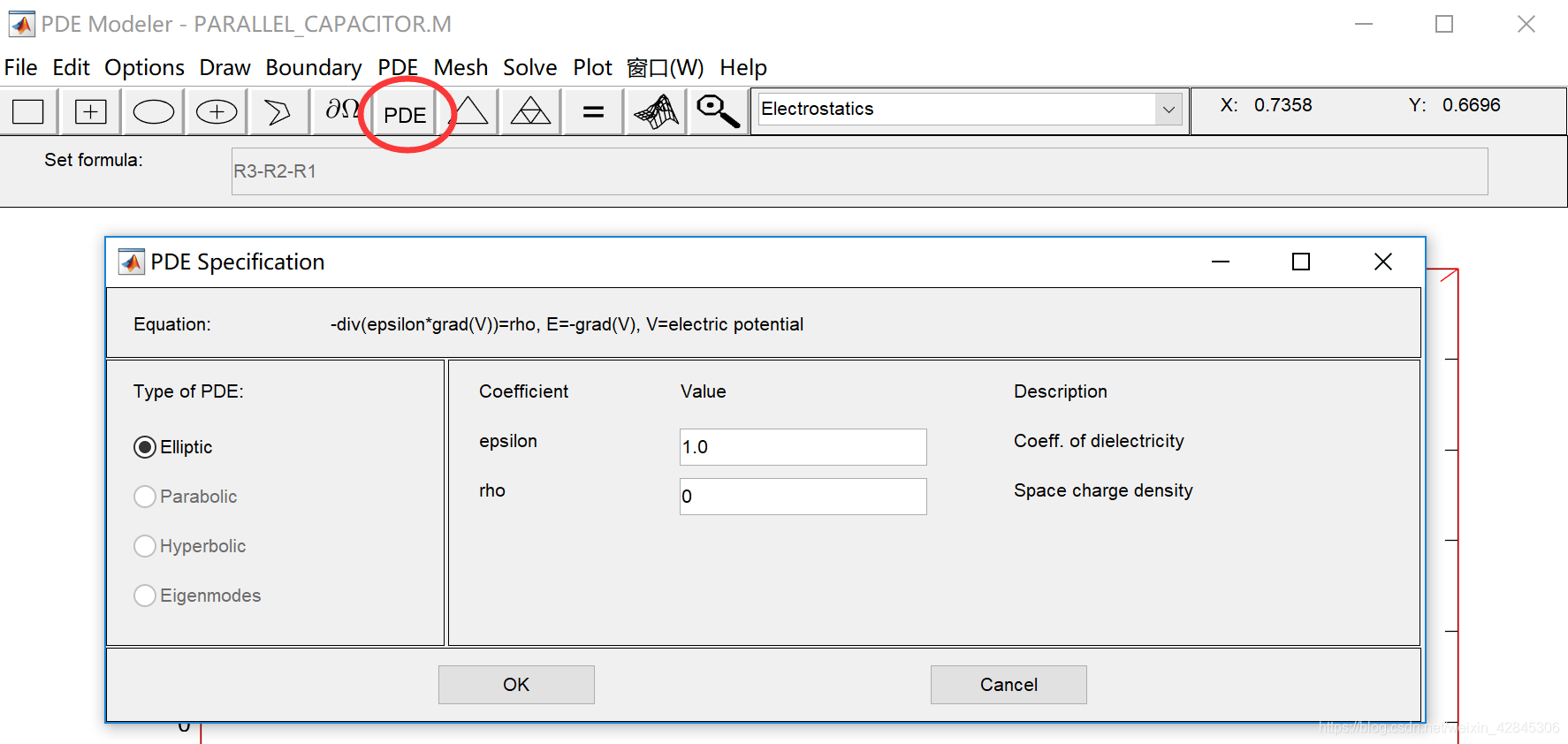
随后点一下上方菜单里的三角（下图红圈内的），可以将求解区域用有限元划分，然后点击若干次加密三角（下图蓝圈内的），可以把求解区域进一步细分，分的越细，精度越高、速度越慢。

最后点击右边那个等号，进行求解，得出电场分布图如下：

红色箭头是电场强度矢量，黑色一圈圈的线是等势线，颜色代表电位高低。可以看到在两个极板中间，可以近似认为是均匀电场，等势线平行分布。
菜单栏里面长得像matlab图标的那个按钮，是绘图参数

左侧可以显示颜色、等势线、场强箭头等设置。
在Mesh和Solve中可以将结果导出，分别是网格划分结果和对应的计算电位值（但是我不知道怎么用），在File里面可以把当前画的图导出，不过不能导出成fig

电偶极子仿真跟上述类似。两个相距很近的带等量异号电荷的点电荷为电偶极子。首先先画出这两个（近似）点电荷E1和E2，圆半径为0.05，y位置均为0，x位置分别为-0.1和+0.1。最后别忘了构造整个空间区域R1，并设置求解区域为R1-E1-E2
示例E1的参数如图：

边界条件设置E1电位5v，E2电位-5v，边界为0v。
细分网格，如下图所示

有那么一点吓人……
其余设置同上，记得要调整为拉普拉斯方程，求解结果如下图

如上图所示，电偶极子的等势面在两个电荷之间非常密集，而在这之外变得比较稀疏、且对称。可以发现在远场处，左右等势面合并可以近似为一个圆，这暗示我们可以将电偶极子当做一个特殊的电荷处理。