计算机视觉基础特征选择和特征提取

最新推荐文章于 2023-06-22 15:14:00 发布

pengege666

最新推荐文章于 2023-06-22 15:14:00 发布

阅读量1.3k

点赞数 1

分类专栏：计算机视觉理论文章标签：算法机器学习 python

本文链接：https://blog.csdn.net/weixin_42888638/article/details/121719301

版权

计算机视觉理论专栏收录该内容

12 篇文章 0 订阅

订阅专栏

1.特征选择

前置知识

一个对象往往具有很多属性（以下称为特征）(例如：房价的特征可能有地段，面积等一系列属性所影响)
•相关特征：对于学习任务（例如分类问题）有帮助，可以提升学习算法的效果；
•无关特征：对于我们的算法没有任何帮助，不会给算法的效果带来任何提升；
•冗余特征：不会对我们的算法带来新的信息，或者这种特征的信息可以由其他的特征推断出。

目的

特征选择的主要目的：
• 降维
• 降低学习任务的难度
• 提升模型的效率

定义

从N个特征中选择其中M（M<=N）个子特征，并且在M个子特征中，准则函数可以达到最优解。
OR
选择尽可能少的子特征，模型的效果不会显著下降，并且结果的类别分布尽可能的接近真实的类别分布。

操作过程

特征选择主要包括四个过程：
1.生成过程：生成候选的特征子集；
2.评价函数：评价特征子集的好坏；
3.停止条件：决定什么时候该停止；
4.验证过程：特征子集是否有效；

生成过程

生成过程是一个搜索过程，
这个过程主要有以下三个策略：
1.完全搜索：根据评价函数做完全搜索。完全搜索主要有两种：穷举搜索和非穷举搜索;
2.启发式搜索：根据一些启发式规则在每次迭代时，决定剩下的特征是应该被选择还是被拒绝。这种方法很简单并且速度很快。
3.随机搜索：每次迭代时会设置一些参数，参数的选择会影响特征选择的效果。由于会设置一些参数（例如最大迭代次数）

评价函数

评价函数主要用来评价选出的特征子集的好坏，一个特征子集是最优的往往指相对于特定的评价函数来说的。评价函数主要用来度量一个特征（或者特征子集）可以区分不同类别的能力。
根据具体的评价方法主要有三类：
•过滤式（filter)[就是先筛部分，再进行训练]:先进行特征选择，然后去训练学习器，所以特征选择的过程与学习器无关。相当于先对于特征进行过滤操作，然后用特征子集来训练分类器。对每一维的特征“打分”，即给每一维的特征赋予权重，这样的权重就代表着该维特征的重要性，然后依据权重排序。
•包裹式（wrapper）[由分类器给子集进行评优，选择子集]：直接把最后要使用的分类器作为特征选择的评价函数，对于特定的分类器选择最优的特征子集。将子集的选择看作是一个搜索寻优问题，生成不同的组合，对组合进行评价，再与其他的组合进行比较。这样就将子集的选择看作是一个优化问题，
•Filter和Wrapper组合式算法：先使用Filter进行特征选择，去掉不相关的特征，降低特征维度；然后利用Wrapper进行特征选择。
•嵌入式（embedding）[由模型完成特征的挑选]：把特征选择的过程与分类器学习的过程融合一起，在学习的过程中进行特征选择。其主要思想是：在模型既定的情况下学习出对提高模型准确性最好的属性。这句话并不是很好理解，其实是讲在确定模型的过程中，挑选出那些对模型的训练有重要意义的属性。
一般有5种比较常见的评价函数：
1.距离度量：如果X 在不同类别中能产生比Y 大的差异，那么就说明X 要好于Y;
2.信息度量：主要是计算一个特征的信息增益（度量先验不确定性和期望, 后验不确定性之间的差异）；
3.依赖度量：主要用来度量从一个变量的值预测另一个变量值的能力。最常见的是相关系数：用来发现一个特征和一个类别的相关性。如果X 和类别的相关性高于Y与类别的相关性，那么X优于Y。对相关系数做一点改变，用来计算两个特征之间的依赖性，值代表着两个特征之间的冗余度。
4.一致性度量：对于两个样本，如果它们的类别不同，但是特征值是相同的，那么它们是不一致的。否则是一致的。找到与全集具有同样区分能力的最小子集。严重依赖于特定的训练集和最小特征偏见（Min-Feature bias）的用法；找到满足可接受的不一致率（用户指定的参数）的最小规模的特征子集。
5.误分类率度量：主要用于Wrapper式的评价方法中。使用特定的分类器，利用选择的特征子集来预测测试集的类别，用分类器的准确率来作为指标。这种方法准确率很高，但是计算开销较大。

停止条件

停止条件用来决定迭代过程什么时候停止，生成过程和评价函数可能会对于怎么选择停止条件产生影响。停止条件有以下四种选择：
1.达到预定义的最大迭代次数；
2.达到预定义的最大特征数；
3.增加（删除）任何特征不会产生更好的特征子集；
4.根据评价函数，产生最优特征子集；

2.特征提取

定义

特征提取：是通过属性间的关系，如组合不同的属性得到新的属性，这样就改变了原来的特征空间。

与特征选择的区别

与特征选择的区别：特征提取与特征选择都属于降维，不过二者有着本质上的区别；特征选择能够保持数据的原始特征，最终得到的降维数据其实是原数据集的一个子集；而特征提取会通过数据转换或数据映射得到一个新的特征空间，尽管新的特征空间是在原特征基础上得来的，但是凭借人眼观察可能看不出新数据集与原始数据集之间的关联。

目的

主要目的是为了排除信息量小的特征，减少计算量等。

方法

目前图像特征的提取主要有两种方法：传统图像特征提取方法和深度学习方法
1.传统的特征提取方法：基于图像本身的特征进行提取；
2.深度学习方法：基于样本自动训练出区分图像的特征分类器；

3.PCA（主成分分析）

介绍

简单来说，就是将数据从原始的空间中转换到新的特征空间中，例如原始的空间是三维的(x,y,z)，x、y、z分别是原始空间的三个基，我们可以通过某种方法，用新的坐标系(a,b,c)来表示原始的数据，那么a、b、c就是新的基，它们组成新的特征空间。在新的特征空间中，可能所有的数据在c上的投影都接近于0，即可以忽略，那么我们就可以直接用(a,b)来表示数据，这样数据就从三维的(x,y,z)降到了二维的(a,b)。

步骤

一般步骤是这样的：
1.对原始数据零均值化（中心化）
2.求协方差矩阵
3.对协方差矩阵求特征向量和特征值，这些特征向量组成了新的特征空间

具体原理

中心化

中心化即是指变量减去它的均值，使均值为0。
其实就是一个平移的过程，平移后使得所有数据的中心是(0,0)
因为只有中心化数据之后，计算得到的方向才能比较好的“概括”原来的数据。
在这里插入图片描述

PCA降维

我们对于一组数据，如果它在某一坐标轴上的方差越大，说明坐标点越分散，该属性能够比较好的反映源数据（因为差异越大，越容易分类）。所以在进行降维的时候，主要目的是找到一个超平面，它能使得数据点的分布方差呈最大，这样数据表现在新的坐标轴上时候已经足够分散了。

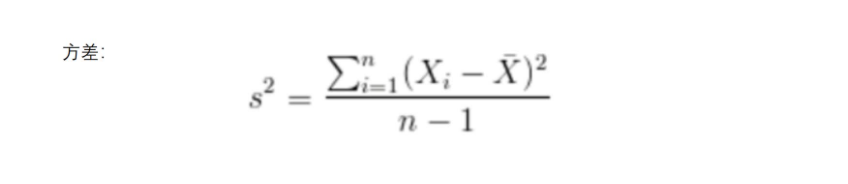
在这里插入图片描述
PCA算法的优化目标就是:
①降维后同一维度的方差最大
②不同维度之间的相关性为0

协方差矩阵

协方差就是一种用来度量两个随机变量关系的统计量。
同一元素的协方差就表示该元素的方差，不同元素之间的协方差就表示它们的相关性。（S^2:表示方差的平方）
在这里插入图片描述

D(X):表示同一元素的方差.

在这里插入图片描述

正相关是指自变量增长，因变量也跟着增长。同理，负相关。

求解特征值和特征向量的原理

解释：将排好序的特征值所对应的特征向量依次组成(nk)的矩阵(设为：矩阵M），将原先的矩阵X和M矩阵相乘，即（nn）(nk)==>(n*k)
在这里插入图片描述

优缺点

在这里插入图片描述

代码实现部分

方式一：

import numpy as np


class PCA():
    def __init__(self, n_components):
        self.n_components = n_components

    def fit_transform(self, X):
        self.n_features_ = X.shape[1]
        # 求协方差矩阵
        X = X - X.mean(axis=0)
        self.covariance = np.dot(X.T, X) / X.shape[0]
        # 求协方差矩阵的特征值和特征向量
        eig_vals, eig_vectors = np.linalg.eig(self.covariance)
        # 获得降序排列特征值的序号
        idx = np.argsort(-eig_vals)
        # 降维矩阵
        self.components_ = eig_vectors[:, idx[:self.n_components]]
        # 对X进行降维
        return np.dot(X, self.components_)

# 调用
pca = PCA(n_components=2)
X = np.array(
    [[-1, 2, 66, -1], [-2, 6, 58, -1], [-3, 8, 45, -2], [1, 9, 36, 1], [2, 10, 62, 1], [3, 5, 83, 2]])  # 导入数据，维度为4
newX = pca.fit_transform(X)
print(newX)  # 输出降维后的数据

方式二：

"""
使用PCA求样本矩阵X的K阶降维矩阵Z
"""
  
import numpy as np
  
class CPCA(object):
    '''用PCA求样本矩阵X的K阶降维矩阵Z
    Note:请保证输入的样本矩阵X shape=(m, n)，m行样例，n个特征
    '''
    def __init__(self, X, K):
        '''
        :param X,训练样本矩阵X
        :param K,X的降维矩阵的阶数，即X要特征降维成k阶
        '''
        self.X = X       #样本矩阵X
        self.K = K       #K阶降维矩阵的K值
        self.centrX = [] #矩阵X的中心化
        self.C = []      #样本集的协方差矩阵C
        self.U = []      #样本矩阵X的降维转换矩阵
        self.Z = []      #样本矩阵X的降维矩阵Z
         
        self.centrX = self._centralized()
        self.C = self._cov()
        self.U = self._U()
        self.Z = self._Z() #Z=XU求得
         
    def _centralized(self):
        '''矩阵X的中心化'''
        print('样本矩阵X:\n', self.X)
        centrX = []
        mean = np.array([np.mean(attr) for attr in self.X.T]) #样本集的特征均值
        print('样本集的特征均值:\n',mean)
        centrX = self.X - mean ##样本集的中心化
        print('样本矩阵X的中心化centrX:\n', centrX)
        return centrX
         
    def _cov(self):
        '''求样本矩阵X的协方差矩阵C'''
        #样本集的样例总数
        ns = np.shape(self.centrX)[0]
        #样本矩阵的协方差矩阵C
        C = np.dot(self.centrX.T, self.centrX)/(ns - 1)
        print('样本矩阵X的协方差矩阵C:\n', C)
        return C
         
    def _U(self):
        '''求X的降维转换矩阵U, shape=(n,k), n是X的特征维度总数，k是降维矩阵的特征维度'''
        #先求X的协方差矩阵C的特征值和特征向量
        a,b = np.linalg.eig(self.C) #特征值赋值给a，对应特征向量赋值给b。函数doc：https://docs.scipy.org/doc/numpy-1.10.0/reference/generated/numpy.linalg.eig.html 
        print('样本集的协方差矩阵C的特征值:\n', a)
        print('样本集的协方差矩阵C的特征向量:\n', b)
        #给出特征值降序的topK的索引序列
        ind = np.argsort(-1*a)
        #构建K阶降维的降维转换矩阵U
        UT = [b[:,ind[i]] for i in range(self.K)]
        U = np.transpose(UT)
        print('%d阶降维转换矩阵U:\n'%self.K, U)
        return U
         
    def _Z(self):
        '''按照Z=XU求降维矩阵Z, shape=(m,k), n是样本总数，k是降维矩阵中特征维度总数'''
        Z = np.dot(self.X, self.U)
        print('X shape:', np.shape(self.X))
        print('U shape:', np.shape(self.U))
        print('Z shape:', np.shape(Z))
        print('样本矩阵X的降维矩阵Z:\n', Z)
        return Z
         
if __name__=='__main__':
    '10样本3特征的样本集, 行为样例，列为特征维度'
    X = np.array([[10, 15, 29],
                  [15, 46, 13],
                  [23, 21, 30],
                  [11, 9,  35],
                  [42, 45, 11],
                  [9,  48, 5],
                  [11, 21, 14],
                  [8,  5,  15],
                  [11, 12, 21],
                  [21, 20, 25]])
    K = np.shape(X)[1] - 1
    print('样本集(10行3列，10个样例，每个样例3个特征):\n', X)
    pca = CPCA(X,K)

方式三：

import numpy as np
from sklearn.decomposition import PCA
X = np.array([[-1,2,66,-1], [-2,6,58,-1], [-3,8,45,-2], [1,9,36,1], [2,10,62,1], [3,5,83,2]])  #导入数据，维度为4
pca = PCA(n_components=2)   #降到2维
pca.fit(X)                  #训练
newX=pca.fit_transform(X)   #降维后的数据
# PCA(copy=True, n_components=2, whiten=False)
print(pca.explained_variance_ratio_)  #输出贡献率
print(newX)                  #输出降维后的数据

实例练习

在这里插入图片描述

import matplotlib.pyplot as plt
import sklearn.decomposition as dp
from sklearn.datasets.base import load_iris

x,y=load_iris(return_X_y=True) #加载数据，x表示数据集中的属性数据，y表示数据标签
print(x.shape)#显示自变量的形状
print(y.shape)#显示训练目标的形状
# for i in range(2):
#     print(y)
pca=dp.PCA(n_components=2) #加载pca算法，设置降维后主成分数目为2
reduced_x=pca.fit_transform(x) #对原始数据进行降维，保存在reduced_x中
red_x,red_y=[],[]
blue_x,blue_y=[],[]
green_x,green_y=[],[]
for i in range(len(reduced_x)): #按鸢尾花的类别将降维后的数据点保存在不同的表中
    if y[i]==0:
        red_x.append(reduced_x[i][0])
        red_y.append(reduced_x[i][1])
    elif y[i]==1:
        blue_x.append(reduced_x[i][0])
        blue_y.append(reduced_x[i][1])
    else:
        green_x.append(reduced_x[i][0])
        green_y.append(reduced_x[i][1])
plt.scatter(red_x,red_y,c='r',marker='x')
plt.scatter(blue_x,blue_y,c='b',marker='D')
plt.scatter(green_x,green_y,c='g',marker='.')
plt.show()

在这里插入图片描述

学习参考：八斗学院实战教程

pengege666

关注

1
点赞
踩
9

收藏

觉得还不错? 一键收藏
0
评论
计算机视觉基础特征选择和特征提取

文章目录1.特征选择前置知识目的定义操作过程生成过程评价函数停止条件2.特征提取定义与特征选择的区别目的方法3.PCA（主成分分析）介绍步骤具体原理中心化PCA降维协方差矩阵优缺点代码实现部分实例练习1.特征选择前置知识一个对象往往具有很多属性（以下称为特征）(例如：房价的特征可能有地段，面积等一系列属性所影响)•相关特征：对于学习任务（例如分类问题）有帮助，可以提升学习算法的效果；•无关特征：对于我们的算法没有任何帮助，不会给算法的效果带来任何提升；•冗余特征：不会对我们的算法带来新的信息，或
复制链接

扫一扫